
21、(12分)设数列{an}的各项都为正数,且对任意的n∈N+都有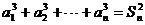 ,其中Sn为数列{an}的前n项和。
,其中Sn为数列{an}的前n项和。
⑴求证: ⑵求数列{an}的通项公式。
⑵求数列{an}的通项公式。
⑶设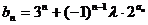 (λ为非零整数,n∈N+)试确定λ的值,使得对任意n∈N+都有bn+1>bn成立。
(λ为非零整数,n∈N+)试确定λ的值,使得对任意n∈N+都有bn+1>bn成立。
20、(12分)某集团准备兴办一所中学, 投资1200万用于硬件建设,为了考虑社会效益和经济利益,对该地区教育市场进行调查,得出一组数据列表(以班为单位)如下
|
|
班级学生数 |
配备教师数 |
硬件建设 |
教师年薪(万元/人) |
|
初中 |
60 |
2.0s |
28 |
1.2 |
|
高中 |
40 |
2.5 |
58 |
1.6 |
根据有关规定,除书本费,办公费外初中生每年可以收取学费600元,高中生每年可以收取学费1500元,因生源和环境等条件限制,办学规模以20至30个班为宜,根据以上情况,请你合理规划办学规模使年利润最大,最大利润为多少万元?(利润=学费收入-年薪支出)
19、(12分)已知函数f(x)=x3-ax2-3x
⑴若f(x)在 上是增函数,求数a的取值范围。
上是增函数,求数a的取值范围。
⑵若方程f(x)=(a2-3)x-1(a>0)至多有两个解,求实数a的取值范围。
18、(12分)函数f(x)的定义域为D:{x|x≠0},且对任意x1,x2∈D,有f(x1x2)=f(x1)+f(x2)
⑴求f(1)的值。 ⑵判断f(x)的奇偶性并证明。
⑶若f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函数,求x 的取值范围。
17、(12分)已知函数f(x)=3cos2x+2cosxsinx+sin2x
⑴求函数y=f(x)的最大值并求最大值时x的值。⑵求函数y=f(x)的单调递增区间。
16、若关于x的不等式(2x-1)2<ax2的解集中的整数恰有2个,则实数a的取值范围是 。
15、已知数列{an}中, ,
,
则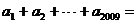 。
。
14、设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若 ,则
,则 。
。
13、ΔABC中,AC=2,BC=3,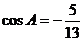 ,则sinB=
。
,则sinB=
。
12、
 设M是ΔABC内一点,且SΔABC的面积为1,定义f(M)=(m,n,p),其中m、n、p分别是ΔMBC,ΔMCA,ΔMAB的面积,若
设M是ΔABC内一点,且SΔABC的面积为1,定义f(M)=(m,n,p),其中m、n、p分别是ΔMBC,ΔMCA,ΔMAB的面积,若 的最小值是( )
的最小值是( )
A、18 B、16 C、9 D、8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com