3、已知命题P：|a|<2，且|b|<1，命题Q：|a-b|<1，命题P是命题Q的

　 (A)充分不必要条件　　　 (B)必要不充分条件

　 (C)充要条件　　　　　 　(D)既不充分又不必要条件

2、已知复数Z满足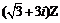=3i，则Z等于

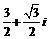　 (A)　　 (B)　　 (C) 　　(D)

1、若全集U={1，2，3，4}，M={1，2}，N={2，3}，则C_U(M∪N)等于

　 (A){1，2，3，}　　　　 (B){2}　　 (C){1，3，4}　　 (D){4}

22．(本小题满分14分)

　　　　 如图，已知直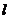线与抛物线相切于点P(2，1)，且与x轴交于点A，O为

坐标原点，定点B的坐标为(2，0)。

　 (1)若动点M满足，求动点M的轨迹C 的方程；

　 (2)若过点B的直线(斜率不等于零)与(1)中的轨迹C交于不同的两点E、F(E在B、F之间)，且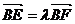，试求λ的取值范围。

21．(本小题满分12分)

设函数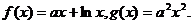

　 (1)当a=-1时，求函数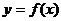图像上的点到直线距离的最小值；

　 (2)是否存在正实数a，使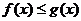对一切正实数x都成立？若存在，求出a的取值范围；若不存在，请说明理由。

20．(本小题满分12分)

　　　 设某企业每月生产电机x台，根据企业月度报表知，每月总产值m(万元)与总支出n(万元)近似地满足下列关系：当时，称不亏损企业，当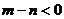时，称亏损企业，且n-m为亏损额。

　 (1)企业要成为不亏损企业，每月至少生产多少台电机？

　 (2)当月总产值为多少时，企业亏损量严重，最大亏损额为多少？

19．(本小题满分12分)

　　　　 已知数列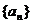是首项为1的等差数列，且，若成等比数列。

　 (1)求数列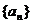的通项公式；

　 (2)设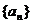的前n项和为，试问当n为何值时，最大？并求出的最大值。

18．(本小题满分12分)

　 　　　　 一个四棱锥的直观图和三视图如图所示：

　 (1)设PB的中点为M，求证：CM//平面PDA；

　 (2)在BC边上是否存在点Q，使得二面角A-PD-Q为120°？若存在，确定点Q的位置；若不存在，请说明理由。

17．(本题满分12分)

已知向量

　 (1)当a//b时，求的值；

　 (2)求上的最大值。

16．在上面体ABCD中，共顶点A的三条棱两两相互垂直，且其长分别为1、、3，若四面体的四个顶点在一个球面上，则这个球的表面积为　　　　　　　 。