2、同学们平时在购买零食时可能会发现，部分食品的外包装上印有“建议零售价”，而实际上我们购买时的价格与其常有较大的差距，这是因为“建议零售价”(　 　)

　 A．是人为定的，而商品的价格由供求关系决定

　 B．高于价值，违背了价值规律

　 C．不能准确地反映供求关系的变化

D．体现了价值决定价格

1、2008年ll月至2009年l0月，受国际金融危机影响，M国流通领域中货币流通次数减少了50%，政府加大宏观调控力度，使流通领域货币量增加了20%。在其他因素不变的情况下，金融危机前售价为20元的商品，在2008年ll月至2009年10月期间的售价应该是(　　 )

A．8元　 　　　B．12元　 　　　C．16元　　　　 D．48元

19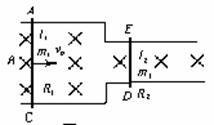．(16分)在如图所示的水平导轨上(摩擦、电阻忽略不计)，有竖直向下的匀强磁场，磁感强度B，导轨左端的间距为L₁=4l₀，右端间距为l₂=l₀。今在导轨上放置ACDE两根导体棒，质量分别为m₁=2m₀，m₂=m₀，电阻R₁=4R0，R₂=R₀。若AC棒以初速度V₀向右运动，求AC棒运动的过程中产生的总焦耳热Q_AC，以及通过它们的总电量q。

[解]由于棒l₁向右运动，回路中产生电流，l_l受安培力的作用后减速，l₂受安培力加速使回路中的电流逐渐减小。只需v₁，v₂满足一定关系，

两棒做匀速运动。

两棒匀速运动时，I=0，即回路的总电动势为零。所以有

Bl_lv₁=Bl₂v₂

再对DE棒应用动量定理B　 l₂·△t=m₂v₂

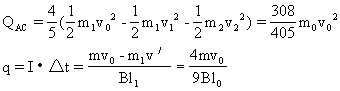
18．(16分)两根金属导轨平行放置在倾角为θ=300的斜面上，导轨左端接有电阻R=10Ω，导轨自身电阻忽略不计。匀强磁场垂直于斜面向上，磁感强度B=0.5T。质量为m=0.1kg ，电阻可不计的金属棒ab静止释放，沿导轨下滑。如图所示，设导轨足够长，导轨宽度L=2m，金属棒ab下滑过程中始终与导轨接触良好，当金属棒下滑h=3m时，速度恰好达到最大速度2m/s，求此过程中电阻中产生的热量？

[解]解：当金属棒速度恰好达到最大速度时，受力分析，

则mgsinθ=F_安+f　　 　3分　　 据法拉第电磁感应定律：E=BLv　　　

据闭合电路欧姆定律：I=　2分　　 ∴F_安=ILB==0.2N　

∴f=mgsinθ－F_安=0.3N　　 2分

下滑过程据动能定理得：mgh－f －W = mv² 　　　　　

解得W=1J ，∴此过程中电阻中产生的热量Q=W=1J　　　　　

17．(15分)如图所示，足够长的光滑金属框竖直放置，框宽l＝0.5 m，框的电阻不计，匀强磁场磁感应强度B＝1 T，方向与框面垂直，金属棒MN的质量为100 g，电阻为1 Ω．现让MN无初速地释放并与框保持接触良好的竖直下落，从释放到达到最大速度的过程中通过棒某一横截面的电量为2 C，求此过程中回路产生的电能．(空气阻力不计，g＝10 m/s²)　

[解]金属棒下落过程做加速度逐渐减小的加速运动，加速度减小到零时速度达到最大，根据平衡条件得

mg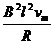＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①　

在下落过程中，金属棒减小的重力势能转化为它的动能和电能E，由能量守恒定律得　

mgh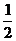＝mv_m²+E　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②　

通过导体某一横截面的电量为　

q＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③　

由①②③解得　

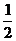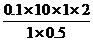E＝mgh－mv_m²＝＝J－J＝3.2 J

16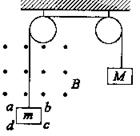．(15分) 正方形金属线框abcd，每边长=0.1m，总质量m=0.1kg，回路总电阻Ω，用细线吊住，线的另一端跨过两个定滑轮，挂着一个质量为M=0.14kg的砝码。线框上方为一磁感应强度B=0.5T的匀强磁场区，如图，线框abcd在砝码M的牵引下做加速运动，当线框上边ab进入磁场后立即做匀速运动。接着线框全部进入磁场后又做加速运动(g=10m/s²)。问：

(1)线框匀速上升的速度多大？此时磁场对线框的作用力多大？

( 2)线框匀速上升过程中，重物M做功多少？其中有多少转变为电能？

[解](1)当线框上边ab进入磁场，线圈中产生感应电流I，由楞次定律可知产生阻碍运动的安培力为F=BIl　　　 由于线框匀速运动，线框受力平衡，F+mg=Mg

　　　　 联立求解，得I=8A　　　 由欧姆定律可得，E=IR=0.16V

　　　　 由公式E=Blv，可求出v=3.2m/s　　 F=BIl=0.4N

(2)重物M下降做的功为W=Mgl=0.14J

　　　　 由能量守恒可得产生的电能为J

15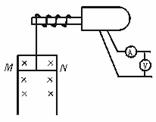．(14分)如图所示，电动机牵引一根原来静止的长L为1 m、质量m为0.1 kg的导体棒MN，其电阻R为1 Ω．导体棒架在处于磁感应强度B为1 T、竖直放置的框架上，当导体棒上升h为3.8 m时获得稳定的速度，导体产生的热量为2 J．电动机牵引棒时，电压表、电流表的读数分别为7 V、1 A．电动机内阻r为1 Ω，不计框架电阻及一切摩擦，g取10 m/s²，求：

[解]．(1)(mg+)v_m＝IU－I²r，v_m＝2m/s(v_m＝－3 m/s舍去)　

(2)(IU－I²r)t＝mgh+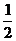mv_m²+Q，t＝1 s　

14．(12分)如图所示，在与水平面成θ角的矩形框范围内有垂直于框架的匀强磁场，磁感应强度为B，框架的ad边和bc边电阻不计，而ab边和cd边电阻均为R，长度均为L，有一质量为m、电阻为2R的金棒MN，无摩擦地冲上框架，上升最大高度为h，在此过程中ab边产生的热量为Q，求在金属棒运动过程中整个电路的最大热功率P_max。

[解]棒MN沿框架向上运动产生感应电动势，相当于电源；ab和cd相当于两个外电阻并联。根据题意可知，ab和cd中的电流相同，MN中的电流是ab中电流的2倍。由焦耳定律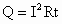知，当ab边产生的热量为Q时，cd边产生的热量也为Q，MN产生的热量则为8Q。金属棒MN沿框架向上运动过程中，能量转化情况是：MN的动能转化为MN的势能和电流通过MN、ab、cd时产生的热量。

设MN的初速度为，由能量守恒得，即

而MN在以速度v上滑时，产生的瞬时感应电动势

所以，整个电路的瞬时热功率为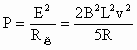

可见，当MN的运动速度v为最大速度时，整个电路的瞬时热功率P为最大值，即

13．(12分) 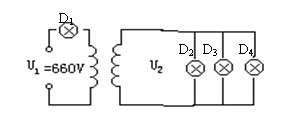如图所示，一个交流高压电源的电压恒为660v，接在变压器上给负载供电。已知变压器副线圈的匝数为n₂＝110匝，灯泡D₁、D₂、D₃、D₄是完全相同的灯泡，其上标有“220v，220W”，1、若起初电路中没有灯泡D₁时，灯泡D₂、D₃、D₄均正常发光，则变压器的原副线圈的匝数比n₁：n₂为多少？原线圈中磁通量变化率的最大值为多少？2、若在原线圈上接上灯泡D₁时，则灯泡D₂的实际功率为多少？(不考虑灯泡电阻随温度的变化)

[解]：(1)n₁:n₂=660:220=3:1　 … … … …　 … …3分

　　　　　　 ∵n₂=110　　　　 … … … …　 … …

∴n₁=330　　　　　　　　　　　 … … … …　 … …2分

由U₁=n₁(ΔΦ/Δt)max　　　 … … … …　 … …2分

∴(Δф/Δt)max=2　　　　　… … … …　 … …2分

(2)R_D=U²/P=220Ω　　　　　　 … … … …　 … …2分

　　 U₁-IR_D=3IR_D　　　　　　　 … … … …　 … …1分

　　 ∴I=660/(4×220)A=3/4A　 … … … …　 … …1分

　　　 P=I²R_D=(3/4)²×220W=123.75W　 … … … …　 … …2分

12．如图所示，矩形单匝线框绕OO′轴在匀强磁场中匀速转动。若磁感应强度增为原来的2倍，则线框转一周产生的热量为原来　　　 倍