21．设函数f(x)＝ln(x+a)+x²+．

　 (Ⅰ)若x＝－1时f(x)取得极值，求a值并讨论f(x)单调性；

　 (Ⅱ)若f(x)存在极值，求a的取值范围，并证明所有极值之和大于ln．

20．平面直角坐标系中，O为坐标系原点，给定两点A(1，0)，B(0，－2)点C满足

　　 ＝α+β，其中α，β∈R，α－2β＝1

　 (Ⅰ)求点C的轨迹方程；

　 (Ⅱ)设点C的轨迹与双曲线(a>0，b>0)交于两点M、N，且以MN为直径的圆过原点．求证：为定值．

19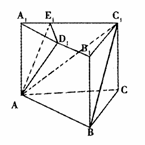．如图，在正三棱柱ABC－A₁B₁C₁中，AB＝AA₁，点D₁是A₁B₁的中点，点E₁在A₁C₁上且D₁E₁⊥A₁E₁．

　 (Ⅰ)证明：平面AD₁E₁⊥平面ACC₁A₁；　　　　　　　　　　　　　　　　　　　　

　 (Ⅱ)求直线AD₁与平面ABC₁所成角的大小．

18．某重点大学自主招生考试，过程依次为自荐材料审查、笔试、面试共三轮进行，规

　　 定：只有通过前一轮考核才能进入下一轮的考核，否则将被淘汰；三轮考核都通过

　　 才算通过该高校的自主招生考试．学生甲三轮考核通过的概率分别为、、，学

　　 生乙三轮考核通过的概率均为，且各轮考核通过与否互独立．

　　 (Ⅰ)求甲没有通过该校自主招生考试的概率;

　　 (Ⅱ)设甲、乙两人中通过该校自主招生考试的人数为ξ，求ξ的分布列与期望．

17．已知函数f(x)＝cos(2x－)+2sin(+x)sin(－x)+1

　　 (Ⅰ)求函数f(x)的最小正周期及图象的对称轴方程；

　　 (Ⅱ)叙述f(x)图象是由g(x)＝sin2x怎样变换得到的?

16．给出下列四个命题：

　 (1)若1<a<b，则<<．

　 (2)圆x²+y²－10x+4y－5＝0上任意一点M关于直线ax－y－5a－2＝0的对称点M′　 也在该圆上．　　

　 (3)若函数y＝f(x－1)的图象关于x＝1对称，则y＝f(x)为偶函数．

　 (4)函数y＝f(1+x)与函数y＝f(1－x)的图象关于直线x＝1对称

　　 其中正确命题的序号为_______________．

15．函数y＝+的最小值是________________．

14．在的展开式中，只有第五项的二项式系数最大，则展开式中的常数项是__________．

13．设x，y满足约束条件若目标函数为Z＝3x+2y，则Z的最大值为___________．

12．已知f(x)是定义在R上，且周期为2的偶函数，当0≤x≤l时，f(x)＝x²，若直线y＝x+a与曲线y＝f(x)恰有两个公共点，那么实数a的值为

　　 A．k(k∈Z)　　　　　　　　　　　 B．2k(k∈Z)

　　 C．2k或2k－(k∈Z)　　　　　　 D．k或k－(k∈Z)

第Ⅱ卷