8.一个氘核()与一个氚核()发生聚变，产生一个中子和一个新核，并出现质量亏损。聚变过程中(　　　 )

　　 A．吸收能量，生成的新核是　　　 B．放出能量，生成的新核是

　 C．吸收能量，生成的新核是　 　　 D．放出能量，生成的新核是

7. 一列简谐横波，在t=1.6 s时刻的图象如下图甲，波上A质点的振动图象如图乙，则( ??)

A．这列波沿x轴正向传播　　　　　　　

　B．这列波的波速是25m/s

C．经过Δt=0.4s，A质点通过的路程是4m　

　 D．质点P将比质点Q先回到平衡位置

6．某人把原来静止于地面上的质量为2kg的物体向上提起1m，并使物体获得1m/s的速度，取g=10m/s²，则这过程中下列说法中正确的是(　　 )

　　 A．人对物体做功21J　　　　　　　　　　　 B．合外力对物体做功1J

　　 C．物体的重力势能增加20J　　 　　　 　　　D．合外力对物体做功21J

5. 如图所示，质量相等的五个物块在光滑水平面上，间隔一定距离排成一条直线。具有初动能E₀的物块1向其它4个静止的物块运动，依次发生碰撞，每次碰撞后不再分开。最后5个物块粘成一个整体。这个整体的动能等于(　　 )

A．E₀　　　　　 B．E₀　　　　

C．E₀　　　　 D．E₀

4．设地球的质量为M，半径为R，自转角速度为，万有引力常量为G，同步卫星离地面的高度为h，表示同步卫星的运行速度有以下几种

　① 　② 　　　　③

　④ 　⑤

　 说法正确的是(　　 )

　　 A．只有①正确，其他均不正确　　　　 B．只有⑤正确，其他均不正确

　　 C．①、②、③、④都正确，⑤不正确　 　D．①、②、③、④、⑤都正确

2.如图所示，一个光滑的小球，放置在墙壁和斜木板之间，当斜木板和竖直 墙壁的夹角θ角缓慢增大时(θ＜90⁰ )，则　 (　　 )

A．墙壁受到的压力减小，木板受到的压力减小

B．墙壁受到的压力增大，木板受到的压力减小

C．墙壁受到的压力增大，木板受到的压力增大

D．墙壁受到的压力减小，木板受到的压力增大

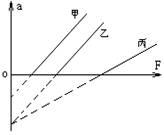_{3.物体A、B、C均静止在同一水平面上，它们的质量分别为m A、m B、m C，与水平面的动摩擦因数分别为μA、μB、μC，用平行于水平面的拉力F分别拉物体A、B、C，所得加速度}a_与拉力F_{的关系图线如图所对应的直线甲、乙、丙所示，甲、乙直线平行，哪些说法正确}(　 )

_{A.μA＜μB　　 m A＝m B　　　　 B.μ B＞μC　　 m B＞m C}

_{C.μB＝μC　　 m B＞m C 　　D.μ A＜μC　 m A＜m C}

1.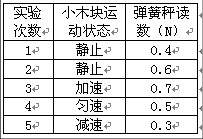在研究摩擦力的实验中，每次用弹簧秤水平拉一放在水平桌面上的木块，木块运动状态及弹簧秤的读数如下表所示(每次木块与桌面的接触面相同)则由表可知 (　 )

A．木块受到的最大摩擦力为0.7N

B．木块受到的最大静摩擦力可能为0.6N

C．在这五次实验中，木块受到的摩擦力大小有三次是相同的

D．在这五次实验中，木块受到的摩擦力大小有二次是相同的

22. (本小题满分10分)

已知为正项数列的前项和，且满足.

(I)求；

(II)求数列的通项公式；

(III)函数，数列的通项公式为

前项和为，若时，不等式恒成立，求实数t的取值范围。

(　 )()

2009-2010学年度第一学期月考(12月)

21.(本小题满分12分)

已知函数，在处取得极值为2。

(I)求函数的解析式；

(II)若函数在区间(m，2m+1)上为增函数，求实数m的取值范围；

(III)若P(x₀，y₀)为图象上的任意一点，直线l与的图象相切于点P，求直线l的斜率的取值范围。

20. (本小题共12分)

已知数列.

(I)求证：{}为等比数列；

(II)记N^*)，T_n为数列{}的前n项和.

　(i)当a=2时，求；

(ii)当时，是否存在正整数m，使得对于任意正整数n都有？　　　　　　 如果存在，求出m的值；如果不存在，请说明理由.