28．数学活动小组接受学校的一项任务：在紧靠围墙的空地上，利用围墙及一段长为60米的木栅栏围成一块生物园地，请设计一个方案使生物园的面积尽可能大。

(1)活动小组提交如图的方案。设靠墙的一边长为 x 米，则不靠墙的一边长为(60－2x)米，面积y= (60－2x) x米²．当x=15时，y_最大值 =450米²。

(2)机灵的小明想：如果改变生物园的形状，围成的面积会更大吗？请你帮小明设计两个方案，要求画出图形，算出面积大小；并找出面积最大的方案．

27．如图，等腰梯形ABCD的边BC在x轴上，点A在y轴的正方向上，A( 0, 6 )，D ( 4，6)，且AB=2.

(1)求点B的坐标；

(2)求经过A、B、D三点的抛物线的解析式；

(3)在(2)中所求的抛物线上是否存在一点P，使得S_△PBD=S_梯形ABCD。若存在，请求出该点坐标，若不存在，请说明理由.

26．已知抛物线y=(1-m)x²+4x-3开口向下，与x轴交于A(x₁,0)和B(x₂,0)两点，其中x_l<x₂．

(1)求m的取值范围；

(2)若x₁²+ x₂²=10，求抛物线的解析式，并在给出的直角坐标系中画出这条抛物线；

25.已知直线y＝－2x+b(b≠0)与x轴交于点A，与y轴交于点B;一抛物线的解析式为y＝x²－(b+10)x+c.

⑴若该抛物线过点B，且它的顶点P在直线y＝－2x+b上，试确定这条抛物线的解析式；

⑵过点B作直线BC⊥AB交x轴于点C，若抛物线的对称轴恰好过C点，试确定直线y＝－2x+b的解析式.

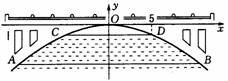
24．如图，有一座抛物线型拱桥，在正常水位时水面AB的宽是20米，如果水位上升3米时，水面CD的宽为10米，

(1)建立如图所示的直角坐标系，求此抛物线的解析式；

(2)现有一辆载有救援物质的货车从甲地出发，要经过此桥开往乙地，已知甲地到此桥千米，(桥长忽略不计)货车以每小时40千米的速度开往乙地，当行驶到1小时时，忽然接到紧急通知，前方连降大雨，造成水位以每小时米的速度持续上涨，(货车接到通知时水位在CD处)，当水位达到桥拱最高点O时，禁止车辆通行；试问：汽车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过多少千米？

23．某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程．下面的二次函数图像(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系)．

　根据图像提供的信息，解答下列问题：

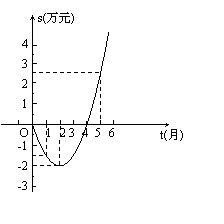　(1)求累积利润s(万元)与时间t(月)之间的函数关系式；

　(2)求截止到几月末公司累积利润可达到30万元；

　(3)求第8个月公司所获利润是多少万元？

22．华联商场以每件30元购进一种商品，试销中发现每天的销售量(件)与每件的销售价(元)满足一次函数y=162－3x；

(1)写出商场每天的销售利润(元)与每件的销售价(元)的函数关系式；

(2)如果商场要想获得最大利润，每件商品的销售价定为多少为最合适？最大销售利润为多少？

21. 已知抛物线y=ax²+bx+c经过A(－1,0)、B(3,0)、C(0,3)三点，

(1)求抛物线的解析式和顶点M的坐标，并在给定的直角坐标系中画出这条抛物线。

(2)若点(x₀,y₀)在抛物线上，且0≤x₀≤4,试写出y₀的取值范围。

20．二次函数y=x²－2x－3与x轴两交点之间的距离为_________.

19．抛物线y=(x－1)²+3的顶点坐标是____________．