4．[答案]BD

[解析]电场力的方向与面ABCD垂直，所以面ABCD是等势面，A、D两点的电势差为0，又因A、A两点的电势差不为0，所以选项A错。带正电的粒子从A点到D电场力不做功，而由D→D＇电场力做功，所以选项B正确；同理，带负电的粒子从A点沿路径A→D→D＇移到D＇点，电场力做负功，电势能增大，选项C错；由电场力做功的特点得选项D也正确。

3．[答案]B

[解析]从无穷远处电势为零开始到r = r₂位置，势能恒定为零，在r = r₂到r = r₁过程中，恒定引力做正功，势能逐渐均匀减小，即势能为负值且越来越小，此部分图像为A、B选项中所示；r ＜ r₁之后势能不变，恒定为－U₀，由引力做功等于势能将少量，故U₀=F₀(r₂－r₁)．所以选项B正确

2．[答案]A

[解析]本题属于连接体问题，主要考查牛顿第二定律在电场中的应用，设加速度为a，对整体有：，再隔离球2分析：，联立两式得：，所以选项A正确

1．[答案]BD

[解析]电场是矢量，叠加遵循平行四边行定则，由和几何关系可以得出，A错B对。在之间，合场强的方向向左，把负电荷从O移动到C，电场力做负功，电势能增加，C错D对。

16．如图35所示，一根长 L = 1.5m 的光滑绝缘细直杆MN ，竖直固定在场强为 E ==1.0 ×10⁵N / C 、与水平方向成θ＝30⁰角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球 A ，电荷量Q＝+4.5×10^－6C；另一带电小球 B 穿在杆上可自由滑动，

电荷量q＝+1.0 ×10^{一6 C}，质量m＝1.0×10^{一2 kg} 。现将小

球B从杆的上端N静止释放，小球B开始运动。(静电力常量

k＝9.0×10 ⁹N·m²／C²，取 g =l0m / s₂)

(1)小球B开始运动时的加速度为多大？

(2)小球B 的速度最大时，距 M 端的高度 h₁为多大？

(3)小球 B 从 N 端运动到距 M 端的高度 h₂＝0.6l m 时，

速度为v＝1.0m / s ，求此过程中小球 B 的电势能改变了多少？　　　　 图35

答案及解析

15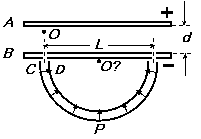．如图23所示，A、B为两块平行金属板，A板带正电、B板带负电。两板之间存在着匀强电场，两板间距为d、电势差为U，在B板上开有两个间距为L的小孔。C、D为两块同心半圆形金属板，圆心都在贴近B板的O’处，C带正电、D带负电。两板间的距离很近，两板末端的中心线正对着B板上的小孔，两板间的电场强度可认为大小处处相等，方向都指向O’。半圆形金属板两端与B板的间隙可忽略不计。现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒(微粒的重力不计)，问：　　　　　　　 图23

(1)微粒穿过B板小孔时的速度多大；

(2)为了使微粒能在CD板间运动而不碰板，CD板间的电场强度大小应满足什么条件；

(3)从释放微粒开始，经过多长时间微粒会通过半圆形金属板间的最低点P

14．如图10(a)所示，在光滑绝缘水平面的AB区域内存在水平向左的电场，电场强度E随时间的变化如图10(b)所示。不带电的绝缘小球P₂静止在O点。t=0时，带正电的小球P₁以速度v₀从A点进入AB区域。随后与P₂发生正碰后反弹，反弹速度是碰前的倍。P₁的质量为m₁，带电量为q，P₂的质量为m₂=5m₁，A、O间距为L₀，O、B间距为.已知，.

(1)求碰撞后小球P₁向左运动的最大距离及所需时间。

(2)讨论两球能否在OB区间内再次发生碰撞。

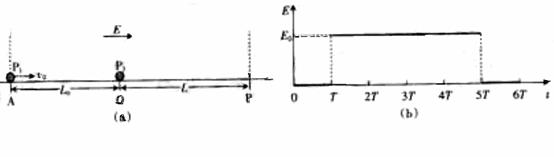
　　　　　　　　　　　　　　　　　　 图10

12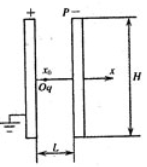．带等量异种电荷的两平行金属板相距L，板长H，竖直放置，x轴从极板中点O通过，如图20所示。板间匀强电场的场强为E，且带正电的极板接地。将一质量为m、电量为+q的粒子(重力不计)从坐标为x₀处释放。

　 　　 (1)试从牛顿第二定律出发，证明该带电粒子在极板间运动的过程中，电势能与动能总和保持不变。

(2)为使该粒子从负极板上方边缘的P点射出，须在x₀处使该粒子获得竖直向上的初速度v₀为多大?　　　　　　　　　　　　　　　　　　　 图20

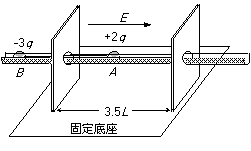　13．如图33所示，沿水平方向放置一条平直光滑槽，它垂直穿过开有小孔的两平行薄板，板相距3.5L。槽内有两个质量均为m的小球A和B，

球A带电量为+2q，球B带电量为-3q，两球由长为

2L的轻杆相连，组成一带电系统。最初A和B分别

静止于左板的两侧，离板的距离均为L。若视小球

为质点，不计轻杆的质量，在两板间加上与槽平行　　　　　　 图33

向右的匀强电场E后(设槽和轻杆由特殊绝缘材料

制成，不影响电场的分布)，求：　　　　　　　　　　　　　　

(1)球B刚进入电场时，带电系统的速度大小；

(2)带电系统从开始运动到速度第一次为零所需的时间及球A相对右板的位置。

11．如图9所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内，存在两个场强大小均为E的匀强电场I和II，两电场的边界均是边长为L的正方形(不计电子所受重力)。　　　　　　　　　　　　　　　　　　　　　　

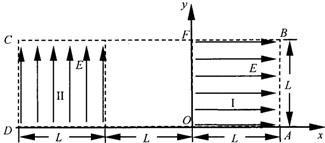(1)在该区域AB边的中点处由静止释放电子，　　

求电子离开ABCD区域的位置。

(2)在电场I区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置。

(3)若将左侧电场II整体水平向右移动L/n(n≥1)，　　　　　　 图9

仍使电子从ABCD区域左下角D处离开(D不随电场移动)，求在电场I区域内由静止释放电子的所有位置。

10．a、b、c、d是匀强电场中的四个点，它们正好是一个矩形的四个顶点。电场线与矩形所在的平面平行。已知a点的电势是20V，b点的电势是24V，d点的电势是4V，如图30所示。　 由此可知，c点的电势为(　　 )　　　　　　　　　　　　　　　　　　 图30

A、4V　　　 B、8V　　　 C、12V　　　 D、24V