
20.(本题满分12分)
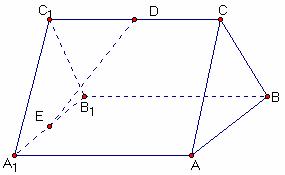
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.
( Ⅰ)求证:AB⊥DE;(Ⅱ)求三棱锥
Ⅰ)求证:AB⊥DE;(Ⅱ)求三棱锥 的体积,并求直线A1B1到与它平行的平面DAB的距离。
的体积,并求直线A1B1到与它平行的平面DAB的距离。
19.(本题满分12分)某造船公司年最高造船量是20艘. 已知造船x艘的产值函数R (x)=3700x + 45x2 – 10x3(单位:万元),成本函数为C(x)=460 x +5000(单位:万元).又在经济学中,函数f(x)的边际函数Mf(x)定义为:Mf(x)= f(x+1)-f(x).求:
(1 )利润函数P(x)及边际利润函数MP(x);(提示:利润=产值-成本)
)利润函数P(x)及边际利润函数MP(x);(提示:利润=产值-成本)
(2)年造船量安排多少艘时, 可使公司造船的年利润最大?
(3)求边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
18、某教研机构准备举行一次高中数学新课程研讨会,拟邀请50名使用不同版本的一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大 版 版 |
|
人数 |
20 |
15 |
10 |
5 |
(1)假设使用北师大版的5名教师中有3名男教师,2名女教师,若随机选出2名用北师大版的教师发言,求恰好是一男一女的概率P
(2)从这50名教师中随机选出2名教师发言,求第一位发 言的教师所使用版本是北师大版的概率P
言的教师所使用版本是北师大版的概率P
16.若曲线y=f(x)上存在三点A、B、C,使 ,则称点曲线有“中位点”,下列曲线:①y=cosx,
,则称点曲线有“中位点”,下列曲线:①y=cosx,
② ,③
,③ ,④y=cosx+x2,⑤
,④y=cosx+x2,⑤ ,有“中位点”的有
,有“中位点”的有
(写出所有满足要求的序号)
|
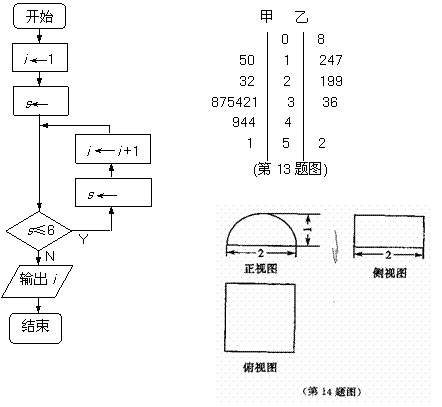
15.已知某个几何体的三视图如图(正视图中的弧线是半圆),根据图中标出的尺寸(单位:㎝),
可得这个几何体的表面积是 cm2。
14. 根据如图所示的算法流程图,可知输出的结果 为_______________.
为_______________.
13.如图是甲乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的是________运动员.
12.设函数f是定义在正整数有序对的集合上,并满足:①
② ③
③ 则
则 +
+ 的值是
(
)
的值是
(
)
A. 96 B. 64  C. 48 D. 24
C. 48 D. 24
10.已知条件p: k= ,条件q:直线y=kx+2与圆x2+y2=1相切,则p是q的 ( )
,条件q:直线y=kx+2与圆x2+y2=1相切,则p是q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
|
 则方程f(x)=2的实数根的个数是 ( )
则方程f(x)=2的实数根的个数是 ( )
A 0 B 1 C 2 D 3
9.已知函数 的值域为( )
的值域为( )
A.  B.
B.  C.
C.  D..
D.. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com