22．(本小题满分14分)若存在实常数和，使得函数和对其定义域上的任意实数分别满足：和，则称直线为和的“隔离直线”．已知，(其中为自然对数的底数)．

(1)求的极值；

(2) 函数和是否存在隔离直线？若存在，求出此隔离直线方程；若不存在，请说明理由．

福建省泉州七中2010届高三上学期第三次月考

21.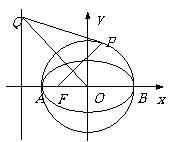 (本小题满分12分)已知圆:交轴于A,B两点,曲线是以AB为长轴,离心率为的椭圆,其左焦点为F,若P是圆上一点,连结PF,过原点作直线PF的垂线交直线x=-2于点Q.

(Ⅰ)求椭圆的标准方程；

(Ⅱ) 当点P在圆上运动时(不与A、B重合),求证:直线PQ与圆相切.

19．(本小题满分12分)已知正项数列前n项和为，首项为，且成等差数列。

(1)求数列的通项公式；(2)若，为数列的前n项和，证明。

20(本小题满分12分)．

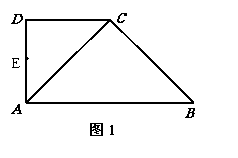
如图1，在直角梯形中, 将 沿折起,使平面ADC平面ABC,得到几何体D－ABC, 如图2所示.

　 (Ⅰ)若E为AD的中点，试在线段CD上找一点F，使EF∥平面ABC，并加以证明；

　 (Ⅱ)求证: BC⊥平面ACD；

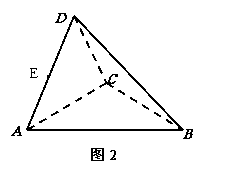　 (Ⅲ)求几何体A－BCD的体积.

18. (本小题满分12分)为了在如图所示的直河道旁建造一个面积为5000m²的矩形堆物场，需砌三面砖墙BC、CD、DE，出于安全原因，沿着河道两边需向外各砌10m长的防护砖墙AB、EF，若当BC的长为m时，所砌砖墙的总长度为m，且在计算时，不计砖墙的厚度，求

(1)y关于x的函数解析式y=f(x);

(2)若BC的长不得超过40m，则当BC为何值时，y有最　　

小值，并求出这个最小值.

17、(本小题满分12分)在中，角、、的对边分别为、、，且，．　　 (Ⅰ)求角；　 (Ⅱ)设，求边的大小．

16．给出下列四个命题：

①设，则的充要条件是且；

②任意的锐角三角形中，有成立；

③平面上n个圆最多将平面分成个部分；

④空间中直角在一个平面上的正投影可以是钝角．

其中真命题的序号是　　　　　　　　　　　 (要求写出所有真命题的序号)．

15．过椭圆的右焦点作一条斜率为2的直线与椭圆交于两点，为坐标原点，则的面积为　　　　 ．

14、已知等差数列的首项为24，公差为，则当n=　　　　 时，该数列的前n项和取得最大值。

13．已知对于任意实数，函数满足. 若方程有2009个实数解，

　 则这2009个实数解之和为 　　　　　　　.

12.设是定义在上的恒不为零的函数，对任意的实数，都有，若，，则数列的前项和的取值范围是(　 )

A．　　　　 B. 　　　　　C. 　　　　D.

第二卷　 (非选择题　 满分90分)