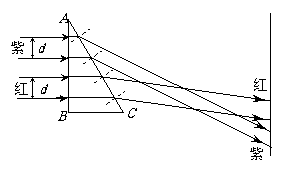
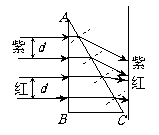
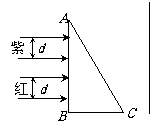
19、如图所示，截面为ABC的玻璃直角三棱镜放置在空气中，宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB，在三棱镜的另一侧放置一平行于AB边的光屏，屏的距离远近可调，在屏上出现紫、红两条光带，可能是

A．红色光带在上，紫色光带在下，红色光带较宽

B．红色光带在下，紫色光带在上，红色光带较宽

C．紫色光带在上，红色光带在下，紫色光带较宽

D．紫色光带在下，红色光带在上，紫色光带较宽

答案：AB

由和知，作出下列两种情况的光路图。

18、如图所示，质量为m的球置于斜面上，被一个竖直挡板挡住。现有一个力F拉斜面，使斜面在水平面上做加速度为a的匀加速直线运动，忽略一切摩擦，以下说法中正确的是

A．若加速度足够小，竖直挡板对球的弹力可能为零

B．若加速度足够大，斜面对球的弹力可能为零

C．斜面和挡板对球的弹力的合力等于ma

D．斜面对球的弹力不仅有，而且是一个定值

答案：D

对球：

17、如图所示，在光滑的水平面上，一质量为m，半径为r，电阻为R的均匀金属环，以v0的初速度向一磁感应强度为B的有界匀强磁场滑去(磁场宽度d>2r)。圆环的一半进入磁场历时t秒，这时圆环上产生的焦耳热为Q，则t秒末圆环中感应电流的瞬时功率为

A.

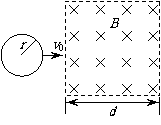B.

C. 　

D. 　

答案：B

t秒末圆环中感应电动势为

由能量守恒知，减少的动能全部转化为焦耳热：

t秒末圆环中感应电流的功率为

16、图示为一个内、外半径分别为R1和R2的圆环状均匀带电平面，其单位面积带电量为。取环面中心O为原点，以垂直于环面的轴线为x轴。设轴上任意点P到O点的的距离为x，P点电场强度的大小为E。下面给出E的四个表达式(式中k为静电力常量)，其中只有一个是合理的。你可能不会求解此处的场强E，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断。根据你的判断，E的合理表达式应为

A.　

B.

C.　 　

D.

答案：A　09北京　 微元法、对称性的应用。 　

圆环电荷在x轴上激发的场强一定是沿着x轴方向，且为每部分场强在x轴上分量相加，而y轴上的分量则因对称关系而相互抵消为零。

空心均匀带电圆环在P点激发的场强E等于半径为R2的实心均匀带电圆面在P点激发的场强E1与放在关于P点对称的半径为R1的实心均匀带电圆面在P点激发的场强E2之差，即E=E1-E2。所以场强式中应该出现相减的关系式，于是选项C、D被排除。　　　

当R1=0时，此时带电圆环演变为带电圆面。对于B选项而言：当R1=0时，E<0沿x轴负向(设σ为正)。实际上E＞0沿x轴正向(设σ为正)，所以B选项错误。

15、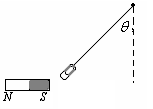如图所示，质量为m的回形针系在细线下端被磁铁吸引保持静止，此时细绳与竖直方向的夹角为，则下列说法中正确的是

A．回形针平衡时受到磁体对它的磁力和绳的拉力作用，两力　　

合力的方向向上偏右

B．回形针平衡时受到磁体对它的磁力和绳的拉力作用，两力

合力的方向向上偏左

C．现用点燃的火柴对回形针加热，细绳与竖直方向的夹角减　

小，原因是回形针加热后，分子电流排列无序了

D．现用点燃的火柴对回形针加热，细绳与竖直方向的夹角为减小，原因是回形针加

热后，分子电流消失了

答案：C　

回形针平衡时受到磁体对它的磁力和绳的拉力作用，两力合力与重力平衡，所以方向竖直向上，AB项错误；用点燃的火柴对回形针加热，回形针磁性会减弱是因为分子电流排列无序了，所以C项正确。

14、下列说法正确的是

A.太阳辐射的能量主要来自太阳内部的裂变反应

B.卢瑟福的粒子散射实验可以估测原子核的大小

C.大量氢原子从n=4的激发态跃迁到n=2的激发态时，可以产生4种不同频率的光子

D.当铀块的体积小于临界体积时就会发生链式反应，瞬时放出巨大能量

答案：B　

太阳辐射的能量主要来自太阳内部的聚变反应；大量氢原子从n=4的激发态跃迁到n=2的激发态时，可以产生2种不同频率的光子；发生链式反应时，铀块的体积必须大于临界体积。

22.(本小题满分14分)

已知函数f(x)是y=－1(x∈R)的反函数，函数g(x)的图象与函数y=的图象关于直线y=x－1成轴对称图形，记 F(x)=f(x)+g(x).

(1)求函数F(x)的解析式及定义域;

(2)试问在函数F(x)的图象上是否存在两个不同的点A，B，使直线AB恰好与y轴垂直.若存在，求出A，B坐标;若不存在，说明理由.

21.(本小题满分12分)

对于抛物线y=x²和实数k(k≠0)，

(1)求证:存在1条不过原点，斜率为k的直线l和1个圆心在原点的圆O，使它们满足: l交圆O于A、C两点，交y=x²于B、D两点，且B是线段AC的中点， C是BD的中点;

(2)当(1)中的k值变化时，求点C纵坐标的最小值.

20.(本小题满分12分)

市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析，发现有如下规律:该商品的价格每上涨 x%(x＞0)，销售数量就减少kx% (其中k为正常数).目前，该商品定价为a元， 统计其销售数量为b个.

(1)当k=时，该商品的价格上涨多少，就能使销售的总金额达到最大？

(2)在适当的涨价过程中，求使销售总金额不断增加时k的取值范围.

18.(本小题满分12分)

已知由正数组成的等比数列{a_n}，若前2n项之和等于它前2n项中的偶数项之和的11倍，第3项与第4项之和为第2项与第4项之积的11倍，求数列{a_n}的通项公式.

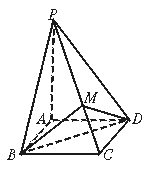
19_.(本小题满分12分)

如图，四棱锥P－ABCD的底面ABCD是正方形，侧棱PA⊥底面ABCD，M是侧棱PC上一点，且BM⊥PC.

(1)求证: PC⊥平面BMD；

(2)若二面角B－PC－D的大小为120°，求二面角A－BD－M的大小.