
(17) (满分8分)已知随机变量 x 的分布列如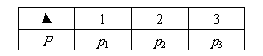 下,且已知 Ex = 2,Dx = 0.5,
下,且已知 Ex = 2,Dx = 0.5,
求:
(I) p1、p2、p3
(II) P(-1 < x < 2)、P(1 < x < 2)
(18) (满分10分)设数列 是等比数列,
是等比数列, ,公比
,公比 是
是 的展开式中的第二项(按
的展开式中的第二项(按 的降幂排列).
的降幂排列).
(1)求常数 与
与 的值;
的值;
(2)用 ,
, 表示数列{
表示数列{ }的前项和
}的前项和 ;
;
(3)若 ,用
,用 ,
, 表示
表示 .
.
(19) (满分10分)某保险公司开设了一项保险业务,若在一年内事件 E 发生,该公司要赔偿10000 元,设一年内 E 发生的概率为 0.001,要使公司收益的期望值为 500 元,公司应要求顾客交多少保险金?
(20)(满分12分)将15名转学生(12位男生3位女生)平均分到高三级甲、乙、丙三个班.
(I) 每班各分配到一名女生的概率是多少?
(II) 3名女生同去一个班的概率是多少?
 (13) 为获知野生动物保护区内某种野生动物的数量,工作人员逮到该种动物1200只,作标记后放回. 若干天后,再逮到该种动物1000只,数得当中有100只作过标记. 按概率方法估算,保护区内这种动物有 只.
(13) 为获知野生动物保护区内某种野生动物的数量,工作人员逮到该种动物1200只,作标记后放回. 若干天后,再逮到该种动物1000只,数得当中有100只作过标记. 按概率方法估算,保护区内这种动物有 只.
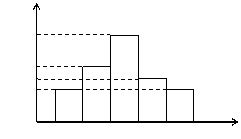
(14) 某电子元件厂对一批新产品的使用寿命进行检
验,质检科抽取了一个容量为100的样本,经
检测统计后,绘制出了该产品使用寿命的频率
分布直方图(如图),估计这批新产品的使用
寿命在400h以上的概率是 .
(15) 设 (+x) 10 = a0 + a1 x + a2 x 2 + … + a10 x 10,则 (a0 + a2 + a4 + … + a10) 2-(a1 + a3 + a5 + … + a9) 2 的值为 .
(16) 三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为凹数,如524,746等,那么各位上无重复数字的三位凹数共有 个.
(1)已知随机变量 x 服从二项分布,且 ,
, ,则二项分布的参数
,则二项分布的参数 的值为
的值为
(A) (B)
(B)  (C)
(C)  (D)
(D)

(2)对总数为N的一批零件抽取一个容量为30的样本,若每个零件被抽到的概率为0.25,则N的值为
(A) 100 (B) 120 (C) 150 (D) 200
(3)10张奖券中有2张是有奖的,甲、乙两人中各抽1张,甲先抽,然后乙抽,设甲中奖的概率为p1,乙中奖的概率为p2,那么
(A) p1 > p2 (B) p1 < p2 (C) p1 = p2 (D) p1, p2大小不确定
(4)若x Î N,且x<55,则(55-x)(56-x)…(68-x)(69-x)=
(A) A (B) A (C) A (D) A
(5)学校黑板报设有9个学科专栏,由高中三个年级各负责3个专栏,其中数学由高三级负责. 则不同的分工方法种数为
(A) 1680 (B) 560 (C) 280 (D) 140
(6)某年级8个班协商组建年级篮球队,共需10名队员,每个班至少有1个名额,不同的名额分配方案种数为
(A) 16 (B) 24 (C) 28 (D) 36
(7)把红、黄、绿、蓝四张纸牌随机分发给甲、乙、丙、丁四个人,每人分得一个. 事件“甲分得红牌”与事件“乙分得红牌”是 (A) 对立事件 (B) 不可能事件
(C) 互斥但非对立事件 (D) 以上答案均不对
(8)氨基酸的排列顺序是决定蛋白质多样性的原因之一,某肽链由7种不同的氨基酸构成,研究人员试验每次改变其中三种氨基酸的位置,其他四种位置不变,则试验的总次数为
(A) 126 (B) 70 (C) 35 (D)210
(9)将两名男生、五名女生的照片排成一排贴在光荣榜上,恰有三名女生的照片贴在两名男生的照片之间的概率为
(A) (B) (C) (D)
(10)3位好友不约而同乘一列火车. 该列火车有10节车厢,那么至少有2人在同一节车厢相遇的概率为
(A) (B) (C) (D)
(11)设随机变量ξ的概率分布列为 ,其中c为常数,则
,其中c为常数,则 的值为
的值为
(A) (B)
(B) (C)
(C) (D)
(D)
(12)某仪表显示屏上有一排7个小孔,每个小孔可显示出0或1,若每次显示其中三个小孔,且相邻的两个小孔不能同时显示,则这个显示屏可以显示不同信号的种数为
(A) 10 (B) 48 (C) 60 (D) 80
(17)(本小题满分8分)
平行四边形ABCD中,已知: ,
, , 求证:A、E、F三点共线。
, 求证:A、E、F三点共线。

(18)(本小题满分10分)
已知△ABC的顶点坐标为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在边AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.

(19)(本小题满分10分)在正方体 中,E、F、G、H为
中,E、F、G、H为 、
、 、
、 、
、 中点.
中点.
 (Ⅰ)求证:
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: //平面
//平面 。
。
(20)(本小题满分12分)
已知 为直角梯形,
为直角梯形, //
// ,
, ,
,  ,
,  ,
,  平面
平面 ,
,
(Ⅰ)若异面直线 与
与 所成的角为
所成的角为 ,且
,且 ,求
,求 ;
;
(Ⅱ)在(Ⅰ)的条件下,设 为
为 的中点,能否在
的中点,能否在 上找到一点
上找到一点 ,使
,使 ?
?
(Ⅲ)在(Ⅱ)的条件下,求二面角 的大小.
的大小.

(13) 是球
是球 面上的四个点,
面上的四个点, 两两垂直,且
两两垂直,且 ,则球的体积为__________.
,则球的体积为__________.
(14)设 ,
, ,则
,则
(15)已知: 与
与 的夹角为45°,要使
的夹角为45°,要使 与
与 垂直,则
垂直,则 =
.
=
.
(16)向量的命题:①若非零向量 ,向量
,向量 ,则
,则 ;②四边形ABCD是菱形的充要条件是
;②四边形ABCD是菱形的充要条件是 且
且 ;③若点G是
;③若点G是 的重心,则
的重心,则 ④
④ 中,
中, 和
和 的夹角为
的夹角为 ,其中正确的命题序号是
__________.
,其中正确的命题序号是
__________.
(1)已知向量 的夹角为
的夹角为
(A)0° (B)45°
(C)90° (D)180°
(2)在空间四边形ABCD中,AB=BC,AD=DC,则对角线AC与BD所成角的大小是
(A)90° (B)60° (C)45° (D)30°
(3)将函数 的图象按向量
的图象按向量 平移后所得图象的函数解析式为
平移后所得图象的函数解析式为
(A) (B)
(B) (C)
(C) (D)
(D)
(4)已知 ,
, ,若
,若 ,则
,则 与
与 的值分别为
的值分别为
(A)-5,-2 (B)5,2
(C) (D)
(D)
(5)若向量 、
、 的坐标满足
的坐标满足 ,
, ,则
,则 ·
· 等于
等于
(A) (B)
(B) (C)
(C) (D)
(D)
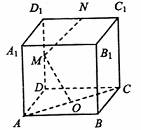 (6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
(6)在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别
是棱DD1、D1C1的中点,则直线OM
(A)是AC和MN的公垂线
(B)垂直于AC,但不垂直于MN
(C)垂直于MN,但不垂直于AC
(D)与AC、MN都不垂直
(7)地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的球面距离为(地球半径为R)
(A)R (B) (C)
(C) (D)
(D)
(8)如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为
 (A)61cm
(B)
(A)61cm
(B) cm
cm
(C) cm (D)
cm (D) cm
cm
(9)在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
(A) (B)
(B) (C)
(C) (D)
(D)
(10)平面内有 且
且 ,则
,则 一定是
一定是
(A)钝角三角形 (B)直角三角形
(C)等腰三角形 (D)等边三角形
(11)在棱长为2的正方体AC1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离是
(A) (B)
(B) (C)
(C) (D)
(D)
(12)设PA,PB,PC是从点P引出的三条射线,每两条的夹角都等于60°,则直线PC与平面APB所成角的余弦值是
(A) (B)
(B) (C)
(C) (D)
(D)
(17)(本小题满分8分)
已知直线l垂直于直线3x + 2y-6 = 0,且在两坐标轴上的截距之和为-2,求直线l的方程。
(18)(本小题满分10分)
直线l过点(1,0),且被两平行直线3x + y-6 = 0和3x + y + 3 = 0所截得的线段长为9,求直线l的方程。
(19)(本小题满分10分)
已知直线l1:5x-2y + 3m(3m + 1) = 0与l2:2x + 6y-3m(9m +20) = 0。当m为何值时,两直线l1,l2的交点到直线4x-3y-12 = 0的距离最小?最小值为多少?
(20) (本小题满分12分)
已知已知过点A(1,1)且斜率为-m(m>0)的直线l与x,y轴分别交于P,Q,过P,Q作直线2x + y = 0的垂线,垂足为R,S.求四边形PRSQ的面积的最小值。
(13)直线l1与l2的斜率是方程6x2 + x-1 = 0的两根,则直线l1和l2的夹角是 .
(14)若直线l1:ax + 2y + 6 = 0与直线l2:x + (a-1)y + a2-1 = 0,则l1∥l2时,a =
l1⊥l2时,a = .
(15) 直线l1:bx-2y + 2 = 0和直线l2:2x + 6y + c = 0相交于点(1,m),且l1到l2的角为 ,则b,c,m的值分别为
.
,则b,c,m的值分别为
.
(16)直线l1过点P1(4,2),直线l2过点P2(-1,3),若l1∥l2,且l1与l2间距离最大,此时l1的方程是 .
(1)下列命题不正确的是
A、若直线l1∥l2,则k1 = k2 B、若直线l1⊥l2,则k1·k2 =-1
C、若k1 = k2,则l1∥l2 D、若k1·k2 =-1,则l1⊥l2
(2)直线l1:2x + (m + 1)y + 4 = 0与直线l2:mx + 3y-2 = 0平行,则m的值为
A、2 B、-3 C、2或-3 D、-2或-3
(3)已知直线3ax-y = 1与直线 垂直,则a的值为
垂直,则a的值为
A、-1或 B、1或
B、1或 C、-
C、- 或-1 D、-
或-1 D、- 或1
或1
(4)以A(1,-1),B(-2,0)为端点的线段的垂直平分线的方程是
A、3x + y-4 = 0 B、3x + y + 4 = 0
C、3x-y + 1 = 0 D、3x-y -1 = 0
(5)直线x + y-1 = 0到直线x·sin 的角是
的角是
A、 B、
B、 C、
C、 D、
D、
(6)已知直线l1:
A、 B、
B、 或0 C、
或0 C、 或
或 D、
D、 或
或 或0
或0
(7)在直线l:3x-4y-27 = 0上到点P(2,1)距离最近的点的坐标是
A、(5,-3) B、(9,0) C、 D、(-5,3)
(8)m,n R,直线
R,直线 过定点
过定点
A、(-1,3) B、 C、
C、 D、
D、
(9已知直线mx + 4y-2 = 0与2x-5y + n = 0垂直,垂足为(1,P),则m-n + p的值为
A、24 B、20 C、0 D、-4
(10)点(0,2)关于直线x + 2y-1 = 0的对称点是
A、(-2,0) B、(,0) C、(0,-1)
D、
(11)若点(4,a)到直线4x-3y = 1的距离不大于3,则a的取值范围是
A、[0,10] B、(0,10) C、 D、
D、
(12)入射光线在直线l1:2x-y-3 = 0上,经过x轴反射,反射光线在直线l2上,再经过y轴反射到直线l3上,则直线l3的方程为
A、x-2y + 3 = 0 B、2x-y + 3 = 0 C、2x + y-3 = 0 D、2x-y + 6 = 0
当 时,
时, ∴
∴ 
 ∴
∴ ∴
∴
当 时,
时, ∴
∴ ∴ -1≤m<0.
∴ -1≤m<0.
当 时,
时,
综合得:
(18).⑴ ,故f(x)的定义域为(-1,0)∪(0,1).
,故f(x)的定义域为(-1,0)∪(0,1).
⑵ ∵ , ∴f(x)是奇函数。
, ∴f(x)是奇函数。
⑶ 设0<x1<x2<1,则

∵ 0<x1<x2<1, ∴x2-x1>0, x1x2>0,

∴  ,
,
∴ , 即
, 即 ∴
∴ 在(0,1)内递减。
在(0,1)内递减。
另解: ∴当x∈(0,1)时,
∴当x∈(0,1)时,
故 在
在 内是减函数。
内是减函数。
(19).设生产x吨产品,利润为y元,则


∴ 当 时,
时, (元) 答:略。
(元) 答:略。
(20)(Ⅰ)令x-2=t,则x=t+2.
由于 ,
,
所以 
∴ 
∵  的图象关于y轴对称 ∴
的图象关于y轴对称 ∴  且
且  ,即
,即
故 
(Ⅱ)

设存在 ,使F(x)满足题目要求,则当-∞<x1<x2≤-3时,F(x)是减函数,即
,使F(x)满足题目要求,则当-∞<x1<x2≤-3时,F(x)是减函数,即

由假设-x1>-x2≥3>0, ∴ 
∴  … … … … … ①
… … … … … ①
又  ∴
∴ 
∴ 
要使①式恒成立,只须 ≥0 即
≥0 即 ≤
≤
又当 时,F(x)是增函数,
时,F(x)是增函数,
即 F(x1)-F(x2)<0,也就是 … … ②
… … ②
此时 
 ,
, 
要使②式恒成立,只须  ≤0 即
≤0 即  ≥
≥
故存在 =
= 满足题目要求。
满足题目要求。
另解: 依题意F(-3)是F(x)的极小值, ∴  .
.
∵  , ∴
, ∴  ,
,
即 . 当
. 当 =
= 时,
时, ,
, 
∴当 时,
时, 在
在 上是减函数;
上是减函数;
当 时,
时, 是增函数。
是增函数。
故存在 满足题目要求。
满足题目要求。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com