2．有一条多肽链，分子式为CxHyOpNqS，将它彻底水解后，只得到下列四种氨基酸。分析推算已知水解得到的氨基酸个数为q-2，则该肽链中含有赖氨酸的数目为　　　　　　　　　　　　　　 (　　 )

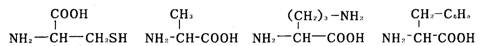
　 　　　　半胱氨酸 　　　　　丙氨酸　 　　　　　赖氨酸　 　　　　苯丙氨酸

　 　　 A．1个　　 　　　　　　 B．2个　　 　　　　　　 C．3个　　　　　　　　　　 D．4个

1．常温下进行下列处理，没有显色反应的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　 　　 A．用吡罗红处理RNA　　 　　　　　　　　　　 B．用碘液处理淀粉溶液

　 　　 C．在豆浆中加入双缩脲试剂　　 　　　　　　 D．在葡萄糖溶液中加入斐林试剂

(17)(本小题满分8分)设数列是等比数列，，已知,　　 (1)求数列的首项和公比；(2)求数列的通项公式。

(18)(本小题满分10分)已知数列 {a_n} 的各项均为正数，且满足a₂=5，

a_n+1 = a_n²－2n a_n+2，(n Î N*)． 推测并证明a_n的通项公式．

(19)(本小题满分10分)已知数列{a_n}中，a₁ =1，前 n 项和为S_n，且点(a_n，a_n+1)在直线

x－y+1=0上． 计算+++…+．

(20)(本小题满分12分)某县与沙漠化进行长期的斗争． 全县面积为 p， 2002 年底绿化率达 ，从 2003 年开始，每年绿化原有沙漠面积的 ，但与此同时，原有绿化面积的 　被沙化． 设2002 年底的绿化面积为 a₁，经过 n 年后的绿化面积为 a_n+1 ．

(I) 求2003年底的绿化面积

(II ) 经过多少年后，绿化率达?

(13)　 已知{a_n}为等差数列，a₁ =2， S₁₀=110． 设a_n =log_0．5 b_n ( n Î N*)，则{b_n}的各项和为 　　　　　．

(14)　 微处理器在诞生后的25年之内，非常准确地遵循“摩尔定律”：半导体芯片每18个月集成度翻番，价格减半． 半导体芯片价格降低，必然导致电脑价格降低． 若每4年电脑的价格降低三分之一，则现价为8100元的电脑12年后价格可能降为 　　　　　． 　

(15)　 在等比数列中，a₉ + a₁₀ = a (a ≠ 0)， a₁₉ + a₂₀ = b，则a₉₉ + a₁₀₀等于 　　　　　　．

(16)　 对于n Î N*，若{a_n}是等差数列，则数列{}也是等差数列．类比上述性质，相应地，若{b_n}是正项等比数列，则数列　　　　　　　　　　　　　　 也是等比数列．

(1)　　　 等差数列 －3，1，5，…的第15 项的值是 (A) 40　　　　　　　　　　　　　 (B) 53　　　　　　　　　　　　　 (C) 63　　　　　　　　　　　　　 (D) 76

(2)　　　 等差数列{a_n} 中，a₃ =2，则该数列的前5项的和为 (A)10 　　　　　　　　　　　　　 (B) 16　　　　　　　　　　　　　 (C) 20　　　　　　　　　　　　　 (D)32

(3)　　　 数列 1， ， ， … ， 的各项和为

(A) 　　　　　　　　　 (B) 　　　　　(C) 　　　　　　　 (D)

(4)　　　 已知数列{a_n}满足a₁ =0，a_n+1 = a_n+2n，那么a₂₀₀₅的值是 (A)2003×2004 　　　　　　 (B)2004×2005 　　　　　　 (C) 2005²　　　　　　　　　　　 (D) 2005×2006

(5)　　　 已知数列 {a_n}(n Î N)中，a₁ = 1，a_n+1 = ，则a_n 为　　　　　　 (A) 2n－1　　　　　　　　　　 (B) 2n + 1　　　　　　　　　　 (C) 　　　　　　　　　 (D)

(6)　　　 在等比数列 {a_n} 中， a₇ a₁₁ =6， a₄ +a₁₄ =5， 则=

(A)　　　　　　　　　　　　　 (B) 　　　　　　　　　　　　　 (C) 或 　　　　　　　　 (D) －或－

(7)　　　 = 　

(A)0　　　　　　　 (B)　　　　　　　　　　　　　　　　 (C)1　　　　　　　 (D) 不存在

(8)　　　 小丁储备2008年赴京观看奥运会的费用，他从2001年起到2007年，每年元旦到银行存入a元一年定期储蓄，若年利率r保持不变，且每年存款到期自动转存新的一年定期． 到2008年元旦将所有的存款和利息悉数取出，可提取

(A) a(1+r)⁸元　 (B) [(1+r)⁷－(1+r)]元　 (C) [(1+r)⁸－1]元　 　 (D) [(1+r)⁸－(1+r)]元

(9)　　　 已知{a_n}是等差数列，{b_n}是正项等比数列，其公比q≠1，若a₁ = b₁，a₁₁ = b₁₁，则 (A) a₆<b₆ (B) a₆ >b₆　　　　　　　　　　 (C) a₆≤ b₆　　　　　　　　　　　　 (D) a₆≥b₆

(10)　 等差数列{a_n}的前n项和为S_n，若a₁ >0，S₄ =S₈，则当S_n取得最大值时，n的值为

(A) 5　　　　　　　　　　　　　　　　　 (B)6 　　　　　　　　　　　　　　 (C) 7　　　　　　　　　　　　　　 (D) 8

(11)　 数列的前n项和为，那么该数列前2n项中所有奇数位置的项的和为　

(A)　　 (B)　　　 (C)　　　　 (D)

(12)　 等差数列的前n项的和分别为，若，则=　

　(A)1　　　　　　 (B)　　　　　　 (C)　　　　　　　　 (D)

　　　　 求函数的极值和单调区间．

(18)(本小题满分10分)

设函数是定义在上的奇函数，当时，

(Ⅰ)当；

(Ⅱ)若在上为增函数，求的取值范围.

(19)(本小题满分10分)

　　　 设函数，点P(x₀，y₀)0＜x₀＜1在曲线上，求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x₀表达)．

(20)(本小题满分12分)

　　　　　　　 某厂生产某种电子元件，如果生产出一件正品，可获利200元，如果生产出一件次品则损失100元.已知该厂制造电子元件过程中，次品率p与日产量x的函数关系是：．

(I)将该厂的日盈利额T(元)表示为日产量x(件)的函数；

　　　 (II)为获得最大盈利，该厂的日产量应为多少件？

(14)函数y=x－2sinx在(0， 2)内的单调增区间为　　　　　　　　　　　　 ．

(15)曲线y=上的点到直线2x－y+3=0的最短距离为　　　　　　　　　　　 ．

(16)向高为8m，底面边长为8m的倒置正四棱锥形的容器内注水，其速度为每分钟，则　 　 当水深为5m时，水面上升的速度为　　　　　　 ．

(1)已知的值是

　　 (A)　　　　　　 (B)2　　　　　　　 (C)　　　　　 (D)－2

(2)

　　 (A)0　　　　　　　 (B)　　　　　 (C)　　　　　 (D)

(3)已知曲线，则过点(1，2)的切线的斜率是

　　 (A)2　　　　　　　 (B)4　　　　　　　 (C)6　　　　　　 (D)8

(4)函数的导数是

　　 (A)　　　　　 (B)　　　　 (C)　　　 (D)

(5)若函数 为R上的连续函数，则a 的值为

　　 (A)2　　　　　　　 (B)1　　　　　　　 (C)0　　　　　　 (D)－1

(6)下列给出的四个命题中，正确的命题是

①若函数

②若函数

③瞬时速度是动点位移函数S(t)对时间t的导数

④曲线在点(0，0)处没有切线

　　 (A)①②　　　　　　 (B)②③　　　　　 (C)①②③　　　　 (D)②③④

(7)函数的导数是

　　 (A)　　　　　　　　 (B)

　　　 (C)　　　　　　　 (D)

(8)为增函数的区间是

　　 (A)　　 　　　　　　　(B)

　　　 (C)　　　　　　　　　 (D)

(9)函数的最大值为

　　　 (A)　　　　　　　 (B)e　　　　　　 (C)　　　　　　 (D)10

(10)半径为r的圆形铁板，受热膨胀，半径r为时间t的函数，其导数(半径膨胀率)为那么其面积的膨胀率

　　　 (A)　　　　　　　 (B)　　　　　 (C)　　　　　 (D)

(11)若f(x)是在(－L，L)内的可导的偶函数，且不恒为0，则

(A)必定是(－L，L)内的偶函数　　　　

(B)必定是(－L，L)内的奇函数

(C)必定是(－L，L)内的非奇非偶函数　

(D)可能是(－L，L)内的奇函数，可能是偶函

(12)已知的值是

　　　 (A)　　　　　　 (B)0　　　　　　　 (C)8　　　　　　　 (D)不存在

(17)(本小题満分12分)

设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作.若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元．求一周内期望利润是多少？

(18)(本小题满分12分)

正四棱柱ABCD－A₁B₁C₁D₁的底面边长是，侧棱长是3，点E、F分别在BB₁、DD₁上，且AE⊥A₁B，AF⊥A₁D．

(Ⅰ)求证：A₁C⊥面AEF；

(Ⅱ)求截面AEF与底面ABCD所成的二面角的大小；

(Ⅲ)求点B到面AEF的距离．

(19)(本小题満分12分)

若数列{}的通项，设数列{}的通项，又记是数列{}

的前n项的积．

(Ⅰ)求，，的值；

　　　 　(Ⅱ)试比较与的大小，并证明你的结论．

(20)(本小题満分12分)

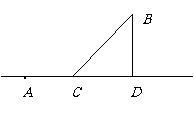如图，有甲乙两个村庄，甲村位于一直线河岸的岸边A处，乙村与甲村在河的同侧，乙村位于离河岸40km的B处，乙村到河岸的垂足D与A相距50km，两村要在此岸边合建一个自来水厂C，从自来水厂到甲村和乙村的水管费用分别为每千米元和元. 现要进行工程费用测算.

(Ⅰ)求出水管总费用关于水厂C到D的距离的函数关系式；

(Ⅱ)问自来水厂C建在何处，才能使水管总费用最省？

(21)(本小题満分12分)

在以O为原点的直角坐标系中，点A(3，－1)为的直角顶点. 已知|AB|=2|OA|，且点B的纵坐标大于零.

　　 (Ⅰ)求向量的坐标；

　　 (Ⅱ)是否存在实数a，使二次函数的图像上总有关于直线OB对称的两个不同的点？若不存在，说明理由；若存在，求a的取值范围.

(22)(本小题満分14分)

已知上是增函数，在[0，2]上是减函数，且方程有三个根，它们分别为．

　　　 (Ⅰ)求c的值；

　　　 (Ⅱ)求证；

　　　 (Ⅲ)求的取值范围．

(13)平面内一动点P到直线2x+3y＝0和到点M(1，1)的距离相等，则P点的轨迹为______________ (写出轨迹名称)．

(14)函数y＝(≤x≤0)的反函数为_______________．

(15)若甲以10发8中，乙以10发6中，丙以10发7中的命中率打靶，三人各射击一次，则三人中只有一人命中的概率是___________．

(16)一个三位数abc称为“凹数”，如果该三位数同时满足a＞b且b＜c，那么所有不同的三位“凹数”的个数是_____________________．