
10.
已知 、
、 ,从点
,从点 射出的光线经直线
射出的光线经直线
反向后再 射到直线 上,最后经直线
上,最后经直线 反射后又回到
反射后又回到
 点,则光线所经过的路程是 ( )
点,则光线所经过的路程是 ( )
A. B.
B. C.
C. D.
D.
9. 数列 满足
满足 若
若 , 则数列的第2009项为 ( )
, 则数列的第2009项为 ( )
A. B.
B. C.
C. D.
D.
8. 已知y = f (x)是定义在(–2,2)上的偶函数,且f (x)在[0,2)上是增函数,若f (m–2) – f(m + 1)<0,则实数m的取值范围是( )
A.(0,1) B.( ,1) C.(0,
,1) C.(0, ) D.(
) D.( ,2)
,2)
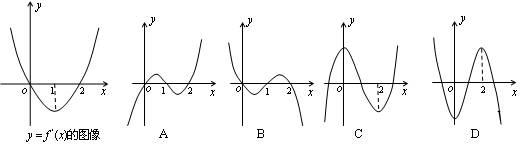
6.设 是函数
是函数 的导函数,
的导函数, 的图象如图所示,则
的图象如图所示,则 的图象最有可能的是( )
的图象最有可能的是( )
7. 函数 的零点个数是( )
的零点个数是( )
A.6 B.8 C.4 D.2
5. 关于平面向量的命题① ·
· =
= ·
· 且
且 ≠
≠ 时,必有
时,必有  =
=  ; ②如
; ②如 //
// 时,必存在唯一实数
时,必存在唯一实数 使
使 =
=
 ;③
;③ ,
, ,
, 互不共线时,
互不共线时,

 必与
必与 不共线;④
不共线;④ 与
与 共线且
共线且 与
与 也共线时,则
也共线时,则 与
与 必共线。其中正确命题个数有 (
)
必共线。其中正确命题个数有 (
)
A.0个 B.1个 C.2个 D.3个
4. 函数 的图象经过适当变换可以得到
的图象经过适当变换可以得到 的图象,则这种变换可以是( )
的图象,则这种变换可以是( )
A. 沿x轴向右平移 个单位 B. 沿x轴向左平移
个单位 B. 沿x轴向左平移 个单位
个单位
C. 沿x轴向左平移 个单位 D.沿x轴向右平移
个单位 D.沿x轴向右平移 个单位
个单位
3. 等比数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于( )
等于( )
A. B.5
C.
B.5
C. D.33
D.33
2. 已知 ,
, ,则
,则 是
是 的( )
的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分又不必要条件
1. 若 ,则集合
,则集合 的元素个数为( )
的元素个数为( )
A.2 B.3 C.4 D.5
22.(本小题满分14分)若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线
 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求 的极值;
的极值;
(2) 函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
福建省泉州七中2010届高三上学期第三次月考
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com