4.两个非零向量的模相等是两个向量相等的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

3.要得到函数y=cos()的图象，只需将函数y=sin的图象

A.向左平移个单位　　　　　　　　　　　　　　　　　　　 B.向右平移个单位

C.向左平移个单位　　　　　　　　　　　　　　　　　　　 D.向右平移个单位

2.已知等差数列前n项和为S_n，若S₁₂＞0，S₁₃＜0，则此数列中绝对值最小的项为

A.第5项　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.第6项

C.第7项　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.第8项

1.已知全集为R，集合A={x∈R|f(x)=0},B={x∈R|g(x)=0}，则不等式f(x)g(x)≠0的解集为

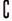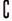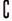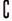A.(_RA)∩(_RB)　　　　　　　　　　　　　　　 　　　　　　　 B.(_RA)∪(_RB)

C.(B∩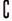_RA)∪(A∩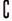_RB)　　　　　　　　　　　　　　　　　 D.(B∪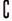_RA)∪(A∪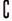_RB)

22．(本小题满分12分)

数列{}中，a₁＝2，a₂＝8，且－4+4＝0．

(1)求{}的通项;

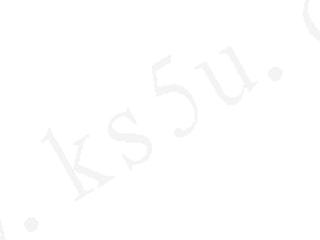(2)若m为正整数，当2≤n≤m时，求证(m－n+1) ≤.

21．(本小题满分12分)

已知椭圆C₁：(a>b>0)的离心率为，直线l：y＝x+2与以原点为圆心，以椭圆的短半轴长为半径的圆相切，抛物线C₂：x²＝2py(p>0)的焦点与椭圆C₁的其中一个焦点重合．

(1)求抛物线C₂的方程；

(2)过抛物线C₂上一点P的直线m交抛物线于另一点Q，若直线m不过原点且与x轴交于点S，与y轴交于点T，试求+的取值范围．

20．(本小题满分12分)

已知f(x)＝(x²+ax+a)(a≤2)．

(1)当a＝1时，求f(x)的单调区间；

(2)是否存在实数a，使f(x)的极大值为3?若存在，求出a值；若不存在，请说明理由．

19．(本小题满分12分)

某大学选拔参加某项国际大赛的学生，由每位参加选拔的同学同时进行四种不同的物理实验，至少有三种实验成功即可获得通过，假设每位同学做每种实验成功的概率均为，且每种实验成功与否相互独立．

(1)求甲同学获得通过的概率；

(2)若三人同时参加选拔，求获得通过的人数ξ的分布列及期望．

18．(本小题满分12分)

如图，四棱锥P－ABCD中，zxxk底面ABCD为矩形，侧

面△PDC为等边三角形，且平面PDC⊥平面ABCD，

AB＝2,BC＝2，M为BC的中点．

(1)证明：AM⊥PM；

(2)求二面角P－AM－D的大小．

17．(本小题满分10分)

已知△ABC的面积S满足≤S≤3，且·＝6．

(1)求角B的取值范围；

(2)若θ＝π－B，求f(θ)＝2cosθsinθ+2+1的最小值．