

[分析] 本题主要考查二项式定理的应用,以及基本的计算技能.
直接利用二项展开式的通项公式,便可求得 的系数,如解法1.由于二项式中的两个项都含有x,因此将其适当变形,有利于简化计算,如解法2.试题的这种设计,体现了对计算灵活性和准确性的要求.
的系数,如解法1.由于二项式中的两个项都含有x,因此将其适当变形,有利于简化计算,如解法2.试题的这种设计,体现了对计算灵活性和准确性的要求.
解法1 设所求系数为a,则由二项展开式的通项公式,知存在非负整数r,使



解得r=3,所求系数为

解法2 因为




14.某公司生产三种型号的轿车,产量分别为1 200辆,6 000辆和2 000辆.为检验该公司的产品质量,现用分层抽样方法抽取46辆进行检验,这三种型号的轿车依次应抽取____________,_______________,____________辆.
[分析] 本题主要考查分层抽样方法在产品质量检验中的应用,以及简单的数值计算技能.
设三种型号的轿车抽取数依次为x,y,z辆.根据分层抽样方法的原理,知

这个方程组可用不同方法求解.
解法1 由比例式知存在常数k满足



解法2 由此例式得
60x=12y,
20x=12z,




[答案] 6,30,10
12.一个四面体的所有棱长都为 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
A.3π B.4π  D.6π
D.6π
[分析] 本题主要考查正多面体和球的基本知识,以及空间想象能力和几何计算能力.
本题给出棱长为 的正四面体,要求推断外接球的表面积.为此,必须先求该球的半径,宜作图进行推算或估算.为了图像清晰,可只作正四面体进行讨论,不画出球的图线.如附图,四面体ABCD各棱长都为
的正四面体,要求推断外接球的表面积.为此,必须先求该球的半径,宜作图进行推算或估算.为了图像清晰,可只作正四面体进行讨论,不画出球的图线.如附图,四面体ABCD各棱长都为 .
.
解法1 如图,点O为球心,OA、OB、OC、OD都是球的半径,因为ABCD是正四面体,所以这四条半径的两两夹角彼此相等,设其大小为θ.
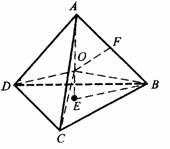
由空间中的一点O,引四条射线,两两的夹角都等于θ,则有





据此,可排除选项B、C和D,应取A作答.
解法2 如图,过A作AE⊥面BCD,E是垂足.连结EB,则EB是正△BCD外接圆的半径.应用正弦定理,由正三角形的边长为 得
得

因为 AE⊥EB

过AB的中点F,在平面AEB中,作AB的垂线交AE于O,则O是四面体ABCD外接球的球心,球的半径为

所以,所求的球之表面积为

上述估计和精算的方法,计算量仍嫌偏大.若充分发挥空间想像力,可获快速判断.
解法3 联想棱长为1的正方体 则四面体
则四面体 的棱长都为
的棱长都为 它的外接球也是正方体的外接球,其半径为正方体对角线长
它的外接球也是正方体的外接球,其半径为正方体对角线长 的一半,即有
的一半,即有 故所求球面积为S=3π.
故所求球面积为S=3π.
[答案] A
10.已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点 沿与AB夹角为θ的方向射到BC上的点
沿与AB夹角为θ的方向射到BC上的点 后,依次反射到CD、DA和AB上的点
后,依次反射到CD、DA和AB上的点 (入射角等于反射角).设
(入射角等于反射角).设 的坐标为
的坐标为 则tanθ的取值范围是
则tanθ的取值范围是




[分析] 本题以运动质点碰壁反射问题为背景,主要考查直线、轴对称和函数等基础知识及其应用,以及分析解决问题的能力.
依题意可知点 的横坐标
的横坐标 是tanθ的函数,试题要求由
是tanθ的函数,试题要求由 的取值范围确定tanθ的取值范围,也即由函数的值域求定义域.为此,宜从建立函数关系式入手,如解法2.不过,作为选择题,本题可以用特殊值排除法快速求解,如解法1.
的取值范围确定tanθ的取值范围,也即由函数的值域求定义域.为此,宜从建立函数关系式入手,如解法2.不过,作为选择题,本题可以用特殊值排除法快速求解,如解法1.
解法1 取特殊的θ角,当 时,根据反射原理,得点
时,根据反射原理,得点 依次是BC,CD,DA和AB的中点,即有
依次是BC,CD,DA和AB的中点,即有 不属于所求的tanθ的取值范围.从而,可排除选项A、B和D,应取C作答.
不属于所求的tanθ的取值范围.从而,可排除选项A、B和D,应取C作答.
解法2 依题设可作图如下.记各点的坐标如下:

根据反射原理得:






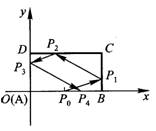
[答案] C

A.3 
 D.6
D.6
[分析] 本题主要考查组合数的性质、数列极限的计算等基本知识,以及基本的计算技能.
本题要求考生计算两个和式之比的极限.由于和式的项数随n的增加而无限增加,因而不能简单应用极限四则运算法则求极限,必须将和式化简成有限的形式.
原式中,分子、分母的和式是组合数求和,应充分借助组合数性质,将其化简.例如,应用公式

可顺利化简原式.
此外,也可采用数列求和的方法求解.





[答案] B
9.已知双曲线中心在原点且一个焦点为 ,直线y=x-1与其相交于M、N两点,MN中点的横坐标为
,直线y=x-1与其相交于M、N两点,MN中点的横坐标为 则此双曲线的方程是
则此双曲线的方程是




[分析] 本题主要考查双曲线的基本知识,以及推理和计算技能.
本题要求确定双曲线的方程,而双曲线的已知条件比较复杂,涉及到与已知直线相交的背景.在这种情况下,宜用待定系数法求解.
因为双曲线的中心在原点,点 又是双曲线的一个焦点.故双曲线的方程可写为
又是双曲线的一个焦点.故双曲线的方程可写为

a>0为待定系数,可用不同方法求得.
解法1 将y=x-1代人方程①,整理得

由直线y=x-1与双曲线相交于M、N两点,故此二次方程有不等的两个实根 分别为点M、N的横坐标.从而MN中点的横坐标为
分别为点M、N的横坐标.从而MN中点的横坐标为



解法2 依题设,可记

其中t为某个常数,且t≠0.
由M、N在双曲线上,得

将两式相减,整理得



上述解法计算量偏大,为了快速解答,可采用定性与定量相结合的方法求解.
解法3 由双曲线与直线y=x-1有两个交点M和N,且焦点在x轴上,可知双曲线渐近线的斜率绝对值应大于1,由此排除B、C;其次,由MN的中点的横坐标为 可估计双曲线的张口应比较大,D的可能性比较大.为此,作定量检验,将直线方程代人A所示的双曲线得
可估计双曲线的张口应比较大,D的可能性比较大.为此,作定量检验,将直线方程代人A所示的双曲线得


[答案] D
8.已知方程 的四个根组成一个首项为
的四个根组成一个首项为 的等差数列,则|m-n|=
的等差数列,则|m-n|=
A.1 


[分析] 本题主要考查二次方程根与系数的关系,等差数列等基本知识,以及数学思维和分析处理问题的能力.
注意到题设4次方程的两个2次因式中,只有常数项不同,可知等差数列的4个项中首尾两项应为其中一个因式的两根,而中间两项为另一因式的两根.所以,在此基础上,可用不同的引入方式,采取适当的计算程序,求得|m-n|的值.
解法1 因为抛物线 有公共的对称轴x=1,又它们与x轴的4个交点的横坐标(即题设方程的4个根)成等差数列,所以可设为
有公共的对称轴x=1,又它们与x轴的4个交点的横坐标(即题设方程的4个根)成等差数列,所以可设为






的一个根,则方程的另一个根为








解法3 依题意可设原方程的4个根为

则对任意实数x,有


比较系数,得

(注:m、n的位置也可对调,不影响结果).


解法4 从解原方程入手.由

求得原方程的根为:

由题设,这4个根组成首项为 的等差数列,所以,必有1-m>0,1-n>0,且
的等差数列,所以,必有1-m>0,1-n>0,且







[答案] C
7.设 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为 ,则点P到曲线y=f(x)对称轴距离的取值范围为
,则点P到曲线y=f(x)对称轴距离的取值范围为




[分析] 本题主要考查导数的几何意义,多项式函数求导数的方法,点到直线的距离,二次函数的性质等基本知识,以及推理和计算技能.
解答本题,宜先求出 的取值范围,进而根据曲线y=f(x)对称轴的方程,便可求得点P到对称轴距离的取值范围,如解法1.此外,也可用特殊值排除法求解.
的取值范围,进而根据曲线y=f(x)对称轴的方程,便可求得点P到对称轴距离的取值范围,如解法1.此外,也可用特殊值排除法求解.
解法1 依题设知点P的横坐标 必须且只须满足
必须且只须满足



因为抛物线y=f(x)的对称轴为直线 :
:

所以点P到直线 的距离为
的距离为




解法2 取特殊值a=1,b=-2,c=0.可知曲线y=f(x) 的对称轴为直线l:x=1.曲线在点P处切线的斜率为
的对称轴为直线l:x=1.曲线在点P处切线的斜率为

由 及tanx的单调性,依题设知k的取值范围为[0,1],所以
及tanx的单调性,依题设知k的取值范围为[0,1],所以

 得点P到对称轴
得点P到对称轴 距离的取值范围为
距离的取值范围为 据此,可排除选项A,C,D,得答案B.
据此,可排除选项A,C,D,得答案B.
[答案] B
6.棱长为a的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为




[分析] 本题主要考查棱柱、棱锥等多面体的基本知识和体积计算,以及基本的空间想象能力.
题设的八面体(记为ABCDEF)如图所示.图中将原正方体略去,以使图线清晰.该八面体的三条轴线AC、BD、EF两两互相垂直,且AC=BD=EF=a,

把这个八面体看作共底(BFDE)的两个四棱锥的组合体,应用棱锥体积计算公式,得所求的八面体的体积为

对于空间想像力比较好的考生,不作图便可由心算得出答案.心算的方法比较多,例如,与上法共通地把八面体看作共底的两个四棱锥,底面积是正方体的一个面的面积之半,锥高是正方体棱长之半,即可得体积为 又如,由对称性,将正方体切成相等的八个小正方体,这时题没的八面体也被切成八个相等的三棱锥,每个三棱锥的体积等于小正方体的体积的
又如,由对称性,将正方体切成相等的八个小正方体,这时题没的八面体也被切成八个相等的三棱锥,每个三棱锥的体积等于小正方体的体积的 所以八面体的体积是正方体体积的
所以八面体的体积是正方体体积的 即
即
[答案] C





[分析] 本题主要考查复数的四则运算,以及简单的数值计算技能.
解答本题必须正确用好复数的四则运算法则,既可用复数的代数形式进行演算,也可用三角形式进行演算.



[答案]B





[分析] 本题主要考查三角函数的基础知识和基本三角函数公式的简单应用,以及基本的计算技能.
作为常规解法,可先由已知条件求sin x,推得tan x的值,再应用倍角正切公式求得答案,如解法1;作为灵活解法,可用估值快速求解,如解法2.




(注:也可用下式得解:

而不需求tanx.)



[答案] D

A.(-1,1) B.(-1,+∞)
C.(-∞,-2)∪(0,+∞) D.(-∞,-1)∪(1,+∞)
[分析] 本题主要考查分段函数的概念、指数函数与幂函数的性质、不等式组的求解等基础知识,以及简单的推理计算能力.
根据函数f(x)的分段表达式,画个草图可快速判断,如解法4;也可将不等式 化为等价的不等式组求解,如解法1;也可用特殊值排除法求解,如解法2;还可以利用单调性,结合解方程求解,如解法3.
化为等价的不等式组求解,如解法1;也可用特殊值排除法求解,如解法2;还可以利用单调性,结合解方程求解,如解法3.


解不等式组①得 解不等式组②得
解不等式组②得 综合得
综合得 的取值范围为(-∞,-1)∪(1,+∞).
的取值范围为(-∞,-1)∪(1,+∞).
解法2 由 排除A和B;由f(0.04)=0.2<1,排除C,得答案D.
排除A和B;由f(0.04)=0.2<1,排除C,得答案D.

解得x=-1;由

解得x=1.
因为f(x)在(-∞,0]上是减函数,在(0,+∞)上是增函数,所以得 的取值范围为(-∞,1)∪(1,+∞).
的取值范围为(-∞,1)∪(1,+∞).
[答案] D
4.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足

则P的轨迹一定通过△ABC的
A.外心 B.内心 C.重心 D.垂心
[分析] 本题主要考查平面向量的线性运算等基本知识和计算技能.
解法1 为书写方便与直观起见,宜作图表示(如下图).图中,有

则动点P满足



因此,点P的轨迹一定通过△ABC的内心.得答案为B.
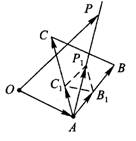
解法2 当λ>0时,





因为A,B,C不共线,
所以AP平分∠BAC,
得点P的轨迹一定通过△ABC的内心.
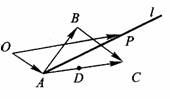
解法3 考虑特殊情形,取△ABC为等腰直角三角形,即: 如图.
如图.
这时,△ABC的外心为AC的中点D,垂心为点B.而由题设知点P的轨迹是由点A出发,方向为 的射线
的射线 ,不经过点D,也不经过点B,故排除A、D两个选项.其次,由于
,不经过点D,也不经过点B,故排除A、D两个选项.其次,由于 所以射线
所以射线 不平分BC,即不通过△ABC的重心,排除选项C.从而得选项B为答案.
不平分BC,即不通过△ABC的重心,排除选项C.从而得选项B为答案.
[答案] B





[分析] 本题主要考查对数函数、指数函数的性质和求反函数的方法,以及基本的计算技能.
根据反函数的概念,求给定函数的反函数,可用解方程的方法,如解法1;作为选择题,还可用特殊值排除法求解,如解法2.
解法1 解方程不等式组




得y>O,因此,所求的反函数为

解法2 因为点(2,ln3)在原函数的图像上,所以点(1n3,2)应在反函数的图像上.因此,由In3>0,可排除选项C、D;由
可排除A,应取B作答.
[答案] B
22.(本小题满分14分)
设f(x)的定义域为x∈R且x≠ ,k∈Z,且
,k∈Z,且 ,如果f(x)为奇函数,当0<x<
,如果f(x)为奇函数,当0<x< 时,f(x)=3x.
时,f(x)=3x.
(1)求
(2)当 <x<2k+1(k∈Z)时,求f(x);
<x<2k+1(k∈Z)时,求f(x);
(3)是否存在这样的正整数k,使得当 <x<2k+1(k∈Z)时,log3f(x)>x2-kx-2k有解?
<x<2k+1(k∈Z)时,log3f(x)>x2-kx-2k有解?
21.(本小题满分12分)
设曲线C:y=x2(x>0)上的点P0(x0,y0),过P0作曲线C的切线与x轴交于Q1,过Q1作平行于y轴的直线与曲线C交于P1(x1,y1),然后再过P1作曲线C的切线交x轴于Q2,过Q2作平行于y轴的直线与曲线C交于P2(x2,y2),依次类推,作出以下各点:P0,Q1,P1,Q2,P2,Q3,…,Pn,Qn+1,…,已知x0=2,设Pn(xn,yn)(n∈N*).
(1)求出过点P0的切线方程;
(2)设xn=f(n),求f(n)的表达式;
(3)设Sn=x0+x1+…+xn,求 Sn.
Sn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com