3.　 在中. 若 ，则 　　　　　　　　　　　　(C)

　　 A. 　　　　　　　　 　　B.　 　　　　　　　C.　 　　　　　　D.　

　答：

2. 　的近似值(精确到小数后第三位)为　　　　　　　　　　　　　 (A)

　 　A.　 726.089　　　 　 B.　 724.089　　　　 　　　 C.　 726.098　　　 　 D.　 726.908

　 　答：

1.已知集合P={(x，y)||x|+|y|=1}，Q={(x，y)|x²+y²≤1}，则　　　　　　 (A)

A.PQ　　　　　 B.P=Q　　　　　 C.PQ　　　　　 D.P∩Q=Q

　 　答： 集合P表示正方形，集合Q表示圆面.

21．已知常数a>0，向量c=(0，a)，i=(1，0)．经过原点O以c+λi为方向向量的直线与经过定点A(0，a)以i－2λc方向向量的直线相交于点P，其中λ∈R．试问：是否存在两个定点E、F，使得|PE|+|PF|为定值．若存在，求出E、F的坐标；若不存在，说明理由．

[命题意图]　 本题主要考查平面向量的概念和向量的线性运算，根据已知条件求动点的轨迹方程，并讨论轨迹曲线的性质，着重考查直线、圆和椭圆等平面解析几何的基础知识，以及综合应用所学知识分析和解决问题的能力．

试题用向量的形式给出两条相交直线的条件，围绕交点P提出个一个探索性的问题：讨论是否存在两个定点，使得点P到这两个定点距离之和为一定值．在这里，点P因实数λ的变化而动．考生在审题时，必须自觉理解到问题的这个特点，具备“运动变化”和“动中求静”的辩证法的思想和观点，只有这样才能有效破题，获得问题的解答．可见试题重在考查思维和分析的能力．同时，该题的设计，围绕平面解析几何的主体知识，将传统的坐标法与向量法有机结合起来，旨在考查综合应用能力．

[解题思路]　 有关存在性问题的讨论，许多时候可用构造法，这是一种基本的，而且也是比较原始的方法．就本题而言，即假设符合要求的定点存在，依题意列写出定点坐标所满足的方程，进而探求方程的解是否存在．依此思路，由于未知量比较多，方程的列写也难以简明，因而推演起来工作量大，而且繁杂．显然采用构造法绝非上策，宜另谋出路．

从试题的实际出发，联想广泛可用的知识，才能获得有效的求解思路和方法．题设的点P是两条动直线的交点，随着λ取遍实数集R中所有的值，点P的集合是一条轨迹曲线．另一方面，到两个定点距离之和为一定值的点之集合可能有两种情况：其一，当定值大于两个定点的距离时，该点集是椭圆曲线；其二，当定值等于两个定点的距离时，该点集是连结两点的线段．由于平面上到两个定点距离之和不可能小于两定点的距离，所以也就不可能出现第三种情况．由这样的思考，可得解题思路如下：

从求点P的轨迹方程入手，进而讨论轨迹曲线的性质，便可获得本题的答案．

由题设，可作图观察．图中，向量直线分别过点O和A，其方向向量分别为c+λi和i－2λc，点P是的交点．为了求点P的轨迹方程，可采用不同的方法．在这里，有一点值得注意的是：试题本身并没有要求考生求点P的轨迹方程，我们是借助轨迹的思想，只须求出点P的坐标所应满足的方程，进而展开讨论，而无须检验满足方程的每一个解为坐标的点都是符合题意的点P，也即无须要求所得方程的纯粹性，与严格意义上的求轨迹方程有所不同．

解法1　 因为 c+λi=(0,a)+ λ(1,0)=(λ,a),

　　　　　　 i-2λc=(1,0)-2λ(0,a)=(1,-2λa),

所以　 直线OP与AP的方程分别为

　　　　　　　 λy=ax

　　　　　　　 y-a=-2λax,

式中，a>0,λ∈R．

整理得

因为a>0,所以得：

(i)当时，方程①是圆方程，故不存在合乎题意的定点E和F；

(ii)当时，方程①表示椭圆，故焦点为合乎题意的两个定点；

(iii)时，方程①也表示椭圆，故焦点为合乎题意的两个定点．

解法2 　依题设，有实数m和n满足

所以点P(x,y)的坐标为

整理得点P的坐标满足方程

以下的讨论同解法1．此处从略．

[命题意图]　 本小题主要考查数列、等比数列的基础知识和数学归纳法，同时考查抽象推理等理性思维能力．

数学高考中较难的数列解答题，一般都是给出一个递推关系，通过它或者转化为等差、等比数列，或者通过由特殊到一般的猜想、归纳，或者通过顺次迭代，以求出其通项．而试题的难度则由给出的递推关系与初始值来调整．2002年的数列解答题给出相邻四项的数量关系，较为新颖，2003年定位于回归到考生较为熟悉的相邻两项的数量关系，基本递推关系为“”．理科试题改变以往给出初始值的做法，给出常数证明数列的一个通项公式。这种提问方式反映出新的考查角度，不让考生死套题型，有利于考查独立思考能力和理性思维能力，对文科考生则降低抽象思维的要求，递推关系简化为基本形式“”，并给出初始值a=1，使试题难度较为切合文科考生的实际．

[解题思路]　 常规方法是通过递推关系的变形转化为等比数列，但过程较繁，用数学归纳法或迭代方法较顺畅．

(Ⅰ)证法1　 (i)当n=1时，由已知等式成立；

(ii)假设当n=k(k≥)时等式成立，即

也就是说，当n=k+1时，等式也成立．

根据(i)和(ii)，可知等式对任何正整数n成立．

证法4顺次迭代

(i)当n=2k-1,k=1,2,…时，①式即为

②式对k=1,2,…都成立，有

(ii)当n=2k,k=1,2,…时，①式即为

③式对k=1,2,…都成立，有

[以下同解法1]

解法3　

下面证明当

(i)当n=2k-1,k=1,2,…时，

(ii)n=2k,k=1,2…时，

20．A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是B队队员是按以往多次比赛的统计，对阵队员之间胜负概率如下：

现按表中对阵方式出场，每场胜队得1分，负队得0分．设A队、B队最后所得总分分别为ξ、η．

对阵队员	A队队员胜的概率	A队队员负的概率

(Ⅰ)求ξ，η的概率分布；

(Ⅱ)求Eξ，Eη．

[命题意图]　 本题主要考查离散型随机变量分布列和数学期望等概念与计算，以及运用概率知识认识和讨论实际问题的能力．

该题的取材贴近考生日常生活，以广大考生都熟悉的乒乓球比赛为素材，用列表的方式，给出对阵队员间胜负的概率，并规定每场胜负的得分规则．这样的条件下，赛后球队所得总分是离散型随机变量．本题要求考生计算该随机变量的分布列和数学期望．

这样设计试题，应用性强，也能贴近考生实际，符合《考试说明》的要求．

[解题思路]　 为了求随机变量ξ和η的概率分布，必须先确定它们是离散型还是连续型．依题意，它们都是离散型随机变量，且满足ξ+η=3．所以只须求出ξ(或η)的概率分布，便可立即写出η(或ξ)的概率分布．

为了求ξ的概率分布，首先应弄清ξ可能取哪些值?这些值表示怎样的随机事件?进而应用随机事件概率计算公式(如乘法公式、加法公式等)，求出ξ取每一个可能值的概率，使得到所要求的概率分布列．

至于第(Ⅱ)问，可直接应用离散型随机变量数学期望的计算公式求解．

因为ξ是A队赛后所得的总分，根据题意，ξ只可能取0，1，2，3等4个值，其表示的随机事件分别为：

ξ=表示A队3场比赛都输球，全负；

ξ=1表示A队3场比赛中1胜2负；

ξ=2表示A队3场比赛中2胜1负；

ξ=3表示A队3场比赛全胜．

所以由给出的胜负概率表，应用互斥事件概率的加法公式、独立事件的概率加法公式等相关公式，便可求得ξ的分布列．

(Ⅰ)解　 ξ、η的可能取值都为3，2，1，0．ξ的分布为：

依题意，ξ+η=3，故η的分布为：

19．设a>0，求函数．

[命题意图]　 本题主要考查函数的求导，导数在研究函数性质中的应用和不等式的求解等基本知识，以及运算能力．

本题给出的函数比较简单，为幂函数与对数函数ln(x+a)之差，让考生求这个函数的单调区间．直接应用单调函数的定义，难以进行有效的讨论，宜借助求导的方法求解．以此可以考查函数求导的技能，以及讨论导数正负性的方法．

所设的函数含有参数a，讨论函数单调区间时，应顾及a值的影响．这样，也就考查了分类讨论的数学方法，强化了试题对能力的考查功能．

[解题思路]　 可从求函数的导数入手，再讨论导数的正负性变化区间，便可确定函数的单调区间．由于所得导数含有x的根式和分式，在讨论导数正负性时，将遇到解含根式和分式的方程或不等式，须正确运用同解变换的思想方法和技能．

(i)当a>1时，方程①无解，即f′(x)＝0无解，f′(x)在区间(0，+∞)上正负性不变，故由

知f′(x)>0在区间(0，+∞)上恒成立，所以(0，+∞)是f(x)的单调区间，f(x)在(0，+∞)上是增函数．

(ii)a=1时，方程①有惟一解x=1．

知当0<x<1时，恒有f′(x)>0；由f′

知当x>1时，恒有f′(x)>0．

所以，当a=1时，函数f(x)在区间(0，1)上是增函数，在区间(1，+∞)上也是增函数．又f(x)在x=1连续，所以(0，+∞)是f(x)的单调区间，f(x)在(0，+∞)上是增函数．

(iii)当0<a<1时，方程①有两个根：

这时,由于

可知：当0<x<或

所以，当0<a<1时，都是单调区间，f(x)在这两个区间上都是增函数；也是单调区间，f(x)在这个区间上是减函数．

(i)当a>1时,2a-4>-2,由x>0知

(ii)当a=1时,

当且仅当x=1时取等号．即当0<x<1或x>1时，f′(x)>0，知f(x)在(0，1)或(1，+∞)内都单调递增．又f(x)在x=1处连续，因此，f(x)在(0，+∞)内单调递增．

因此，函数f(x)在区间内单调递增，在区间内也单调递增．

令f′(x)<0，即

因此，函数，f(x)在区间内单调递减．

18．如图，在直三棱柱底面是等腰直角三角形，∠ACB=90°．侧棱的中点，点E在平面ABD上的射影是△ABD的重心G．

(Ⅰ)求与平面ABD所成角的大小(结果用反三角函数值表示)；

[命题意图]　 本小题主要考查线面关系和直三棱柱等基础知识，同时考查空间想象能力和推理运算能力．

新课程的立体几何教材分为(A)、(B)两个版本，即传统的逻辑推理体系和向量运算方法．为了．适应不同地区的选用情况，前几年高考的立体几何试题是命制出(甲)、(乙)两道平行题目由考生选作．今年试验改变这种做法，原课程与新课程统一命制一道通用的试题，基本要求是用传统方法或向量方法，解题难度相当．于是，试题的知识载体定位于直棱柱．理科用直三棱柱，文科用正四棱柱．

理科试题中的图形实际上是半个正方体，它的原型是正方体的一个性质：“若点M是正方体的棱的中点，则正方体的中心O在截面AMC上的射影恰好是△AMC的重心”．试题基本上是采用其逆命题，且只给出半个正方体，把问题提为“正方体的一条对角线与截面所成的角”，隐蔽了上述性质，提高了对考生空间想像力和推理能力的要求，以期更好地考查考生的数学能力．

[解题思路]　 本题(Ⅰ)的基本解法是先求出三棱柱的底面边长，可以在直三棱柱中求解，也可以补形成正四棱柱或直平行六面体求解，思维层次高者可以发现EB=DF避开计算，通过线段比求角的三角函数值．(Ⅱ)问的解法用等积法最为简便．运用向量方法则(Ⅰ)问较易，(Ⅱ)问较难，总体难度相当．

(Ⅰ)解法1　 如图，连结BG，则BG是BE在面ABD的射影，即∠EBG是与平面ABD所成的角．

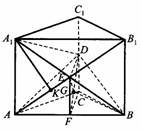
设F为AB中点，连结EF、FC，

因为D、E分别是的中点，又DC⊥平面ABC，

所以CDEF为矩形．

连结DF，G是△ADB的重心，故G∈DF．在直角三角形EFD中，

解法2　 同解法1图．

所以　 AB·DF·EG=AB·EF·DE，其中EF=1．

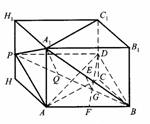
的中点P,连结PD,PA,PB,则ABDP是平行四边形,PB必过△ADB的重心．

解得x=2

解法4　 如解法1图，由解法1知，CDEF是矩形，故DE=CF，而EF=FB，所以Rt△DEF≌△CFB，则DF=EB．

解法5　 连结BG，则BG是BE在面ABD的射影，即与平面ABD所成的角．

如图所示建立坐标系，坐标原点为O．

设CA=2a，则A(2a，0，0)，B(0，2a，0)，D(0，0，1)，,E(a，a，1)，

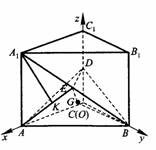
(Ⅱ)解法1　 因为ED⊥AB，ED⊥EF，又EF∩AB=F，

　

因为ED⊥AB，ED上⊥EF，又EF∩AB=F，

解法3　 如(Ⅰ)问解法5中图，A(2，0，0)，E(1,1,1),D(0，0，1)．

17．已知函数f(x)=2sinx(sinx+cosx)．

(Ⅰ)求函数f(x)的最小正周期和最大值；

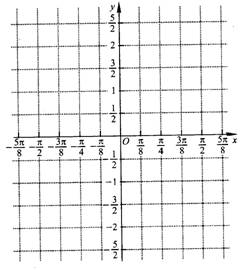
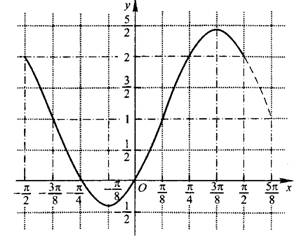
(Ⅱ)在给出的直角坐标系中，画出函数y=f(x在区间上的图象．

[命题意图]　 本小题主要考查三角函数的性质和恒等变形的基础知识，同时考查动手画图的技能．

作为三角函数的解答题，力求较全面地覆盖三角函数的基础知识，因此，试题的设计给出一个三角函数的解析式，通过运用和角与倍角的三角函数公式，变形为单个三角函数的表达式，从而求出它的周期和最值．恒等变形过程强调通性通法，以适应文科考生的实际．在这个基础上要求作出这个函数的图像，强化了作图技能的考查，倡导考生重视实践，学会动手操作．

[解题思路]　 首先把给出的函数解析式变形为单个三角函数的表达式，再按问题的要求答题．

(Ⅱ)解　 由(Ⅰ)知

x
Y	1		1		1

16．下列5个正方体图形中，l是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出⊥面MNP的图形的序号是_______．(写出所有符合要求的图形序号)

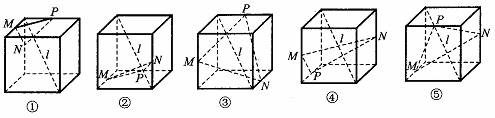
[分析]　 本题以正方体为依托，主要考查直线与平面垂直的判定，比较深刻地考查了空间想象能力．

为了得到本题答案，必须对5个图形逐一进行判别．对于给定的正方体，位置固定，截面MNP变动，与面MNP是否垂直，可从正、反两方面进行判断．在MN、NP、MP三条线中，若有一条不垂直，则可断定与面MNP不垂直；若有两条与都垂直，则可断定⊥面MNP；若有的垂面∥面MNP，也可得⊥面MNP．

解法1　 作正方体如附图，与题设图形对比讨论．在附图中，三个截面都是对角线的垂面．

对比图①，由MP∥BD,，故得⊥面MNP．

对比图②，由MN与面相交，而过交点且与垂直的直线都应在面内，所以MN不垂直于，从而不垂直于面MNP．

对比图③，由MP与面相交，知不垂直于MN，故不垂直于面MNP．

对比图④，由MN∥BD，故⊥面MNP．

对比图⑤，面MNP与面EFGHKR重合，故⊥面MNP．

综合得本题的答案为①④⑤．

解法2　 如果记正方体对角线所在的对角截面为α．各图可讨论如下：

在图①中，MN，NP在平面α上的射影为同一直线，且与垂直，故⊥面MNP．事实上，还可这样考虑：在上底面的射影是MP的垂线，故⊥MP；在左侧面的射影是MN的垂线，故⊥MN，从而⊥面MNP．

在图②中，由MP⊥面α，可证明MN在平面α上的射影不是的垂线，故不垂直于MN．从而不垂直于面MNP．

在图③中，点M在α上的射影是的中点．点P在α上的射影是上底面的内点，知MP在α上的射影不是的垂线，得不垂直于面MNP．

在图④中，平面α垂直平分线段MN，故⊥MN．又在左侧面的射影(即侧面正方形的一条对角线)与MP垂直，从而⊥MP，故⊥面MNP．

在图⑤中，点N在平面α上的射影是对角线的中点，点M、P在平面α上的射影分别是上、下底面对角线的4分点，三个射影同在一条直线上，且与这一直线垂直．从而⊥面MNP．

至此，得①④⑤为本题答案．

解法3　 如图建立空间直角坐标系O－xyz，设正方体的棱长为2，则对角线的方向向量可取为

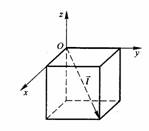
对图①，有

对图②，有

对图③，有

对图④，有

对图⑤，有

综合得本题答案为①④⑤．

从解法3可以看到；应用向量法讨论两直线是否垂直十分方便，操作也比较简单，无须多动脑筋，只需要计算正确即可．

[答案]　 ①④⑤

15．某城市在中心广场建造一个花圃，花圃分为6个部分(如图)．现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花．不同的栽种方法有_____种．(以数字作答)

[分析]　 本题以花圃设计为应用背景，主要考查排列、组合的基础知识，侧重考查乘法原理和加法原理的应用，以及逻辑思维能力和计数能力．

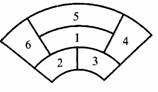
为了正确解答本题，首先必须准确理解题意：抓住花圃布局的要求，看清图形中6个部分的关系；明确每个部分只种同一种颜色的花，相邻部分应种不同颜色的花；而且4种颜色的花都要种上，缺一不可．对这些条件要求，稍有疏忽、遗漏或曲解，都会引致解答出错．其次，应设计好周全而又不出现重复计数的推算程序，关键是推算过程中分步、分类的安排要合理且严密；此外，在每一分步或分类中，计数不出错；最后，乘法原理和加法原理的运用，以及数值计算还得无误，方能得出正确的答数．

采用不同的计数模式和计数程序，伴随出现不同的解法，列举解法供参考．

解法1　 将6个区域分4组，不同组栽种不同颜色的花，同一组栽种同一颜色的花．因为区域1与其它5个区域都有公共边，所以为了栽种方案合乎题意，分在同一组的区域至多只能有2个．因而，由图形可知,不同分组法有且只有5类，如下表(表中数字为区域号)：

	第一组	第二组	第三组	第四组
第一类	1	2	3，5	4，6
第二类	1	2，5	3，6	4
第三类	1	2，5	3	4，6
第四类	1	2，4	3，5	6
第五类	1	2，4	3，6	5

每一类分组法，都有种不同的栽种方法．应用加法原理，得到所有符合题意的不同栽种方法的种数为

解法2 　按区域的顺序，依次安排各区域所栽种的花的颜色：

第1区，可种4色花中的任一种，有4种不同的栽种法；

接着，第2区，因与第1区相邻，两区花色必须不同，所以，第2区只能从3色花中任选一种栽种，有3种不同种法；

跟着，第3区，因与第1、2区都有边界，所以，只有2种不同栽种法；

随后，第4区，与2区无边界，与1、3区都有边界．因此，可分两类情形：

第一类：在第4区中栽种与第2区同一色的花，有1种栽法；至此，只栽种了3种不同颜色的花，因此，第5、6区域，应有一个区域栽种第4种颜色的花，而另一区域可选的花色只有1种(这是因为与之相邻的三个区域，已种上不同颜色的3种花)．从而，在第5、6区域栽花的不同方式有2种；

第二类：在第4区域中栽种与第2区域不同颜色的花，有1种栽法；不过，与第一类不同的是：至此，4种不同颜色的花都被栽种了．往后，第5区域栽花有两种选择：一种是栽与第2区域同色花，紧接着，第6区域有2种栽种方法；第五区域另一种栽花法，是栽种与第2区域不同颜色的花，只有1种选择(因为它不能与1、4区域同色)，紧接着，由于1、2、5三个区域已栽种3种不同颜色的花，故第6区域只有1种栽花的选择．

综合起来，应用乘法原理和加法原理，得合乎题意的不同栽花的方法种数为

N=4×3×2×(1×2+1×2+1×1)

　=120

解法3　 因为区域1与其它5个区域都有公共边，所以当区域1栽种一种颜色的花之后，该颜色的花就不能栽于其它区域．因而可分两步走，考虑如下：

第一步，在区域1中，栽上一种颜色的花，有4种栽法；

第二步，在剩下的五个区域中，栽种其它三种颜色的花．为此，可将2至6号五个区域分成3组，使同一组中的不同区域没有公共边．这样的分组法有且只有5类，如下表(表中数字为区域号)：

	第一组	第二组	第三组
第一类	2	3，5	4，6
第二类	2，4	3，5	6
第三类	2，4	3，6	5
第四类	2，5	3，6	4
第五类	2，5	3	4，6

对每一类分得的3个组，将3种颜色的花分别栽于各组，共有种栽法．

应用乘法原理和加法原理，得合乎题意要求的不同栽种方法的种数为

解法4　 由于第1、2、3区两两都有边界，所以这3个区所栽的花，彼此必须不同颜色．因而，第一步可从4种颜色的花任取3种分别栽在这3个区域上，共有种栽法．其次将另一颜色的花栽于4、5、6三个区中的一个区或两个区，即分为两类情形：

第一类：栽在4、5、6的一个区域中，有3种情形：

情形1：栽于4区，则6区只有一种颜色的花可栽(因为必须不同于4、1、2区的颜色)，进而，5区周边三个区域已栽上3种不同颜色的花，故5区也只有一种颜色的花可栽；

情形2：栽于6区，则与情形1同理，4、5区域分别只有1种颜色可栽；

情形3：栽于5区，由于5、1、2三个区已栽上不同颜色的花，6区只有1种栽法；同理，4区也只有1种栽法．

第二类：栽于4、5、6中的两个区，只有栽于4、6两个区域的一种情形，这时5区有2种栽法(因为5区的周边只有两色花)．

综合起来，应用乘法原理与加法原理，得不同栽种方法的种数为

解法5　 分两类情况考虑：

第1类：第1、2、3、5等四个区域栽种不同颜色的4种花，共有种栽法．对于每一种栽法，第4、6区分别都只有1种颜色的花可栽．

第2类：第1、2、3、5等四个区域栽种不同颜色的3种花，共有种栽法．对于每一种栽法，要么2、5区栽同色花，要么3、5区栽同色花．对于前者，第6区有2种颜色的花可供选栽，第4区只能栽第4种颜色的花；对于后者，第4区有2种颜色的花可供选栽，第6区只能栽第4种颜色的花．即无论何种情形，第4、6区的栽法都是2种．

综合上述情形，应用加法原理与乘法原理，得不同栽种方法的种数为

[答案]　 120