13．已知双曲线(a＞0，b＞0)的半焦距为c，若b²-4ac＜0，则它的离心率的取值的范围是___________.

答.(1,2+) 化b²-4ac＜0＜为c²-a²-4ac＜0，从而变为＜，解关于的一元二次不等式，注意＞1.

12．半径为4的球面上有A、B、C、D四点，且满足，，，则的最大值为(为三角形的面积)　　　　　　　　　　　　　　　　　　 (C)

　　　 A．8　　　　　　　　　 B．16　　　　　　　　 C．32　　　　　　　　 D．64

答　 易知AB，AC，AD两两互相垂直，进而AB²+AC²+AD²=(2r)²=64．

　　 S_△ABC+S_△ACD+S_△ADB=≤=．

11. 用0，1，2，3四个数字组成没有重复数字的自然数，把这些自然数从小到大排成一数列，则1230是这个数列的　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A．第30项　　　　　 B．第32项　　　　　 C．第33项　　　　　 D．第34项

答：用0，1，2，3四个数字组成没有重复数字的自然数,可分为4类：

⑴一位数，有4个(0也是自然数)；⑵两位数，有个；

⑶三位数，有个；　　 ⑷四位数，比1230小的有1023，1032。

于是，1230是这个数列的第34项。　 选D．

10. 椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点、是它的焦点，长轴长为，焦距为，静放在点的小球(小球的半径不计)，从点沿直线出发，经椭圆壁反弹后第一次回到点时，小球经过的路程是　　　　　　　　　　　　　　　　　　 (　　 )

A．　　　　　　 B．　　 　　C．　　 D．以上答案均有可能

答⑴静放在点的小球(小球的半径不计)从点沿直线出发，经椭圆壁右顶点反弹后第一次回到点时，小球经过的路程是，则选B；

⑵静放在点的小球(小球的半径不计)从点沿直线出发，经椭圆壁左顶点反弹后第一次回到点时，小球经过的路程是，则选C；

⑶静放在点的小球(小球的半径不计)从点沿直线出发，经椭圆壁非左右顶点反弹后第一次回到点时，小球经过的路程是，则选A。

于是三种情况均有可能，故选D。

9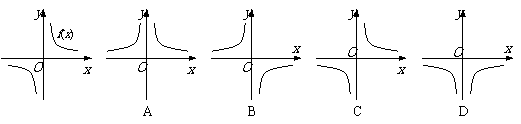． 函数的图象如图所示，则导函数的图象大致是　　　　　　　　　　 (D)

　　　 答　 由的图象及的意义知，在x＞0时，为单调递增函数且＜0；在x＜0时，为单调递减函数且＜0．

8． 已知等比数列的首项为8，是其前n项的和，某同学经计算得S₂=20，S₃=36，S₄=65，后来该同学发现了其中一个数算错了，则该数为　　　　 　　　　　　　　　(C)

　　　 A． S₁　　　　　　　　 B． S₂　　　　 　 C． S₃　 　　　　　　 D． S₄

　　　 　　　　　　　　　 答　 显然S₁是正确的．假设后三个数均未算错，则a₁=8，a₂=12，a₃=16，a₄=29，可知a₂²≠a₁a₃，故S₂、S₃中必有一个数算错了．若S₂算错了，则a₄=29=a₁q³，，显然S₃=36≠8(1+q+q²)，矛盾．只可能是S₃算错了，此时由a₂=12得，a₃=18，a₄=27，S₄=S₂+18+27=65，满足题设．

7． 设函数，若，则下列不等式必定成立的是　 　 (B)

　　　　　　　　　　　　　　　　 A． 　　　 B． 　　　　　　 C． 　　　 D．

　　　 答　 易知，且当x∈时，为增函数．又由，得

，故 |，于是．

6． 已知函数在上是减函数，则实数a的取值范围为　　　　 (D)

　　 A. (5，+∞)　 　 B. (3，+∞)　　 C. (-∞，3)　　　 D.

　　　 答　 定义域为．而函数在时为增函数，故的单调减区间为，从而 ．

5. 给定集合，定义 .若 ，则

　 集合 　中的所有元素之和为　　　　　　　　　　　　　 　　　(A)

　 　A.　 15　　　　　　　　 B.　 14　　　　　　　 C. 　27　　　　　　 D.　 -14

答A※B={3，2，1，4，5}，元素和为15．

4. 设为平面上以 为顶点的三角形区域(　包括边界 ),则　 的最大值和最小值分别为　　　　　　　　　　　　　　　 (A)

　 　A.　 14 , -18　　　　　　 B.　 -14 , -18　　　　 C.　 18 , 14　　　　　 D.　 18 , -14

　 答：画出示意图，易知：当动直线过时，取最大值；当动直线过时，取最小值.