
2.动量观点:动量:p=mv=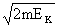 冲量:I = F t
冲量:I = F t
动量定理:内容:物体所受合外力的冲量等于它的动量的变化。
公式: F合t = mv’一mv (解题时受力分析和正方向的规定是关键)
I=F合t=F1t1+F2t2+---= p=P末-P初=mv末-mv初
p=P末-P初=mv末-mv初
动量守恒定律:内容、守恒条件、不同的表达式及含义: ;
; ;
;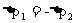
P=P′ (系统相互作用前的总动量P等于相互作用后的总动量P′)
ΔP=0 (系统总动量变化为0)
如果相互作用的系统由两个物体构成,动量守恒的具体表达式为
P1+P2=P1′+P2′ (系统相互作用前的总动量等于相互作用后的总动量)
m1V1+m2V2=m1V1′+m2V2′
ΔP=-ΔP' (两物体动量变化大小相等、方向相反)
实际中应用有:m1v1+m2v2= ; 0=m1v1+m2v2 m1v1+m2v2=(m1+m2)v共
; 0=m1v1+m2v2 m1v1+m2v2=(m1+m2)v共
原来以动量(P)运动的物体,若其获得大小相等、方向相反的动量(-P),是导致物体静止或反向运动的临界条件。即:P+(-P)=0
注意理解四性:系统性、矢量性、同时性、相对性
解题步骤:选对象,划过程;受力分析。所选对象和过程符合什么规律?用何种形式列方程;(先要规定正方向)求解并讨论结果。
1.力的三种效应:
力的瞬时性(产生a)F=ma、 运动状态发生变化
运动状态发生变化 牛顿第二定律
牛顿第二定律
时间积累效应(冲量)I=Ft、 动量发生变化
动量发生变化 动量定理
动量定理
空间积累效应(做功)w=Fs 动能发生变化
动能发生变化 动能定理
动能定理
10.波动模型:特点:传播的是振动形式和能量,介质中各质点只在平衡位置附近振动并不随波迁移。
①各质点都作受迫振动, ②起振方向与振源的起振方向相同, ③离源近的点先振动,
④没波传播方向上两点的起振时间差=波在这段距离内传播的时间⑤波源振几个周期波就向外传几个波长。波从一种介质传播到另一种介质,频率不改变, 波速v=s/t=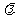 /T=
/T=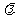 f
f
波速与振动速度的区别 波动与振动的区别:波的传播方向 质点的振动方向(同侧法)
质点的振动方向(同侧法)
知波速和波形画经过Δt后的波形(特殊点画法和去整留零法)
动量守恒:
内容:相互作用的物体系统,如果不受外力,或它们所受的外力之和为零,它们的总动量保持不变。
(研究对象:相互作用的两个物体或多个物体所组成的系统)
守恒条件:①系统不受外力作用。 (理想化条件)
②系统受外力作用,但合外力为零。
③系统受外力作用,合外力也不为零,但合外力远小于物体间的相互作用力。
④系统在某一个方向的合外力为零,在这个方向的动量守恒。
⑤全过程的某一阶段系统受合外力为零,该阶段系统动量守恒,
即:原来连在一起的系统匀速或静止(受合外力为零),分开后整体在某阶段受合外力仍为零,可用动量守恒。
不同的表达式及含义: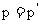 ;
;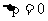 ;
; (各种表达式的中文含义)
(各种表达式的中文含义)
实际中有应用:m1v1+m2v2= ; 0=m1v1+m2v2 m1v1+m2v2=(m1+m2)v共
; 0=m1v1+m2v2 m1v1+m2v2=(m1+m2)v共
注意理解四性:系统性、矢量性、同时性、相对性
系统性:研究对象是某个系统、研究的是某个过程
矢量性:不在同一直线上时进行矢量运算;在同一直线上时,取正方向,引入正负号转化为代数运算。
同时性:v1、v2是相互作用前同一时刻的速度,v1'、v2'是相互作用后同一时刻的速度。
同系性:各速度必须相对同一参照系
解题步骤:选对象,划过程;受力分析.所选对象和过程符合什么规律?用何种形式列方程(先要规定正方向)求解并讨论结果。
历年高考中涉及动量守量模型题:
|
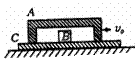
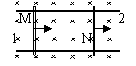
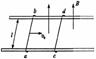
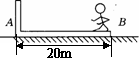
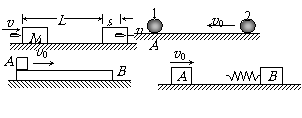
一质量为M的长木板静止在光滑水平桌面上.一质量为m的小滑块以水平速度v0从长木板的一端开始在木板上滑动,直到离开木板.滑块刚离开木板时速度为V0/3,若把此木板固定在水平面上,其它条件相同,求滑块离开木板时速度? |
  |
 |
|
1996年全国广东(24题) |
1995年全国广东(30题压轴题) 1997年全国广东(25题轴题12分) |
1998年全国广东(25题轴题12分) |
|
试在下述简化情况下由牛顿定律导出动量守恒定律的表达式:系统是两个质点,相互作用力是恒力,不受其他力,沿直线运动要求说明推导过程中每步的根据,以及式中各符号和最后结果中各项的意义。 |
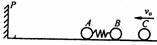 |
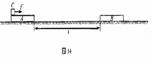
质量为M的小船以速度V0行驶,船上有两个质量皆为m的小孩a和b,分别静止站在船头和船尾. 现小孩a沿水平方向以速率v(相对于静止水面)向前跃入水中,然后小孩b沿水平方向以同一速率v(相对于静止水面)向后跃入水中. 求小孩b跃出后小船的速度. |
|
1999年全国广东(20题12分) |
2000年全国广东(22压轴题) |
2001年广东河南(17题12分) |
 |
  |
  |
|
2002年广东(19题) |
2003年广东(19、20题) |
2004年广东(15、17题) |
 |
  |
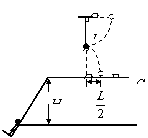 |
|
2005年广东(18题) |
2006年广东(16、18题) |
2007年广东(17题) |
|
其它的碰撞模型: |
||
       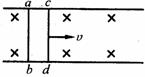 |
碰撞模型:特点?和注意点:
①动量守恒;②碰后的动能不可能碰前大;
③对追及碰撞,碰后后面物体的速度不可能大于前面物体的速度。
m1v1+m2v2= (1) (1) 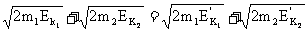 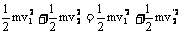 (2 ) (2 )
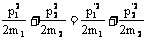 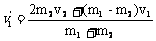 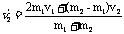 记住这个结论给解综合题带来简便。通过讨论两质量便可。 |
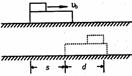
“一动一静”弹性碰撞规律:即m2v2=0 ; =0 代入(1)、(2)式 =0 代入(1)、(2)式 动量守恒:m1v1+m2v2=m1v1'+m2v2' 动能守恒: 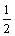 m1v12+ m1v12+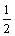 m2v22= m2v22=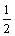 m1v1' 2+ m1v1' 2+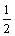 m2v2' 2 m2v2' 2联立可解:v1'= 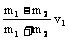 (主动球速度下限) v2'= (主动球速度下限) v2'= (被碰球速度上限) (被碰球速度上限)讨论(1): 当m1>m2时,v1'>0,v2'>0 v1′与v1方向一致; 当m1>>m2时,v1'≈v1,v2'≈2v1 (高射炮打蚊子) 当m1=m2时,v1'=0,v2'=v1 即m1与m2交换速度 当m1<m2时,v1'<0(反弹),v2'>0 v2′与v1同向;当m1<<m2时,v1'≈-v1,v2'≈0 (乒乓球撞铅球) 讨论(2): 被碰球2获最大速度、最大动量、最大动能的条件为 A.初速度v1一定,当m1>>m2时,v2'≈2v1 B.初动量p1一定,由p2'=m2v2'=  ,可见,当m1<<m2时,p2'≈2m1v1=2p1 ,可见,当m1<<m2时,p2'≈2m1v1=2p1C.初动能EK1一定,当m1=m2时,EK2'=EK1 一动静的完全非弹性碰撞。(子弹打击木块模型)是高中物理的重点。 特点:碰后有共同速度,或两者的距离最大(最小)或系统的势能最大等等多种说法. mv0+0=(m+M) 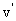
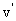 = =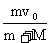 (主动球速度上限,被碰球速度下限) (主动球速度上限,被碰球速度下限)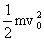 = =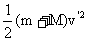 +E损 E损= +E损 E损=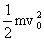 一 一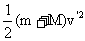 = =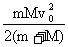 由上可讨论主动球、被碰球的速度取值范围  <v主< <v主<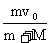 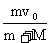 <v被< <v被< 讨论:①E损 可用于克服相对运动时的摩擦力做功转化为内能 E损=fd相= 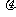 mg·d相= mg·d相=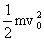 一 一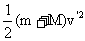 = =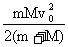  d相= d相=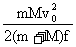 = =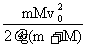 ②也可转化为弹性势能;③转化为电势能、电能发热等等;(通过电场力或安培力做功) |
|
子弹打木块模型:物理学中最为典型的碰撞模型 (一定要掌握) 子弹击穿木块时,两者速度不相等;子弹未击穿木块时,两者速度相等.这两种情况的临界情况是:当子弹从木块一端到达另一端,相对木块运动的位移等于木块长度时,两者速度相等. 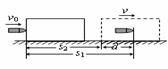 例题:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。 例题:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。解析:子弹和木块最后共同运动,相当于完全非弹性碰撞。 从动量的角度看,子弹射入木块过程中系统动量守恒: 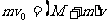 从能量的角度看,该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f,设子弹、木块的位移大小分别为s1、s2,如图所示,显然有s1-s2=d 对子弹用动能定理: 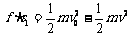 …………………………………① …………………………………①对木块用动能定理: 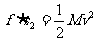 …………………………………………② …………………………………………②①、②相减得: 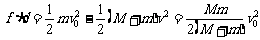 ………………③ ………………③③式意义:fžd恰好等于系统动能的损失;根据能量守恒定律,系统动能的损失应该等于系统内能的增加;可见 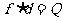 ,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。 ,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。 由上式不难求得平均阻力的大小:  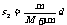 至于木块前进的距离s2,可以由以上②、③相比得出: 至于木块前进的距离s2,可以由以上②、③相比得出:从牛顿运动定律和运动学公式出发,也可以得出同样的结论。试试推理。 由于子弹和木块都在恒力作用下做匀变速运动,位移与平均速度成正比: 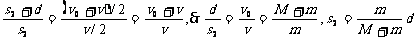 一般情况下 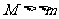 ,所以s2<<d。这说明在子弹射入木块过程中木块的位移很小,可以忽略不计。这就为分阶段处理问题提供了依据。象这种运动物体与静止物体相互作用,动量守恒,最后共同运动的类型, ,所以s2<<d。这说明在子弹射入木块过程中木块的位移很小,可以忽略不计。这就为分阶段处理问题提供了依据。象这种运动物体与静止物体相互作用,动量守恒,最后共同运动的类型,全过程动能的损失量可用公式: 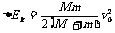 ………………………………④ ………………………………④当子弹速度很大时,可能射穿木块,这时末状态子弹和木块的速度大小不再相等,但穿透过程中系统动量仍然守恒,系统动能损失仍然是ΔEK= f žd(这里的d为木块的厚度),但由于末状态子弹和木块速度不相等,所以不能再用④式计算ΔEK的大小。 做这类题目时一定要画好示意图,把各种数量关系和速度符号标在图上,以免列方程时带错数据。 以上所列举的人、船模型的前提是系统初动量为零。如果发生相互作用前系统就具有一定的动量,那就不能再用m1v1=m2v2这种形式列方程,而要利用(m1+m2)v0= m1v1+ m2v2列式。 特别要注意各种能量间的相互转化 |
9.单摆模型:T=2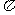
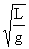 (类单摆) 利用单摆测重力加速度
(类单摆) 利用单摆测重力加速度
8.弹簧振子模型:F=-Kx (X、F、a、v、A、T、f、EK、EP等量的变化规律)水平型 竖直型
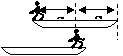
7.人船模型:一个原来处于静止状态的系统,在系统内发生相对运动的过程中,
在此方向遵从动量守恒:mv=MV
ms=MS
s+S=d  s=
s=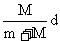 M/m=Lm/LM
M/m=Lm/LM
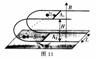
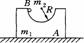
载人气球原静止于高h的高空,气球质量为M,人的质量为m.若人沿绳梯滑至地面,则绳梯至少为多长?

6.碰撞模型:特点,①动量守恒;②碰后的动能不可能比碰前大;
③对追及碰撞,碰后后面物体的速度不可能大于前面物体的速度。
◆弹性碰撞:m1v1+m2v2= (1)
(1) 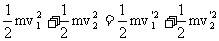 (2 )
(2 )
◆一动一静且二球质量相等的弹性正碰:速度交换
大碰小一起向前;质量相等,速度交换;小碰大,向后返。
◆一动一静的完全非弹性碰撞(子弹打击木块模型)
mv0+0=(m+M)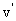
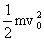 =
=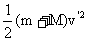 +E损
+E损
E损=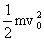 一
一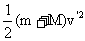 =
=
E损 可用于克服相对运动时的摩擦力做功转化为内能E损=fd相=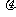 mg·d相=
mg·d相=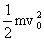 一
一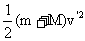
5.超重失重模型
系统的重心在竖直方向上有向上或向下的加速度(或此方向的分量ay)
向上超重(加速向上或减速向下)F=m(g+a);向下失重(加速向下或减速上升)F=m(g-a)
难点:一个物体的运动导致系统重心的运动
1到2到3过程中 (1、3除外)超重状态
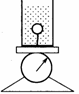
 绳剪断后台称示数
绳剪断后台称示数
系统重心向下加速
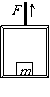
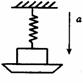
 斜面对地面的压力?
斜面对地面的压力?
地面对斜面摩擦力?
导致系统重心如何运动?

铁木球的运动
用同体积的水去补充
4.轻绳、杆模型
 绳只能受拉力,杆能沿杆方向的拉、压、横向及任意方向的力。
绳只能受拉力,杆能沿杆方向的拉、压、横向及任意方向的力。
杆对球的作用力由运动情况决定
只有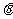 =arctg(
=arctg(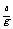 )时才沿杆方向
)时才沿杆方向
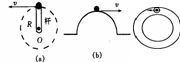 最高点时杆对球的作用力;最低点时的速度?,杆的拉力?
最高点时杆对球的作用力;最低点时的速度?,杆的拉力?
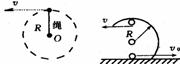 若小球带电呢?
若小球带电呢?
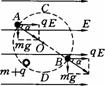

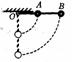 假设单B下摆,最低点的速度VB=
假设单B下摆,最低点的速度VB=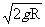
 mgR=
mgR=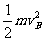
整体下摆2mgR=mg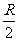 +
+
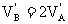

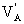 =
=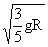 ;
; 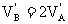 =
=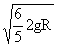 > VB=
> VB=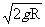
所以AB杆对B做正功,AB杆对A做负功
若 V0<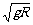 ,运动情况为先平抛,绳拉直沿绳方向的速度消失
,运动情况为先平抛,绳拉直沿绳方向的速度消失
即是有能量损失,绳拉紧后沿圆周下落机械能守恒。而不能够整个过程用机械能守恒。
求水平初速及最低点时绳的拉力?
换为绳时:先自由落体,在绳瞬间拉紧(沿绳方向的速度消失)有能量损失(即v1突然消失),再v2下摆机械能守恒
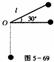
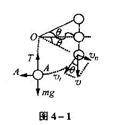 例:摆球的质量为m,从偏离水平方向30°的位置由静释放,设绳子为理想轻绳,求:小球运动到最低点A时绳子受到的拉力是多少?
例:摆球的质量为m,从偏离水平方向30°的位置由静释放,设绳子为理想轻绳,求:小球运动到最低点A时绳子受到的拉力是多少?
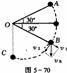
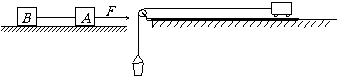
2.连接体模型是指运动中几个物体叠放在一起、或并排在一起、或用细绳、细杆联系在一起的物体组。解决这类问题的基本方法是整体法和隔离法。
整体法是指连接体内的物体间无相对运动时,可以把物体组作为整体,对整体用牛二定律列方程
隔离法是指在需要求连接体内各部分间的相互作用(如求相互间的压力或相互间的摩擦力等)时,把某物体从连接体中隔离出来进行分析的方法。


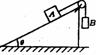

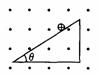
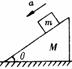
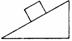 3斜面模型 (搞清物体对斜面压力为零的临界条件)
3斜面模型 (搞清物体对斜面压力为零的临界条件)
 斜面固定:物体在斜面上情况由倾角和摩擦因素决定
斜面固定:物体在斜面上情况由倾角和摩擦因素决定
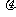 =tg
=tg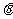 物体沿斜面匀速下滑或静止
物体沿斜面匀速下滑或静止 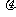 > tg
> tg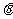 物体静止于斜面
物体静止于斜面
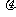 < tg
< tg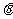 物体沿斜面加速下滑a=g(sin
物体沿斜面加速下滑a=g(sin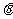 一
一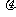 cos
cos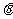 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com