22、(2009安徽卷理)(本小题满分12分)

　 某地有A、B、C、D四人先后感染了甲型H1N1流感，其中只有A到过疫区.B肯定是受A感染的.对于C，因为难以断定他是受A还是受B感染的，于是假定他受A和受B感染的概率都是.同样也假定D受A、B和C感染的概率都是.在这种假定之下，B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).

本小题主要考查古典概型及其概率计算，考查取有限个值的离散型随机变量及其分布列和均值的概念，通过设置密切贴近现实生活的情境，考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。

解　 随机变量X的分布列是

X	1	2	3
P

X的均值为

附：X的分布列的一种求法

共有如下6种不同的可能情形，每种情形发生的概率都是：

①	②	③	④	⑤	⑥
A-B-C-D	A-B-C └D	A-B-C └D	A-B-D └C	A-C-D └B

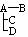在情形①和②之下，A直接感染了一个人；在情形③、④、⑤之下，A直接感染了两个人；在情形⑥之下，A直接感染了三个人。

21、(2009山东卷理)(本小题满分12分)

在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3

分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第

三次，某同学在A处的命中率q为0.25，在B处的命中率为q，该同学选择先在A

处投一球，以后都在B处投，用表示该同学投篮训练结束后所得的总分，其分布列

为

	0	2	3	4	5
p	0.03	P1	P2	P3	P4

(1)求q的值；　 　

(2)求随机变量的数学期望E;

(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。

解 (1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25,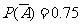, P(B)= q,.

根据分布列知: =0时=0.03,所以

，q=0.8.

(2)当=2时, P₁= 　　　

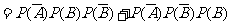=0.75 q( )×2=1.5 q( )=0.24

当=3时, P₂ ==0.01,

当=4时, P₃==0.48,

当=5时, P₄=

=0.24

所以随机变量的分布列为

	0	2	3	4	5
p	0.03	0.24	0.01	0.48	0.24

随机变量的数学期望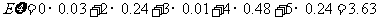

(3)该同学选择都在B处投篮得分超过3分的概率为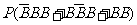

;

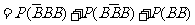
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.

由此看来该同学选择都在B处投篮得分超过3分的概率大.

20、(2009北京卷理)(本小题共13分)

某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，遇到红灯时停留的时间都是2min.

(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率；

(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间的分布列及期望.

解　 (Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A，因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯，在第三个路口遇到红灯”，所以事件A的概率为.

(Ⅱ)由题意，可得可能取的值为0，2，4，6，8(单位：min).

事件“”等价于事件“该学生在路上遇到次红灯”(0，1，2，3，4)，

∴，

∴即的分布列是

	0	2	4	6	8

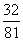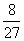∴的期望是.

19、(2009北京卷文)(本小题共13分)

某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，遇到红灯时停留的时间都是2 min.

(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率；

(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.　　　　　　　

解(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A，因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯，在第三个路口遇到红灯”，所以事件A的概率为.

(Ⅱ)设这名学生在上学路上因遇到红灯停留的总时间至多是4min为事件B，这名学

生在上学路上遇到次红灯的事件.

则由题意，得，

.

由于事件B等价于“这名学生在上学路上至多遇到两次红灯”，

∴事件B的概率为.

18、(2009浙江卷理)(本题满分14分)在这个自然数中，任取个数．

　(I)求这个数中恰有个是偶数的概率；

　(II)设为这个数中两数相邻的组数(例如：若取出的数为，则有两组相邻的数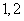和，此时的值是)．求随机变量的分布列及其数学期望．

解(I)记“这3个数恰有一个是偶数”为事件A，则； 　　

(II)随机变量的取值为的分布列为

	0	1	2
P

所以的数学期望为 　　　

17．(2009重庆卷文)从一堆苹果中任取5只，称得它们的质量如下(单位：克)125　 124　 121　 123　 127则该样本标准差　　　　　　 (克)(用数字作答)．

[解析]因为样本平均数，则样本方差所以

答案　 2

16.(2009福建卷文)点A为周长等于3的圆周上的一个定点，若在该圆周上随机取一点B，则劣弧AB的长度小于1的概率为　　　　　　　 。

[解析]如图可设,则,根据几何概率可知其整体事件是其周长，则其概率是。　 　

答案　

0.5，则三人都达标的概率是　　　　　　 ，三人中至少有一人达标的概率是　　　　　 。

[解析]三人均达标为0.8×0.6×0.5=0.24,三人中至少有一人达标为1-0.24=0.76

答案　 0.24　　　 0.76

15.(2009湖北卷文)甲、乙、丙三人将参加某项测试，他们能达标的概率分别是0.8、0.6、

14.(2009江苏卷)某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮练习，每人投10次，投中的次数如下表：

则以上两组数据的方差中较小的一个为=　 　　.

[解析] 考查统计中的平均值与方差的运算。

甲班的方差较小，数据的平均值为7，

故方差 　

答案