
5.函数极限有哪些性质
和数列极限性质完全相仿,函数极限也具有以下几个性质:
性质1.若 ,且A>B,则存在δ>0,使当
,且A>B,则存在δ>0,使当 时,
时,
f(x)>g(x).
证明:取 那么存在
那么存在 当
当 时,有
时,有 ;同时又存在
;同时又存在 ,当
,当 时,有
时,有 ,现在,令
,现在,令 ,那么当
,那么当 时,就有
时,就有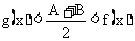
性质2.若 且存在δ>0,使当
且存在δ>0,使当 时,f(x)<g(x),则A≤B.
时,f(x)<g(x),则A≤B.
性质3.若 而A>B(A<B),则存在δ>0,使当
而A>B(A<B),则存在δ>0,使当 时,f(x)>B(f(x)<B).
时,f(x)>B(f(x)<B).
性质4.若 则A=B,这说明了函数极限的惟一性.
则A=B,这说明了函数极限的惟一性.
证明:采用反证法,如果A≠B,不妨设A>B,由性质1知道,存在δ>0,当 时,有f(x)>f(x)矛盾,这就证明了A=B
时,有f(x)>f(x)矛盾,这就证明了A=B
性质5.若存在δ>0,使当 时,f(x)≤g(x)≤h(x),并且
时,f(x)≤g(x)≤h(x),并且
 则
则
性质6.(局部有界性)若 ,则存在着δ>0,使得f(x)在区间
,则存在着δ>0,使得f(x)在区间 和
和 内有界,亦即在不等式
内有界,亦即在不等式 所表示的区间内有界.
所表示的区间内有界.
[注:若函数f(x)在某个区间Z内满足A≤f(x)≤B,其中A,B是两个常数,我们称f(x)在Z内有界,并称A是f(x)在Z内的下界,B是f(x)在Z内的上界.显然,对任何α>0,A-α都是f(x)的下界,同样对任何β>0,B+β都是f(x)的上界.这个定义也可以这样叙述:设函数f(x)在某个区间Z内满足|f(x)|≤M,其中M是一个正实数,我们就称f(x)在Z内有界.以上两种说法显然是等价的.]
证明:取-个固定的ε,譬如说取ε=1,由 知道,存在δ>0,当
知道,存在δ>0,当 时,有A-1<f(x)<A+1,这就证明了f(x)在
时,有A-1<f(x)<A+1,这就证明了f(x)在 和
和 内有界.
内有界.
要注意的是,由极限存在,只能断定函数在相应的某个去心邻域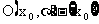 内有界,而不能断定它在整个定义域内有界.例如
内有界,而不能断定它在整个定义域内有界.例如 ,它的定义域是(-∞,1)和(1,+∞),由前面的例子知道
,它的定义域是(-∞,1)和(1,+∞),由前面的例子知道 .根据性质6,存在某个δ>0,在(1-δ,1)和(1,1+δ)内,
.根据性质6,存在某个δ>0,在(1-δ,1)和(1,1+δ)内, 有界.但是这个函数在它的定义域内有
有界.但是这个函数在它的定义域内有 ,它的图形是一条抛物线,但除去x=1,可见在(-∞,1)和(1,+∞)内是无界的.
,它的图形是一条抛物线,但除去x=1,可见在(-∞,1)和(1,+∞)内是无界的.
4.数列的收敛判别法有哪法?
方法1.若存在自然数N,当n>N,总有 ,且
,且 ,则
,则
[注:方法1被称为夹挤定理.]
例1 计算

思路启迪
 只要找到两个数列
只要找到两个数列 与
与 ,使
,使 则
则
规范解法 


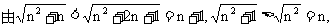


方法2.单调有界数列存在极限.
例2 证明数列 收敛,并求它的极限.
收敛,并求它的极限.
思路启迪 首先对于这种随n的增大,数列的项有规律变化的情况可以用数学归纳法证明该数列单调并且有界.这样该数列必存在极限.可以设极限为 ,则根据第n+1项与第n项的关系列出关于
,则根据第n+1项与第n项的关系列出关于 的等式就可以求出
的等式就可以求出 .
.
规范证法 设 有
有 ,用归纳法证明数列
,用归纳法证明数列 是单调增加的,又是有上界的.显然
是单调增加的,又是有上界的.显然 ,设
,设 (k是自然数)有
(k是自然数)有 ,即
,即 ,则数列
,则数列 是单调增加的.显然,当n=1时,有
是单调增加的.显然,当n=1时,有 .设n=k时,有
.设n=k时,有 .当n=k+1时,也有
.当n=k+1时,也有 ,即数列
,即数列 是有上界的.由于数
是有上界的.由于数 是单调增加的并且有上界,所以数则
是单调增加的并且有上界,所以数则 收敛.设
收敛.设 ,已知
,已知 ,有
,有 即
即 ,得
,得 ,由
,由 可知,
可知, 不能是负数,则数列
不能是负数,则数列 的极限是
的极限是
3.什么是单调有界数列?
设 是一个数列,如果
是一个数列,如果 我们就说这个数列是单调增加(上升)的.如果
我们就说这个数列是单调增加(上升)的.如果 我们就说这个数列是单调减少(下降)的.例如
我们就说这个数列是单调减少(下降)的.例如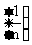 就是一个单调减少的数列.如果在上面数列中等号都不成立,就称它是严格单调增加或严格单调减少的.
就是一个单调减少的数列.如果在上面数列中等号都不成立,就称它是严格单调增加或严格单调减少的.
2.什么是有界数列?
定义:若存在两个数A,B(设A<B),数列 中的每一项都在闭区间[A,B]内,亦即
中的每一项都在闭区间[A,B]内,亦即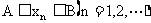 ,则称
,则称 为有界数列.这时A称为它的下界,B称为它的上界.关于有界数列有下面几点说明.
为有界数列.这时A称为它的下界,B称为它的上界.关于有界数列有下面几点说明.
(1)如果B是数列 的上界,那么B+1,B+2,B+α(α>0)都是
的上界,那么B+1,B+2,B+α(α>0)都是 的上界.这表明上界并不是惟一的,下界也是如此.
的上界.这表明上界并不是惟一的,下界也是如此.
(2)对于数列 ,如果存在正整数N,当n>N时,总有
,如果存在正整数N,当n>N时,总有 ,我们就说数列
,我们就说数列 往后有界.要注意,往后有界一定是有界的,这是因为在N项之前只有有限多个数
往后有界.要注意,往后有界一定是有界的,这是因为在N项之前只有有限多个数 在这有限个数中必有最大的数和最小的数,设
在这有限个数中必有最大的数和最小的数,设 ,
,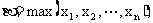 那么min(A,α)和max(B,β)就是整个数列
那么min(A,α)和max(B,β)就是整个数列 的下界和上界.
的下界和上界.
(3)有界数列也可以这样叙述:若存在一个正数M,使得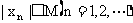 ,就称
,就称 是有界数列.或者也可以这么说,若存在原点O的一个M邻域O(O,M),使得所有
是有界数列.或者也可以这么说,若存在原点O的一个M邻域O(O,M),使得所有 ,就称
,就称 是有界数列,这种叙述和上面所给出的定义显然是等价的.
是有界数列,这种叙述和上面所给出的定义显然是等价的.
12.设 ,则
,则




32.设函数f(x)在[a,b]-上连续,f(x)>0,则 在[a,b]上存在最大值和最小值. ( )
在[a,b]上存在最大值和最小值. ( )
31.在闭区间上连续的函数,在该区间上定能取到最大值或最小值. ( )
30.若f(x)在(a,b)内连续,则f(x)在该区间内必取得最大值和最小值. ( )
26.在某变化过程中,若 有极限,
有极限, 无极限,则在该过程中,
无极限,则在该过程中,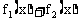 必无极限. ( )
必无极限. ( )



25.在某变化过程中,若 与
与 极限,则在该过程中,
极限,则在该过程中, 必无极限.( )
必无极限.( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com