
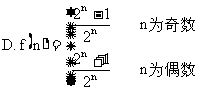
4.数列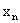 与
与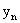 的极限分别为A与B,A≠B,则数列
的极限分别为A与B,A≠B,则数列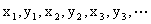 的极限为( )
的极限为( )
A.A B.B C.A+B D.不存在
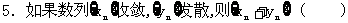
A.可能收敛 B.一定收敛 C.可能发散 D.一定发散
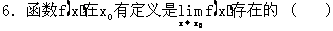
A.充要条件 B.充分条件 C.必要条件 D.无关条件
3.下列数收敛于0有( )
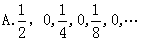
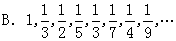
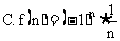
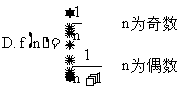
2.下列数列收敛的有( )
A.0.9,0.99,0.999,0.9999,… 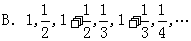
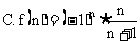
1.下列数列极限存在的有( )
A.10,10,10,… 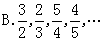


13.求函数极限有哪些方法?
在某一极限过程中,参加极限四则运算的每一个极限都必须有相同的过程,而且每个极限都必须存在(分母不为零)才能运算.
我们通过下面几道题来总结一下求函数极限的方法.
例1 求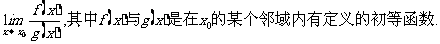
思路启迪 由于f(x)与g(x)是在 的某邻域内有定义的初等函数,所以
的某邻域内有定义的初等函数,所以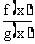 也是在
也是在 的某邻域内有定义的初等函数.根据初等函数的连续性可求出该极限.
的某邻域内有定义的初等函数.根据初等函数的连续性可求出该极限.
规范解法 由初等函数的连续性,得

例2 求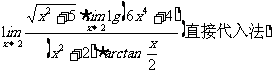
思路启迪 由于当x→2时,分子、分母的极限都存在,并且分母的极限不为0,所以可以将x→2直接代入分子、分母,根据初等函数的连续性,分别求出分子分母的极限,再求商即可.
规范解法 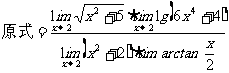
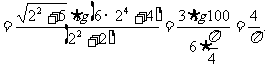
例3 求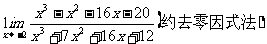
思路启迪 由于将x→-2代入分母,可得分母极限为0,所以此题不能用直接入法.根据观察,可以将分子分母分解因式,都可以分解出极限为0的x+2,约去公因式即可求极限了.
规范解法 
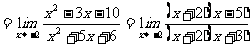
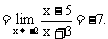
例4 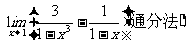
思路启迪 因为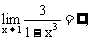
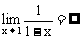 ,所以不能直接用求函数极限差的运算法则,可将函数通分变形后再求极限.
,所以不能直接用求函数极限差的运算法则,可将函数通分变形后再求极限.
规范解法 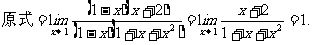
例5 求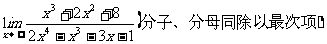
思路启迪 由于分子,分母的极限都是无穷大,所以分子、分母同除以最高次项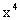 ,使分子、分母的极限都存在.
,使分子、分母的极限都存在.
规范解法 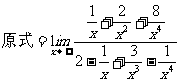
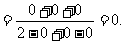
点评 一般地
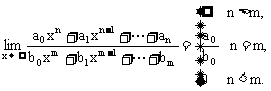
例6 求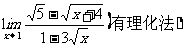
思路启迪 求函数极限时,若碰到分子,分母中有根号的情形,经常会把分子或分母有理化,使原极限可求.
规范解法 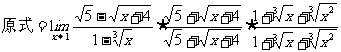

例7 求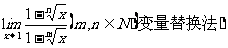
思路启迪 分子,分母中分别有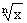 ,
,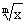 直接求极限不好求,可以采用变量规换的方法,令
直接求极限不好求,可以采用变量规换的方法,令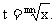
规范解法 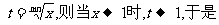
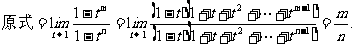
例8 求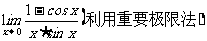
思路启迪 出现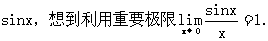
规范解法一 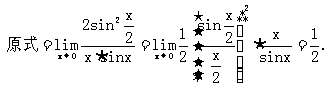
规范解法二 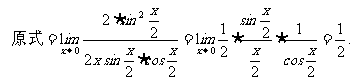
规范解法三 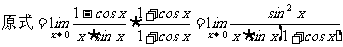
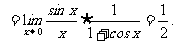
12.什么是函数在一个区间上的连续性?
如果函数f(x)在开区间(a,b)内每一点连续,则称函数f(x)在开区间(a,b)上连续;如果函数f(x)在闭区间[a,b]内每一点(非端点)都连续,且函数f(x)在左端点a右连续,在右端点b左连续,则称函数f(x)在闭区间[a,b]上连续.一般地,对任何-个区间I,如果函数f(x)在区间I内的每一点(非端点)都连续,且当区间I含有端点时,函数f(x)在端点处单侧连续(在左端点指的是右连续,在右端点指的是左连续),则称函数f(x)在区间I上连续.
例如,函数f(x)=sin x在区间(-∞,+∞)内每一点都是连续的,因而可说函数f(x)=sinx在区间(-∞,+∞)上连续.
又如,函数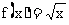 在区间[0,+∞)内的每一点(不包括端点x=0)都是连续的.又在区间的左端点x=0满足
在区间[0,+∞)内的每一点(不包括端点x=0)都是连续的.又在区间的左端点x=0满足 ,则
,则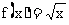 在x=0点右连续,因此可说函数
在x=0点右连续,因此可说函数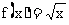 在区间(0,+∞)上连续.利用连续函数的定义和性质,可以证明,-切基本初等函数在它们的定义域内都是连续的.
在区间(0,+∞)上连续.利用连续函数的定义和性质,可以证明,-切基本初等函数在它们的定义域内都是连续的.
计算极限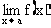 .若已知函数f(x)是初等函数,而a又属于函数f(x)的定义域,则函数f(x)在点a连续,根据连续定义,“
.若已知函数f(x)是初等函数,而a又属于函数f(x)的定义域,则函数f(x)在点a连续,根据连续定义,“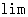 ”与“f”可交换次序,即
”与“f”可交换次序,即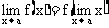 ,于是,计算连续函数f(x)在点a的极限就变成了计算函数f(x)在点a的函数值f(a).
,于是,计算连续函数f(x)在点a的极限就变成了计算函数f(x)在点a的函数值f(a).
例 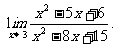
思路启迪 可以先将极限式的分子,分母分解,这就会出现重复项x-3.由于函数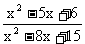 在点3的极限只与3附近点x的函数值变化有关与点3无关,即x≠3或x-3≠0,因此可以消去分子与分母中的公共因式x-3.
在点3的极限只与3附近点x的函数值变化有关与点3无关,即x≠3或x-3≠0,因此可以消去分子与分母中的公共因式x-3.
规范解法

11.什么是函数的连续性?
现实世界中很多变量的变化是连续不断的,如气温、物体运动的路程,金属丝加热时长度的变化等等,都是连续变化的.这种现象反映在数学上就是函数的连续性,它是微积分的又一重要概念.
下面我们先引入函数改变量的概念与记号.
函数改变量(或称函数增量).
定义:设变量t从它的初值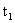 改变到终值
改变到终值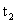 ,终值与初值之差
,终值与初值之差 称为变量t的改变量,
称为变量t的改变量,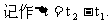
[注:改变量可以是正的,也可以是负的.]
设有函数y=f(x),给自变量x一个改变量△x,当自变量x从 改变到
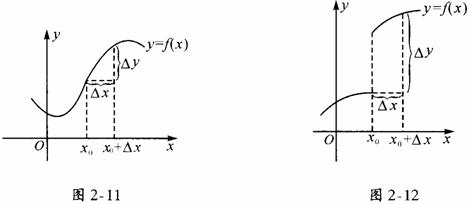
改变到 时,函数y相应的改变量为△y.如图2-10所示,△y为:
时,函数y相应的改变量为△y.如图2-10所示,△y为:

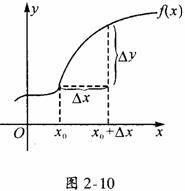
对于函数y=f(x)定义域内一点 ,如果自变量x在点
,如果自变量x在点 处取得极其微小的改变量△x时,函数y相应的改变量△y也极其微小,且当△x趋于0时,△y也趋于0,则称函数y=f(x)在点
处取得极其微小的改变量△x时,函数y相应的改变量△y也极其微小,且当△x趋于0时,△y也趋于0,则称函数y=f(x)在点 处是连续的.如图2-11.而对图2-12来说,在点
处是连续的.如图2-11.而对图2-12来说,在点 处不满足这个条件,所以,它在点
处不满足这个条件,所以,它在点 处不连续.
处不连续.
下面给出函数在一点处连续的定义.
定义:设函数y=f(x)在点 的某个邻域内有定义,如果当自变量x在点
的某个邻域内有定义,如果当自变量x在点 处取得改变量△x趋于0时,函数相应的改变量△y也趋于0,即
处取得改变量△x趋于0时,函数相应的改变量△y也趋于0,即 或写作
或写作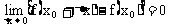 ,则称函数f(x)在点
,则称函数f(x)在点 处连续.
处连续.
例1 证明函数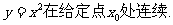
思路启迪 要证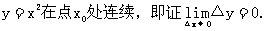
规范证法 当x从 处产生一个改变量△x时,函数
处产生一个改变量△x时,函数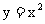 相应改变量为
相应改变量为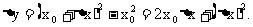 因为
因为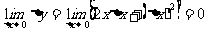 ,所以
,所以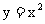 在给定点
在给定点 处连续.
处连续.
在上面的定义中,令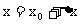 ,则
,则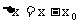 ,那么当
,那么当 时,必有
时,必有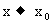 ,且
,且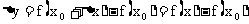 ,因而
,因而 可以写为
可以写为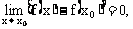 即
即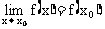 因此,函数在点
因此,函数在点 处连续,也可以如下定义:
处连续,也可以如下定义:
设函数y=f(x)在点 的某个邻域内有定义,如果
的某个邻域内有定义,如果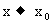 时,函数f(x)的极限存在,而且等于f(x)在点
时,函数f(x)的极限存在,而且等于f(x)在点 处的函数值
处的函数值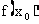 ,即有
,即有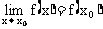 ,则称函数f(x)在点
,则称函数f(x)在点 处连续.
处连续.
因此,求连续函数在某点的极限,只须求出函数在该点的函数值即可.前面例1已证明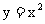 在点
在点 处连续,故有
处连续,故有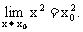
例2 证明正弦函数f(x)=sinx在R上连续.
思路启迪 要证f(x)=sinx在R上连续,只需证明对任意的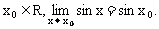
规范证法 对任意ε>0,解不等式
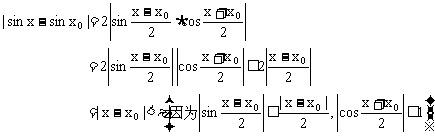
取δ≤ε,于是,对任意ε>0,总存在δ≤ε(其中δ>0),当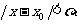 时,有
时,有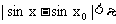 ,即正弦函数sinx在
,即正弦函数sinx在 连续,因为
连续,因为 是R上任意-点,所以正弦函数sinx在R上是连续函数.同理可知,余弦函数cosx在R上也是连续函数.
是R上任意-点,所以正弦函数sinx在R上是连续函数.同理可知,余弦函数cosx在R上也是连续函数.
10.什么是函数两个重要极限?
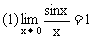
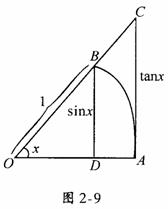
证明:首先证明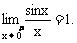 如下图2-9,
如下图2-9, 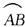 是以点O为心,半径为1的圆弧,过A作圆弧的切线与OB的延长线交于点C.设∠DOB=x(按弧度计算),则
是以点O为心,半径为1的圆弧,过A作圆弧的切线与OB的延长线交于点C.设∠DOB=x(按弧度计算),则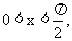 显然,△AOB的面积<扇形AOB的面积<△AOC的面积.即
显然,△AOB的面积<扇形AOB的面积<△AOC的面积.即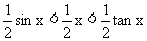 或sinx<x<tanx,以sinx>0除之,得
或sinx<x<tanx,以sinx>0除之,得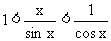 或
或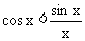 .∵
.∵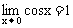 ,
,
∴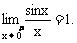 (根据夹挤定理,参看后面知识链接部分第4个问题中的方法1).
(根据夹挤定理,参看后面知识链接部分第4个问题中的方法1).
其次,当x<0时,设x=-y,当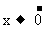 时,有
时,有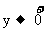 ,则
,则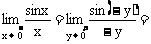
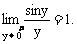
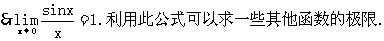
例1 求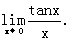
思路启迪 将tanx写成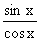 ,代回原式,使之出现
,代回原式,使之出现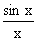 这个重要极限.
这个重要极限.
规范解法

例2 求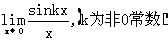
思路启迪 将kx看成一个新变量t,即令t=kx,则x→0时,t→0.
规范解法
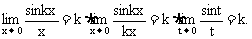
例3 求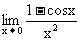
思路启迪 先将1-cosx用半角公式化成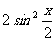 ,就可以利用特殊极限
,就可以利用特殊极限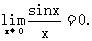
规范解法 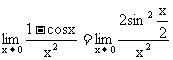
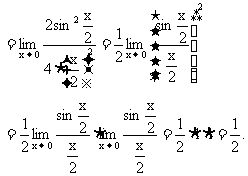
注意:我们在利用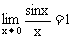 时,一定要注意x的趋向形式,x是趋向于0的,若x是趋向于无穷的或者x是趋向于除0以外的其他值,则该极限等式就不一定成立了.
时,一定要注意x的趋向形式,x是趋向于0的,若x是趋向于无穷的或者x是趋向于除0以外的其他值,则该极限等式就不一定成立了.
下面大家来看另一重要极限
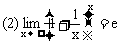
我们先讨论x→+∞的情形.因[x]≤x<[x]+1,[注:“[ ]”是取整数符号,在y=[x]中,对任意的x∈R,对应的y是不超过x的最大整数.例如:[2.5]=2,[3]=3,[0]=0,[-π]=-4,故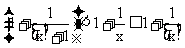 ,而
,而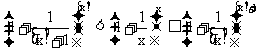 ,但由于
,但由于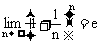 ,而x→+∞时,[x]取正整数值而趋于+∞,所以从
,而x→+∞时,[x]取正整数值而趋于+∞,所以从
 和
和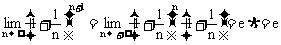
,得到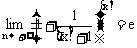 和
和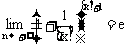 .由极限性质即得到
.由极限性质即得到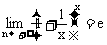 .再证
.再证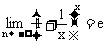 ,作代换x=-y,则
,作代换x=-y,则
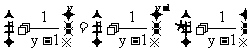 .但x→-∞时,y-1→+∞,上式右端以e为极限,所以左端也以e为极限.证毕.
.但x→-∞时,y-1→+∞,上式右端以e为极限,所以左端也以e为极限.证毕.
例4 求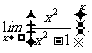
思路启迪 先把极限式变形,使之变成可以利特殊极限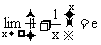 的形式.
的形式.
规范解法 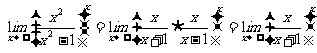
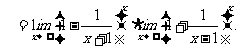


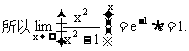
9.怎样计算函数的极限?
要计算函数的极限,需知道函数极限的运算法则,它们的证明完全和数列的情形相仿.
函数极限的四则运算法则:
如果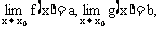 那么
那么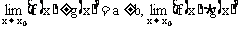
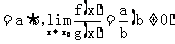 .这些法则对于x→∞时的情况仍然成立.由以上法则易得
.这些法则对于x→∞时的情况仍然成立.由以上法则易得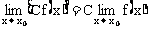 (C是常数),
(C是常数),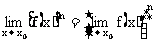 (n是正整数).利用这些法则求下面几个函数的极限.
(n是正整数).利用这些法则求下面几个函数的极限.
例1 求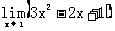
思路启迪 由于该极限中的每一项都存在极限,所以可以用极限四则运算法则中和式的极限等于极限的和来计算.
规范解法 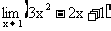

点评 若极限式各项中,有一项或几项的极限不存在,就不能直接利用函数极限的四则运算法则来做.
例2 求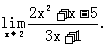
思路启迪 与例1类似.
规范解法 因为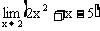
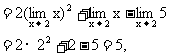
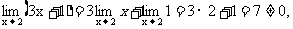
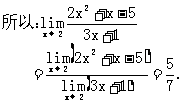
点评 由例1,例2可以看出:若f(x)为多项式函数或当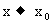 时分母极限不为0的分式函数,根据极限运算法则可以得出
时分母极限不为0的分式函数,根据极限运算法则可以得出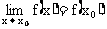
例3 求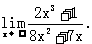
思路启迪 将分子分母同除以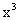 ,使分子分母的极限存在.
,使分子分母的极限存在.
规范解法 将分子分母同除以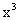 ,得
,得
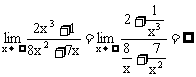
例4 求
思路启迪 将分子有理化,使分子分母极限存在.
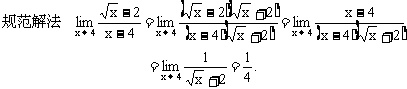
例5 已知
求
思路启迪 要求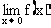 ,应先看其左,右极限,比较两极限是否相同,若相同,则极限为其左,右极限值,若不相同,则极限不存在.
,应先看其左,右极限,比较两极限是否相同,若相同,则极限为其左,右极限值,若不相同,则极限不存在.

8.什么是函数左极限与右极限?
前面讲了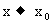 时函数f(x)的极限,在那里x是以任意方式趋于
时函数f(x)的极限,在那里x是以任意方式趋于 的.但是,有时我们还需要知道x仅从
的.但是,有时我们还需要知道x仅从 的左侧
的左侧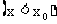 或仅从
或仅从 的右侧
的右侧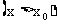 趋于
趋于 时,f(x)的变化趋势.于是,就要引进左极限与右极限的概念.
时,f(x)的变化趋势.于是,就要引进左极限与右极限的概念.
例如,函数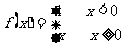 ,图形见图2-8.
,图形见图2-8.
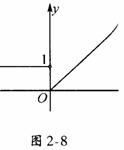
容易观察出,当x从0的左侧趋于0时,f(x)趋于1;而当x从0的右侧趋于0时,f(x)趋于0.我们分别称它是x趋于0时的左极限与右极限.
再考察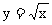 当x趋于0时的极限.由于函数的定义域为[0,+∞)因此只能考察其右极限.对
当x趋于0时的极限.由于函数的定义域为[0,+∞)因此只能考察其右极限.对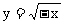 ,由于其定义域为(-∞,0],因此,当x趋于0时,只能考察其左极限.
,由于其定义域为(-∞,0],因此,当x趋于0时,只能考察其左极限.
定义:如果当x从 的左侧
的左侧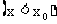 趋于
趋于 时,f(x)以A为极限,即对于任意给定的ε>0,总存在一个正数δ,使
时,f(x)以A为极限,即对于任意给定的ε>0,总存在一个正数δ,使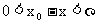 时,
时,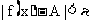 恒成立,则称A为
恒成立,则称A为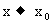 时f(x)的左极限.记作
时f(x)的左极限.记作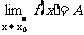 或
或 如果当x从
如果当x从 的右侧
的右侧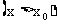 趋于
趋于 时,f(x)以A为极限,即对于任意给定的ε>0,总存在-个正数δ,使当
时,f(x)以A为极限,即对于任意给定的ε>0,总存在-个正数δ,使当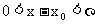 时,|f(x)-A|<ε恒成立,则称A为
时,|f(x)-A|<ε恒成立,则称A为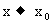 时f(x)的右极限,记作
时f(x)的右极限,记作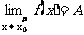 或
或
根据左、右极限的定义,显然可以得到下列定理.
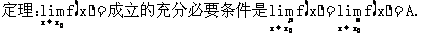
例1 设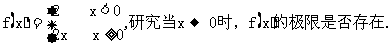
思路启迪 要看当x→0时,f(x)的极限是否存在,就应先求出x→0时f(x)的左、右极限,并看f(x)的左、右极限是否相等.若相等,则极限存在;反之,则极限不存在.
规范解法 当x<0时, ;而当x≥0时,
;而当x≥0时,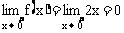 .左、右极限都存在,但不相等.所以,由上面的定理可知,
.左、右极限都存在,但不相等.所以,由上面的定理可知,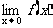 不存在.
不存在.
例2 研究当x→0时,f(x)=|x|的极限.
思路启迪 因为f(x)=|x|,所以应对f(x)分情况讨论,得到f(x)为一个分段函数,再按照例1的方法讨论f(x)的极限.
规范解法  已知
已知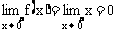 ,可以证明,
,可以证明,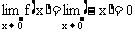 ,所以,由上面的定理得
,所以,由上面的定理得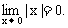
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com