14．给出下列四个命题：

①设R，则且的充要条件是且；

②任意的锐角三角形中，有成立；

③平面上个圆最多将平面分成个部分；

④空间中直角在一个平面上的正投影可以是钝角．

其中真命题的序号是　　　　　　　　　　　 (要求写出所有真命题的序号)．

13．如图3，有一轴截面为正三角形的圆锥形容器，

内部盛水的高度为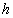，放入一球后，水面恰好与

球相切，则球的半径为　　　　 (用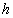表示)．

12．若偶函数在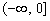内单调递减，则不等式的解集是　　　　 ．

11．据研究，甲、乙两个磁盘受到病毒感染，感染的量(单位：比特数)与时间(单位：秒)的函数关系式分别是和．

显然，当时，甲磁盘受到的病毒感染增长率比乙磁盘受到的病毒感染增长率大．试根据上述事实提炼一个不等式是　　　　　　　　 ．

10．若△的三个内角满足，则等于　　　 ．

9．将编号分别为1，2，3，4，5的五个红球和五个白球排成一排，要求同编号球相邻，但同色球不相邻，则不同排法的种数为　　　　 (用数字作答)．

8．已知点所在的可行域如图2所示．若要使目标函数

取得最大值的最优解有无数多个，则的值为

　 A．4　　　　 B．　　　　 C．　　　　 D．

7．已知向量满足，，且，则等于

A．　　　　　 B．　　　　　 C．　　　　　 D．7

6．公差不为零的等差数列中，，，成等比数列，则其公比为

A．1　　　　　　　 B．2　　　　　　　　 C．3　　　　　　　　 D．4

5．函数在定义域内有

A．最大值　　　　 B．最小值　　　　 C．最大值　　　 D．最小值