
21. (本小题满分14分)
设函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)当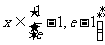 时,不等式
时,不等式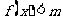 恒成立,求实数
恒成立,求实数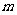 的取值范围;
的取值范围;
(3)关于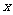 的方程
的方程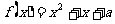 在
在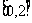 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数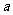 的取值范围.
的取值范围.
20.(本小题满分14分)
如图3,四棱锥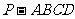 中,
中,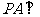 底面
底面 ,
,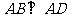 ,
, ,
,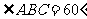 ,
,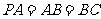 ,
, 是
是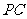 的中点.
的中点.
(1)求证: ;
;
(2)求证: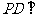 面
面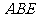 ;
;
 (3)求二面角
(3)求二面角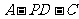 的平面角的正弦值.
的平面角的正弦值.
19.(本题满分14分)
已知圆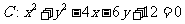 , 点
, 点 ,
,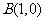 ,求;
,求;
(1)过点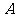 的圆C的切线方程;
的圆C的切线方程;
(2) 点是坐标原点,连结
点是坐标原点,连结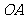 ,
,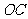 ,求
,求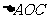 的面积
的面积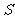 .
.
(3)设动圆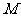 过点
过点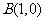 ,且圆心
,且圆心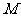 在抛物线
在抛物线 :
: 上,
上,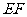 是圆
是圆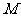 在
在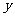 轴上截得的弦,当
轴上截得的弦,当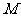 运动时弦长
运动时弦长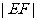 是否为定值?请说明理由.
是否为定值?请说明理由.
18.(本题满分14分)
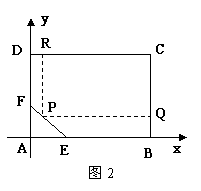 如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
17.(本题满分12分)
数列
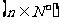 是递增的等比数列,且
是递增的等比数列,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若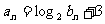 ,求证数列
,求证数列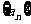 是等差数列;
是等差数列;
(Ⅲ)若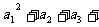 ……
…… ,求
,求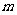 的最大值.
的最大值.
16.(本小题满分12分)
已知向量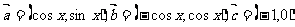 .
.
(1)若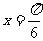 ,求向量
,求向量 的夹角;
的夹角;
(2)已知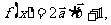 且
且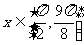 ,当
,当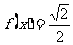 时,求
时,求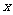 的值.
的值.
(二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计算第一题的得分.
14.(选做题)若不等式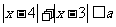 的解集为
的解集为 ,则
,则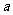 的取值范围是
.
的取值范围是
.
15.(选做题) 若圆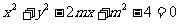 与圆
与圆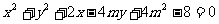 相切,则实数
相切,则实数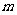 的取值集合是
.
的取值集合是
.
(一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须做答
9.(注:缺题)
10.已知函数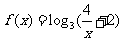 ,则方程
,则方程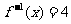 的解是
.
的解是
.
11. 如图,测量河对岸的塔高AB时,可以选与塔底B在同
如图,测量河对岸的塔高AB时,可以选与塔底B在同
一水平面内的两个测点C与D.现测得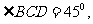
 ,CD=40,并且在点C测得塔顶A的仰角
,CD=40,并且在点C测得塔顶A的仰角
为 则塔高AB为
. (结果用无理数表示)
则塔高AB为
. (结果用无理数表示)
12. 将 的图象向左平移
的图象向左平移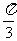 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的 的图象;若函数
的图象;若函数 ,
, 的图象与
的图象与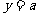 的图象有三个交点且交点的横坐标成等比数列,则
的图象有三个交点且交点的横坐标成等比数列,则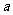 的值为________.
的值为________.
13. 对于任意的两个实数对 (a,b) 和 (c,d),规定:(a,b) = (c,d)当且仅当 a = c,b = d;运算“Ä”为:a,b) Ä (c,d) = (ac-bd,bc + ad);运算“Å”为:(a,b) Å (c,d) = (a + c,b + d),设p、q Î R,若(1,2) Ä (p,q) = (5,0),则 (1,2) Å (p,q) =_________.
8.设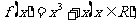 若
若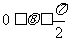 时,
时, 恒成立,则实数
恒成立,则实数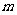 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
7.若直线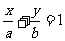 通过点
通过点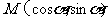 ,则
,则
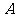 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com