
2.学好本章的关键在哪里?
概率论与其他的数学分支有密切的联系,同时它又具有自己的特点.这主要表现为以下两个方面:一是它与其他数学分支一样具有严格的数学形式;二是它特有的“概率思想”.概率这门学科与现实世界的联系非常密切,它的许多概念和关系都有其现实背景,因此我们常常将概率的结论放在一些现实模型中去思考.在研究概率的过程中,直观常常是理论的先导,为了引进概率论的基本概念和理解它的某些结论,我们必须反复地往返于现实背景和数学理论之间:把某一实际问题归结为概率论的某一模型,用概率的理论加以解释;或是通过现实例子来解释和理解概率论的概念和结论.这是初学者在学习过程中遇到的主要困难,同时也是学好概率的关键.
数理统计是概率论的姊妹学科,和概率论具有相同的现实背景,并且数理统计以概率论为基础.一般来说,概率论是从数学模型出发来推导现实模型的性质,而数理统计则是从观测数据来推测模型的性质,是一种搜集观测数据然后进行分析和推断的数学方法.
[经点答疑]
1.本章应达到的学习目标是什么?
(1)了解随机变量、离散型随机变量、连续型随机变量的概念,会求出某些离散型随机变量的分布列.
(2)了解连续型随机变量的概率密度曲线及概率密度函数的定义、区间概率的几何意义.
(3)了解离散型随机变量的期望和方差的意义,能根据离散型随机变量的分布列求出其期望和方差.
(4)理解简单随机抽样、系统抽样和分层抽样等常用的抽样方法的意义及适用范围,能用上述三种方法从总体中抽取样本.
(5)掌握总体分布的估计方法,即用样本频率分布去估计总体分布.了解累积频率分布的意义,能由样本的频率分布求其累积频率分布.
(6)掌握正态分布和正态总体的概率密度函数的性质,了解生产过程中的质量控制图的原理和使用方法,了解假设检验的基本思想.
(7)会用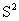 去估计总体方差
去估计总体方差 ,会用S去估计总体标准差
,会用S去估计总体标准差 .
.
9.什么叫样本空间?
当我们掷一枚硬币或一个骰子时,很容易列出所有可能的试验结果.然而,当掷几个骰子时,要列出它的全部可能结果就很麻烦了,并且还有许多试验,它的可能结果是如此之多,以致于我们不可能将所有结果全部列出.因此需要建立一种描述试验结果集合的系统方法.
如图1-16a所示,该图表示我们掷两个骰子的所有可能结果,即集合S,此处S={(x,y)|x和y是整数,1≤x≤6,1≤y≤6}.图1-16b表示:“总数出现四点”这个事件;图1-16c表示:“总数出现七点”这个事件;图1-16d表示:“同时出现四点”这个事件.

上面这种类型的图在研究概率问题时用处很大,在研究概率问题的初期被普遍采用,它在描述试验结果时使用了“点”和“空间”这样的术语,并被沿用至今.一个试验的样本空间是该试验所有结果的一个集合,其中每一个试验结果正好对应这个集合的一个元素.样本点则用来指样本空间中的一个元素.事件指样本空间的子集.
对于掷一个骰子的试验来说,如果D={1,2,3,4,5,6},那么D是一个样本空间,而集合{1,2,3,4,5}就不是样本空间,因为试验结果“6”在集合中没有任何元素与之对应.同样,{1,2,3,4,5,6,7}也不是该试验的样本空间,因为集合中的元素“7”不对应试验中的任何结果.
有时把一些可区别的结果归为一个样本点是有好处的.掷一个骰子的试验可以导出仅由两个样本点“奇数”和“偶数”组成的样本空间.由这两个结果组成的集合是一个样本空间,因为每次掷骰子的结果都正好对应这个集合中的一个元素.注意,这个样本空间的样本点“奇数”把可区别的结果1,3,5并成了一个样本点.我们也能把可区别的结果3和6并成一个样本点“能被3整除的数”.并用{能被3整除的数,不能被3整除的数}作为相应的样本空间.概率理论中允许这样的分组是很重要的.例如,统计学家可能希望处理仅由样本点“高中生”、“初中生”和“小学生”所组成的样本空间,而不是处理他所考察的所有不同的人所组成的样本空间.
开始时,明智的作法是先不将结果分类,而是把每个样本点的可能有的特征表示出来.在掷两个骰子时,即使掷出的点数相同,我们还是设想它们之中一个是红的,一个是绿的,并且以画在图上的36个点为样本空间,不然的话就可能引起误会,误认为“二个一点”和“点数三点”出现的可能性是一样的,或者“总数三点”和“总数七点”出现的可能性是一样的.
在掷一个骰子的试验中,如果取样本空间为{1,2,3,4,5,6},且骰子是均匀的,那么,每个样本点出现的概率是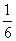 (这样就定义了“均匀”).当我们掷二个骰子时,一个样本空间是笛卡尔积
(这样就定义了“均匀”).当我们掷二个骰子时,一个样本空间是笛卡尔积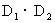 ,这里
,这里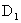 和
和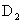 都等于{1,2,3,4,5,6}.正如我们已经看到的,这个样本空间有36个点,分别为{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…,(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}.如果骰子是均匀的,那么每个样本点出现的概率是
都等于{1,2,3,4,5,6}.正如我们已经看到的,这个样本空间有36个点,分别为{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…,(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}.如果骰子是均匀的,那么每个样本点出现的概率是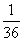 ,当掷三个骰子时,其样本空间是
,当掷三个骰子时,其样本空间是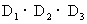 ,这里
,这里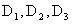 都等于{1,2,3,4,5,6},那么这个样本空间就有6×6×6=216个样本点.如果骰子是均匀的,则每个样本点出现的概率是
都等于{1,2,3,4,5,6},那么这个样本空间就有6×6×6=216个样本点.如果骰子是均匀的,则每个样本点出现的概率是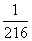 .
.
设E表示事件“两个骰子掷出的点数之和为7”.这样,E={(6,1),(5,2),(4,3),(3,4),(2,5),(1,6)}.如果求“骰子掷出的点数之和为7”的概率是多少这个问题了.它是事件E中所包含的元素的概率之和,即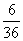 或
或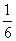 .
.
我们来研究掷三枚硬币的试验.对于这个试验,可以指出两种不同的样本空间,在样本空间{(正正正),(正正反),(正反正),(反正正),(正反反),(反正反),(反反正),(反反反)}中,每个样本点的概率是多少?如果事件E是{(正正反),(正反正),(反正正)},那么事件正的概率是多少?掷三枚硬币,得到两个正面,一个反面(不计顺序)的概率是多少?
对于上述问题,我们的答案是:(1)每个样本点都具有相同的概率;(2)每个样本点的概率为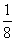 ;(3)事件E的概率是
;(3)事件E的概率是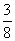 ;(4)得到两个正面,一个反面(不计顺序)的概率为
;(4)得到两个正面,一个反面(不计顺序)的概率为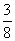 .其中的原因请读者自己思考.
.其中的原因请读者自己思考.
如果说在一个样本空间中,所有样本点都是等可能的,那么就可以确定任何指定事件的概率了.事实上,只要用样本空间的全部样本点数去除属于该事件的样本点数即可.例如,在上面掷三枚硬币的样本空间中,8个样本点看来是等可能的.因此,为了求出两个正面,一个反面的概率,我们要算出属于此事件的样本点数,以及它被样本空间的所有样本点数除所得的商.这样求得的该事件的概率是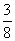 .
.
8.什么叫概率?
概率这个词用来表示在随机现象中某个结果或事件出现的可能性的大小.当一个试验仅能出现有限个确定的结果,且其中的每一个结果出现的可能性都相同时,可以采用概率的古典定义.在某种情况下这也是最简单的一种定义:如果在某一现象可能出现的结果集合中共含有N个元素,那么其中任何一个出现的概率被认为是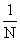 .按照这个定义,抛硬币的试验中被认为出现正面与出现反面的可能性相同,因而出现正面的概率是
.按照这个定义,抛硬币的试验中被认为出现正面与出现反面的可能性相同,因而出现正面的概率是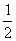 .
.
更一般地,我们可以选定一个由m个可能结果组成的子集(通常称为事件),并来求在一次试验中出现属于此事件的某一结果的概率是多少.一个事件的概率,是出现组成这个事件的可能结果的概率之和.在具有等可能性的场合,这个概率是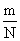 .例如,从含有4张A的54张扑克牌中随机抽取一张,正好抽出A的概率是多少?我们假定在这54张牌中,每一张被抽到的可能性都相同,那么事件“抽中A”由54个等可能结果中的4个组成,因此抽到A的概率是
.例如,从含有4张A的54张扑克牌中随机抽取一张,正好抽出A的概率是多少?我们假定在这54张牌中,每一张被抽到的可能性都相同,那么事件“抽中A”由54个等可能结果中的4个组成,因此抽到A的概率是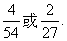
在上面的概率定义的应用过程中有时会遇到一些麻烦.因为有多少种可能的结果,或者怎样才算是等可能的结果不总是显然的.例如,你怎么知道从一组扑克牌中任意抽出一张是等可能的呢?也许洗牌不是很充分,或是某张扑克有点毛病(例如,比其他牌稍大),这就使它更可能被抽到.在掷硬币的试验中,也许出现正面的概率比出现反面的概率稍大一点.事实上,为了使用“等可能”的概念,难免会出现某些争议,在实践中,我们必须通过直观的分析来说明理由.我们从直观上相信,任何一张牌被抽取的可能性相同,硬币的任何一面出现的可能性相等.有时我们的直觉会发生错误,但通常都是有帮助的.概率的古典定义的局限性在于只有假定了所有的结果具有等可能性时,才能应用它.然而概率的语言和思想方法在许多不属于这种类型的场合也应该是适用的.因此我们现在更普遍地来用如下统计概率定义:如果某个试验在相同的条件下重复进行多次,则事件E的概率P是事件E出现的次数与试验次数之商所趋向的那个值.例如,为了确定所抛掷的硬币出现正面向上的概率,我们可尽可能多地抛掷硬币,并记录出现正面向上的次数.如果大约有一半的试验结果是出现正面,我们就断定在抛掷硬币时,出现正面向上的概率是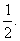
当然,运用上述概念也存在实际的困难.比如多少次才算“多次”呢?在此“多次”中必须出现多少次才能说“约有一半”的试验出现正面呢?假定我们正在研究一个不能重复的现象,那么,根据这个定义,可否研究诸如明天下雨的概率?或下周球赛中A队战胜B队的概率这类问题呢?我们还可以考虑其他的概率定义.比如这个定义:概率是人们对某个特殊事件将会发生的相信程度的一种度量.它称为个人信度定义,采用个人信度定义时,不同的人对同一事件或结果发生的概率的推断有可能不相同,因此这样定义方法并不普遍采用.
采用概率的古典定义和统计定义时,所能得到的概率的最大值是多少?由于事件是试验结果集合的子集,包含在事件中的结果数必小于或者等于可能出现的试验结果数,因此其概率不可能大于1.可能出现的最小概率是多少?假定P是某个试验中某个事件出现的概率,那么,0≤P≤1.
7.为什么要去掉一个最高分和一个最低分?
在我们收看各种体育比赛时,当一个运动员表演完毕后,先由10个(或若干个)评委亮分,裁判长用这10个数据判分时,总要去掉最高分和最低分,再用其余的8个数据的平均值作为该演员的最后得分.现在这已是人们的常识了.
这一常识背后的数学就是数据处理中的代表数问题.
算术平均数是最常用的技巧,在我国也是最普及的数学知识之一.任何一个干部和工人,至少都懂得平均数和百分比这两个概念.“我厂工人平均工资是多少,这次有百分之几的人可以加工资.”这类话人人都能懂.学生的成绩用总分来衡量,也会用总平均来衡量.比较两班学生的某科成绩,也用各班该科得分数的平均数作为衡量标准.至此,人们将平均值奉为至宝,似乎是金科玉律、无可更改的科学定则.
实际上不尽然,用算术平均数来作为代表数,有两个缺点:一是容易受异常值的影响;二是计算比较复杂,不能一眼看出.前面所说的去掉最高分和最低分就是为了避免第一个缺点.让我们看一个极端的例子.如果一个班级有30个学生,其中两个学生逃学旷课,数学考试只得2分和10分.此外,有5个学生得90分,22个得80分,1个得78分.此时该班数学成绩的平均分是:
确实,如以76.67分作为该班平均分,太受那两个得2分和10分的同学牵连了.结果不能反映大多数人的真实状况.从直观上看,应在80分或80分以上才对.于是我们就去掉一个最低分,总平均约是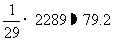 分;如果去掉两个最低分,总平均约是
分;如果去掉两个最低分,总平均约是 分.这似乎比较符合实际了.
分.这似乎比较符合实际了.
但是这种去掉最高分或最低分的方法,在计算全班总成绩时未免有“弄虚作假”之嫌.明明是本班学生,为何不计入总分呢?所以去掉最高分和去掉最低分的方法,不见得都合适.上述的以平均数作为代表数,由于异常值的影响往往不能反映中等水平,一般以为的平均数就是中等水平,乃是误解.上述30个学生的数学成绩中,总平均约是76.67分.某同学得78分,超过平均数,似乎该是“中上”水平了,其实他是倒数第三名!
那么我们用什么办法来刻画“中等水平”呢?这就是数据的中位数.其定义为:设有n个数据,将它们从小到大依次排列为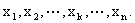 如果n是奇数,则第
如果n是奇数,则第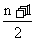 项
项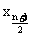 是中位数;若n是偶数,则取第
是中位数;若n是偶数,则取第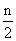 项
项 和第
和第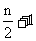 项
项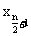 的平均值作为中位数.中位数的特征是比它大的数据个数和比它小的数据个数一样多,它恰在中间位置.
的平均值作为中位数.中位数的特征是比它大的数据个数和比它小的数据个数一样多,它恰在中间位置.
比如,在体操比赛中,规定有四个裁判给一个运动员打分.例如:9.30,9.35,9.45,9.90.其中位数是当中两项的平均值: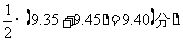
这相当于去掉最低分9.30分和最高分9.90而得出的平均分,体操比赛规定这样给分,就避免了过高分数9.90的影响,同时9.40分处于四个裁判分的中间位数,不偏不倚,十分公正.
在上面的30个学生的数学成绩中,若依大小排列后,第15位和第16位都是80分,所以中位数就是80分.那么78分低于此数,当然是中下水平无疑了.
例如若一个生产小组有15个工人,每人每天生产某零件数目是6,7,7,8,8,8,8,9,10,10,11,12,12,17,18.如以平均数作为标准日产量则是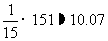 .若取中位数则是第8个数字9.比9大的有7个人,比9小的也有7个人.以9为标准日产量,则有半数人可超产.管理者若希望多数人超产,则应定得较中位数低些;若希望少数人超产,则应定得比中位数大一些.这些都是中位数提供的信息.
.若取中位数则是第8个数字9.比9大的有7个人,比9小的也有7个人.以9为标准日产量,则有半数人可超产.管理者若希望多数人超产,则应定得较中位数低些;若希望少数人超产,则应定得比中位数大一些.这些都是中位数提供的信息.
众数也是常常使用的代表数,即数据中重复出现次数最多的那个数据.例如,全班30人所穿鞋子尺寸为:33号的5人,34号的6人,35号的15人,36号的3人和37号的1人.如取平均数得34.63,此数没多大意义,鞋厂不生产34.63号码的鞋.如取众数,则为35号.该班穿35号鞋的人最多.通常评“最佳”、“最受欢迎”、“最畅销”等往往都和众数有关系.
以上三种代表数各有优缺点,也各有各的用处.各人从不同的角度出发会选取不同的代表数.
比如,美国某厂职工的月工资数统计如下:
月工资数(美元) 得此工资的人数(人)
10000 1(总经理)
8000 2(副总经理)
5000 2(助理)
2000 5
1000 12
900 18
800 23
700 5
500 2
如何来选取该厂的月工资代表数呢?经计算,平均值为1387美元,中位数为900美元,众数为800美元.工厂主为了显示本厂职工的收入高,用少数人的高工资来提高平均数,故采用1387美元.工会领导人则不同意,主张用众数800美元(职工中以拿每月800美元的人最多).而税务官则希望取中位数,以便知道目前的所得税率会对该厂的多数职工有利还是不利,以便寻求对策.
我们常说,“胸中有数”,但是究竟有些什么数,怎样才能有合适的数,确实需要使用一些数据处理的知识才能做到合理、有效和准确.这里所说的代表数仅是其中简单的一例,现代数学的思想就在我们的周围,就在普通的生活中!
6.如何应用期望值?
美好的愿望是人类生存的精神支柱.为一个特定的目标而奋斗,通过艰苦的努力去战胜各种风险,以至终于达到预先的期望,这种成功的喜悦是最激动人心的场面之一:期望!伟大的期望!
期望与风险并存.数学家从期望值来观察风险,分析风险,以便作出正确的决策.古典概率论可以说发源于此.
帕斯卡(Pascal)首先提出了数学期望值的概念.如果卖出彩票1000张,奖金总额为500元,那么帕斯卡会说,你每购买一张彩票的期望值为

如果你买了600张,那么期望值将是
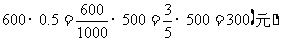
一般地,定义期望值E为概率P乘以奖金数A,即E=P·A.
我们也可以把期望值看成是一长串统计试验的结果.例如上例中,买600张彩票,不妨看做在5000次摸彩中,3000次中奖,2000次落空(概率是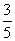 ),奖金为500元,故
),奖金为500元,故
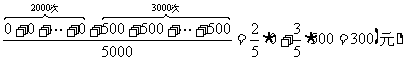
我们可以说,摸奖落空的概率是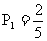 (奖金为
(奖金为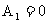 元),获奖的概率是
元),获奖的概率是 (奖金为
(奖金为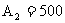 元),所以期望值E可以定义为
元),所以期望值E可以定义为
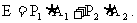
再看一个复杂些的例子.假如有一场竞赛,规则如下:如掷一个骰子,出现1,你赢10元;出现2或3或4,你输2元;出现5或6,不输不赢.这场竞赛对你是否有利?我们还是算期望值.出现1的概率是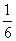 ,出现2,3,4的概率是
,出现2,3,4的概率是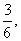 即
即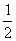 ,出现5,6的概率是
,出现5,6的概率是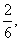 即
即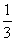 .所以期望值E为
.所以期望值E为
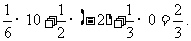
因此,这场竞赛对你是有利的.
以上我们举的是掷骰子、摸彩票的例子,好像如果不去赌博的人永远不会碰到期望值问题,其实不然,我们天天在和期望值打交道.
例如,有一家个体户,有一笔资金,如经营西瓜,风险大但利润高(成功的概率为0.7,获利2000元);如经营工艺品,风险小但获利小(95%会赚,但利润为1000元).究竟该如何决策?于是计算期望值.若经营西瓜,期望值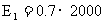 即1400元.而经营工艺品为
即1400元.而经营工艺品为 所以权衡下来,情愿“搏一搏”,去经营西瓜,因它的期望值高.
所以权衡下来,情愿“搏一搏”,去经营西瓜,因它的期望值高.
期望值这个概念,并不是很容易接受的.在有些人看来,如中奖就拿1000元,不中奖就一分钱也没有,这个期望值1元(中将概率0.001乘以1000)是什么“东西”?应该说我国的广大干部和群众对这一数学知识的理解和认识是很差的,远不及“平均数”和“百分比”那样普及.但是在商品经济不断发展的今天,风险处处存在,决策时时要作.如无“期望值”的概念,作为领导者连经济人员写的可行性报告也看不懂,那怎么进行工作?
这里我们不妨举一个某省关于某工程的投资决策的实例.
某新工艺流程如投产成功可收益300万元.但投产之前,必须有小试和中试两步,每次分别需2万元和36万元.小试的成功率为0.7.如做两次小试,则成功率可提高到0.8,小试基础上的中试的成功率为0.7,如直接搞中试的成功率为0.5.于是有三种决策:
(1)一小试一中试,此时工程投资获益的期望值为
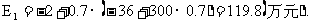
(2)两小试一中试,此时期望值为
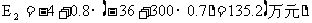
(3)有些领导急于求成,想省去小试,直接搞中试,那么期望值将是
-36+0.5×300=114(万元).
显然,这时采取第二方案最有利.但是,如果一位领导者没有概率知识,对期望值概念一无所知,那么他对这份决策报告也许看不懂,不理解,这就很成问题了.
让我们再举一个用期望值进行决策的例子.
某投资者有10万元,有两种投资方案:一是购买股票,二是存入银行获取利息.买股票的收益取决于经济形势,假设可分三种状态:形势好、形势中等、形势不好(即经济衰退).若形势好可获利40000元,若形势中等可获利10000元,若形势不好要损失20000元.如果是存入银行,假设年利率为8%,即可得利息8000元.又设经济形势好、中、差的概率分别为30%、50%和20%.试问若采用某一标准,应选择哪一种方案?
下面给出采用期望标准的解法.
设 为购买股票,
为购买股票,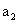 为存银行,
为存银行,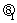 为经济形势好,
为经济形势好,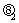 为经济形势中等,
为经济形势中等,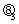 为经济衰退,
为经济衰退,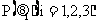 为三种形势的概率,
为三种形势的概率,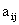 为第
为第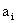 种方案和第
种方案和第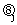 种状态结合的结果,把它们列成一张表(称之为报偿表),即:
种状态结合的结果,把它们列成一张表(称之为报偿表),即:
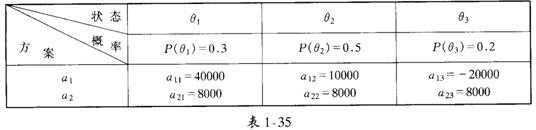
从上表可以看出,如果购买股票在经济形势好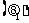 和经济形势中等
和经济形势中等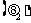 的情况下是合算的,但如果经济形势衰退
的情况下是合算的,但如果经济形势衰退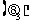 时,则采取存银行的方案比较好.因为这三种状态都有可能出现,采用期望值标准似乎是合理的.所谓期望值标准就是将各种情况下的收益分别乘以其概率之和.根据本例的数字,
时,则采取存银行的方案比较好.因为这三种状态都有可能出现,采用期望值标准似乎是合理的.所谓期望值标准就是将各种情况下的收益分别乘以其概率之和.根据本例的数字, 和
和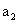 的期望值标准分别为:
的期望值标准分别为:
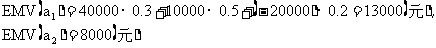
因为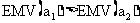 ,所以
,所以 方案期望的收益比
方案期望的收益比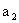 大.按最大收益原则,取期望收益高的方案,淘汰期望收益低的方案,所以应采用购买股票的方案.
大.按最大收益原则,取期望收益高的方案,淘汰期望收益低的方案,所以应采用购买股票的方案.
对上面的结果,有人提出疑问,购买股票方案在经济形势好和经济形势中等时获益自然是高,但若出现经济衰退,岂不损失惨重,他觉得从风险小的角度出发,无论如何也能赚进8000元,似乎存银行方案更优些.下面我们将从机会损失的角度出发,采用最小期望机会损失的标准选择最优方案,看存银行和购买股票两种方案孰优孰劣!这里的机会损失顾名思义就是指采用该方案的实际权益与采取能获得最高收益的方案时收入相比较的差额.
将问题按机会损失列表如下:

两个方案的期望机会损失分别为:
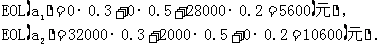
所以按最小期望机会损失的标准,还是应选择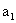 方案.
方案.
说到这里要提另外一个问题:商业情报的价值几何?
大家知道,商场如战场,商业情报可能会挽救一个企业,也可能搞垮一个巨大的集团.于是在现代信息技术高度发达的今天,一些信息咨询公司、市场调查机构就应运而生了.他们手中有某些商品的市场供求情报、市场需求预测,如现在普通市民对VCD的需求如何,DVD大量涌入中国市场的销售前景分析,今年夏天女式服装会流行什么款式等等.如果一个市场预测机构能够对市场经济作出准确的预测,经济的决策者一般是愿意支付咨询费来获取这一信息的.如某时装公司准备明年夏天的上市女装,而一家信息公司经过市场调查对明年夏天女装流行款式有绝对的把握,时装公司是选择盲目生产还是瞄准时机而上呢?显然是后者,如果付一笔小钱就能赚大钱,何乐而不为呢?
这基本上道出了商业情报的价值,说白了就是:我付的咨询费应该小于或等于我能获取的利润.超过了能获取利润的价值的信息是不可取的.那么,从理论上讲,按期望标准,商业情报价值理论上到底是多少呢?以上述10万元钱的投资方案为例,如果知道准确的市场信息,总能选择最优的组合状态,即(40000×0.3+10000×0.5+8000×0.2)-13000=5600(元).
5.抓阄的方法是公正的吗?
概率应用大则可指导生产、科研,小则在日常生活中也大有用处.比如,人们常乐于在分配短缺的情况下用抓阄的办法来解决问题,其合理性保证当然得归功于“概率”.事实上,抓阄的结果是一随机现象,而所谓合理性,无非是说明每个人“中阄”的可能性相等而已!果真如此吗?我们看看下面的问题.
某校校庆,给每个班级5张电影票,初三(2)班是一个团结的集体,共有50个同学,都不愿把电影票占为已有,王老师只好用抽签(抓阄)来决定.他制作了50张小卡片,在其中5张上写上电影票字样,让50个人轮流抽签,抽到的则当仁不让去看电影.但问题是同学们都犹豫了!小华提出了一个问题:“抽签也有先后,第一个人抽到的概率是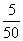 ,如果第一个人抽到,第二个人抽到的概率只有
,如果第一个人抽到,第二个人抽到的概率只有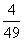 ;如果第一人没有抽到,第二人抽到的概率就是
;如果第一人没有抽到,第二人抽到的概率就是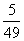 ,抽签未必机会相等!”小陈听到这些话,愣住了,心想:“抽签明明是公平合理的方法,为什么还会有这个奇怪的分析结果呢?”此刻,两人不约而同地把目光转向了王老师,请他解答.
,抽签未必机会相等!”小陈听到这些话,愣住了,心想:“抽签明明是公平合理的方法,为什么还会有这个奇怪的分析结果呢?”此刻,两人不约而同地把目光转向了王老师,请他解答.
王老师指出,小华的分析虽然有道理,但是,他计算出来的两个数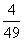 与
与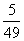 不是第二人抽到的概率,而是在第一人抽到或抽不到的条件下第二人抽到的条件概率.实际上,在抽签时不必争先恐后,先抽与后抽的概率是相等的.这可以用全概率公式计算得知.我们也可以用适当的数学语言来描述这个抓阄试验:“5张电影票,50人抓阄”,其相应的样本空间的样本点可认定是50个阄按抓阄顺序在直线上的一次排列(5个代表有票的阄在这50个位置的某5个位置上).由于事先阄混合得充分均匀,50个阄在直线上的每种排列的可能性是相等的,因而属于古典概型.我们所关心的第k个人抓中有票的阄这一事件可如下构造之:
不是第二人抽到的概率,而是在第一人抽到或抽不到的条件下第二人抽到的条件概率.实际上,在抽签时不必争先恐后,先抽与后抽的概率是相等的.这可以用全概率公式计算得知.我们也可以用适当的数学语言来描述这个抓阄试验:“5张电影票,50人抓阄”,其相应的样本空间的样本点可认定是50个阄按抓阄顺序在直线上的一次排列(5个代表有票的阄在这50个位置的某5个位置上).由于事先阄混合得充分均匀,50个阄在直线上的每种排列的可能性是相等的,因而属于古典概型.我们所关心的第k个人抓中有票的阄这一事件可如下构造之:
设想从5个代表有票的阄中任取一个放在第k个位置上,然后再把剩下的阄安排在剩下的位置上作全排列,如图1-15.
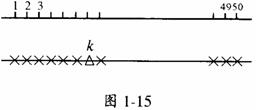
(在第k个位置先安排“有票的阄△”,再安排余下的阄.)从而由乘法原理知,有票的基本事件数为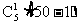 ,以
,以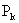 表示第k个人抓中阄的概率,即知
表示第k个人抓中阄的概率,即知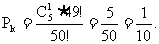 此值不依赖于k,即说明每个人抓中阄的概率都等于
此值不依赖于k,即说明每个人抓中阄的概率都等于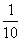 ,而与抓阄顺序无关.从而“试验”结束后的“倒霉”者也就不会怨天尤人了!可见,抽签的方法是公平合理的.
,而与抓阄顺序无关.从而“试验”结束后的“倒霉”者也就不会怨天尤人了!可见,抽签的方法是公平合理的.
这个例子可以推广到n个人抓阄分物的情况.n个阄,其中1个“有”,(n-1)个“无”,n个人排队抓阄,每个人抓到“有”的概率都是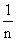 .
.
若n个阄中,有m(m<n)个“有”,(n-m)个“无”,则每个人抓到“有”的概率都是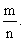
4.小概率事件都可以被忽略吗?
概率论的目的就在于从偶然性中探求必然性,从无序中探求有序.概率论是机遇的数学模型.
你使用过号码锁吗?如果使用过,那你应该知道,一定不能忘了开锁的号码.
比如你家门上的号码锁(如图1-14)有6个拨盘.由于每个拨盘上都有10个数字,因此一共可以组成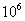 个不同的6位数码,组成每个数码的可能性是相等的,其中只有惟一的一个数码(例如图中的408226)对准开锁线时,锁才能打开.如果你忘记了开锁的号码,想试着拨一个数码就把锁打开,其概率仅有:
个不同的6位数码,组成每个数码的可能性是相等的,其中只有惟一的一个数码(例如图中的408226)对准开锁线时,锁才能打开.如果你忘记了开锁的号码,想试着拨一个数码就把锁打开,其概率仅有: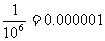 .
.

这个概率是很小的,因此,你想一次就把锁打开几乎是不可能的.
做个有心人,我们会发现,生活中有不少这类发生的可能性很小的事情.我们称这类随机事件为小概率事件.人们从长期的实践中总结出:一件事件如果发生的概率很小的话,那它在一次试验中几乎是不会发生的.数学上称这个结论为小概率原理.
例如,虽然飞机也有发生事故的时候,但据统计,发生事故的概率为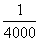 ,可能性很小,因此,人们可以放心地乘坐飞机.
,可能性很小,因此,人们可以放心地乘坐飞机.
又如骗人的摸彩,桌上放有10张外表相同的扑克牌,其中5张“梅花”,5张“方块”,一次让你翻5张牌,如果5张牌同花色(全是“梅花”,或全是“方块”)就算中彩.你很想碰运气,中彩的概率有多大呢?根据组合数公式可知,从10张牌中一次翻5张有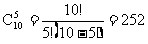 种不同的等可能取法,而翻到5张牌同花色只有两种可能.因此,你中彩的概率为
种不同的等可能取法,而翻到5张牌同花色只有两种可能.因此,你中彩的概率为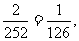 即你如果翻126次,通常才可能中彩一次(还不能保证一定会有一次).这个概率很小,按小概率原理,要想翻一次就中彩几乎是不可能的.
即你如果翻126次,通常才可能中彩一次(还不能保证一定会有一次).这个概率很小,按小概率原理,要想翻一次就中彩几乎是不可能的.
概率小到怎样才算很小呢?这可没有绝对的标准.只有相对于具体要讨论的事情而定,这正像人们说“这老鼠真大”和“这牛太小”一样,我们是让老鼠与老鼠比,牛与牛比.在生产中,比如一批铅笔的废品率为1%,可以认为1%很小而准许出售;但是,若一批注射用的针药有1%不合要求,使用后会危害人的健康,就不能认为1%小了.如果是发射宇宙飞船,100次有一两次失败,则“发射失败”就不是小概率事件了,尽管其概率也不超过0.02.又如,根据某地近数十年来的气象资料,查知发生极大的风暴仅一两次,因而在建造普通平房时,此小概率事件就可以认为是实际上的不可能事件而不予考虑.但在建造高楼大厦时,同一事件就必须加以重视,不能看成小概率事件,因而就不是实际上的不可能事件,不加以重视就会犯错误!
在一般的问题中,一个事件发生的概率低于2%都可以看做是很小的.需要注意,一个小概率事件虽然在一次试验中几乎不会发生,但在多次试验中,常常也会发生.比如在开号码锁的问题中,虽然试开一次几乎不可能把锁打开,但试开很多次时,也有可能把锁打开.
相反地,如果一个事件发生的概率很大(比如在99%以上),那在一次试验中此事几乎一定会发生.
一个小概率事件,不管其概率多么小,其值总是-个确定的正数.设某试验中出现事件A的概率为ε,不管ε>0如何小,如果把此试验不断独立地重复下去,那么A必然会出现1次,从而也必然会出现任意多次.这是因为,第1次试验中A不出现的概率为1-ε,前n次A都不出现的概率为 ,因此,前n次试验中A至少出现1次的概率为
,因此,前n次试验中A至少出现1次的概率为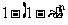 ,当n→∞时此概率趋于1.这表示A迟早出现1次的概率为1.出现A以后,把下次试验当作第1次,重复上述推理,可见A必然再次出现.如此继续,可知A必然出现任意多次,例如,在城市闹区乱放爆竹,就一次而论,引起火灾的可能性并不大,但如果很多人都这样乱放爆竹,则“迟早会引起火灾”这事件发生的可能性就很大.这正是人人皆知的常识在理论上的依据.
,当n→∞时此概率趋于1.这表示A迟早出现1次的概率为1.出现A以后,把下次试验当作第1次,重复上述推理,可见A必然再次出现.如此继续,可知A必然出现任意多次,例如,在城市闹区乱放爆竹,就一次而论,引起火灾的可能性并不大,但如果很多人都这样乱放爆竹,则“迟早会引起火灾”这事件发生的可能性就很大.这正是人人皆知的常识在理论上的依据.
庞加莱说:“最大的机遇莫过于一个伟人的诞生.”之所以如此,一是由于某人的诞生是一系列随机事件的复合:父母、祖父母、外祖父母…的结合,异性的2个生殖细胞的相遇,而这2个细胞又必须含有某些产生天才的因素;二是婴儿出生以后,各种偶然遭遇在整体上必须有利于他的成功,他所处的时代,他所接受的教育,他的各项活动,他所接触的人、事与物,都需为他提供好的机会.所以,某个特定的人要成为伟人,可能性是极小的.不过,尽管如此,各个时代仍然伟人辈出.一个人成功的概率虽极小,但几十亿人中总有佼佼者,这就是所谓“必然寓于偶然之中”的一种含义.应用小概率原理于伟人问题,一个人成为伟人的概率固然非常小,但千百万人中至少有一个伟人就几乎是必然的了.
“必然寓于偶然之中”的另一含义是大数定律,它的特殊情形是频率的稳定性,即频率趋于概率.设某试验中事件A出现的概率为p>0,将此试验独立地重复n次,其中A出现了m次,于是频率为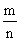 .根据大数定律,当n→∞时,必然有
.根据大数定律,当n→∞时,必然有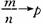 .因此,当n充分大时,得m≈np.
.因此,当n充分大时,得m≈np.
我们不能确切预知一个婴儿的性别,只知他是男性的概率为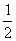 .但由于上述定律,我们可以断言,100万婴儿中,约有
.但由于上述定律,我们可以断言,100万婴儿中,约有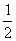 即50万个男婴,这几乎是必然的.
即50万个男婴,这几乎是必然的.
3.“同年同月同日生”真的很稀奇吗?
如果你学过概率,你就能得出一些使人吃惊的结论来,让我们来看一个著名的数学问题:生日的相合,367个人中间,肯定有两个人的生日相同.[注:这里我们只讨论出生的月份及日期,而不考虑年份.]这是根据抽屉原理得来的(因为一年最多只能有366天).抽屉原理可叙述为:假如有n+1个(或更多)物体装入n个盒子,那么一定有某个盒子至少装有两个物体.
生日问题也许令人困惑:23个人中有两人生日相同的概率便超过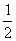 .你也许认为这是巧合.其实,这个奥妙也可以用概率的方法推断出来.为了简单,我们不记闰年,一年按365天算.
.你也许认为这是巧合.其实,这个奥妙也可以用概率的方法推断出来.为了简单,我们不记闰年,一年按365天算.
某年级有n个人(n≤365),问至少有两个人的生日在同一天的概率有多大?
试验是对人数为n的年级进行生日调查,试验的基本结果是n个人生日的一种具体分布.由于生日出现的随机性,保证了n个生日种种分布的等可能性.
基本事件的数学结构--构造性处理:把365天设想为365个“房间”,然后按n个人的生日“对号人室”.这相当于n个可辨质点的每一个都以相同的概率,等可能地被分配到某一“室”内.形象示意图如下:
×表示人 □表示日子
|
|
× |
×× |
|
|
|
|
××× |
|
… |
×× |
× |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
364 |
365 |
图1-13
基本结果总数就是把n个人安排进这365个“房间”的所有可能的不同方法数.基本结果的差异不仅依“人”、依“房”,而且还依“房”内的“人数”相鉴别.因而基本事件总数恰为从365个不同元素中每次取出n个的允许重复的排列数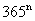 (乘法原理).
(乘法原理).
所关心的事件A={至少有两人的生日在同一天}={有两个人的生日在同一天}U{有三个人的生日在同一天}U…U{n个人的生日在同一天}.这是一个比较复杂的事件,我们应从反面去考虑原事件的逆事件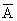 的结构:
的结构:
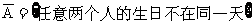
={n个人的生日全不相同}
={365个不同元素,每次任取n个依一定的顺序排成一列}.
这样就抓住了事件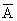 的数学结构的本质,从而可知
的数学结构的本质,从而可知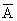 的基本事件数为
的基本事件数为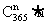 !.由互逆事件的概率关系,即知
!.由互逆事件的概率关系,即知

具体地计算可有下面的结果:
n人中有两个生日相同的概率
|
n |
15 |
20 |
23 |
24 |
25 |
30 |
40 |
50 |
55 |
|
P |
0.25 |
0.41 |
0.51 |
0.54 |
0.57 |
0.71 |
0.89 |
0.97 |
0.99 |
表1-34
从表1-34中可知,只要人数n≥55,则有2人生日相同的概率已相当接近1了.
不少团体人数都在23人以上,若有2人生日相同,可能彼此觉得真有缘分,备感亲切.而我们现在知道这其实是一件很容易发生的事件.
中国人有十二种属相,这由某人生于何年而定.可能会令你不解的是:任意四个人中,有两人属相一样的可能约有一半.而在一个6口之家中,几乎可以断定有两个人属相一样.这种问题也是概率论研究的对象.
有人曾查阅资料发现:美国前36任总统中有两个人生日一样,3人死在同一天(当然年份不同).
概率论这个数学工具是和人们“朝夕相处”的.
2.“街头摸奖”可信吗?
你相信那些用摸彩来吸引人去碰“运气”的游戏吗?我们不妨来试试下面的彩球游戏.准备一个布袋,内装6个红球与6个白球,除颜色不同外,六个球完全一样,每次从袋中摸6个球,输赢的规则为:
6个全红 赢得100元
5红1白 赢得50元
4红2白 赢得20元
3红3白 输100元
2红4白 赢得20元
1红5白 赢得50元
6个全白 赢得100元
如果你摸出了3红3白则输100元.而对于其他六种情况,你均能赢利相应的钱数,而不用花其他的钱,怎么样?动心了吗?[注:这个规则有时称为“袋子”模型]
乍一看,此规则似乎处处对顾客有利,许多人都难免动心去碰碰“运气”,甚至有人连连试了数次.然而,顾客一个个都免不了扫兴而去,一连十几个人各试了5次,结果都以失败告终,每人输的钱在60元到130元不等,而且试的次数越多,则输的越多.
其实,我们想一想也该明白,天下哪有免费的午餐呢?但要知道为什么会输就要用到我们的概率的知识了,要弄清这个问题并不难,我们不妨逐一计算顾客中奖的可能性,也就是输赢规则中7种情况各自出现的概率大小.
用概率论的语言说,假如7种情况是等可能的,则赢的机会为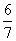 ,输的机会仅为
,输的机会仅为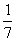 ,摸7次有6次都应该赢.但游戏的妙处就在于这7种情况的发生不是等可能的.由于球的形状、大小、重量等完全一样,所以我们无法看到的情况下是无法区分红球和白球的,任意摸6个球,不论红或白,共有
,摸7次有6次都应该赢.但游戏的妙处就在于这7种情况的发生不是等可能的.由于球的形状、大小、重量等完全一样,所以我们无法看到的情况下是无法区分红球和白球的,任意摸6个球,不论红或白,共有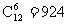 种可能,由此就可以计算出摸到5红1白的概率为
种可能,由此就可以计算出摸到5红1白的概率为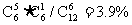 .而摸到3红3白的概率为
.而摸到3红3白的概率为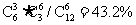 .可见,输钱的可能性约占
.可见,输钱的可能性约占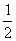 ,正是由于各种情况出现的概率不均等,才导致了人们上当受骗,这7种情况出现的概率如下所示:
,正是由于各种情况出现的概率不均等,才导致了人们上当受骗,这7种情况出现的概率如下所示:
结果 出现的概率
6个全红 0.1%
5红1白 3.9%
4红2白 24.4%
3红3白 43.2%
2红4白 24.4%
1红5白 3.9%
6个全白 0.1%
很显然,上面7种情况的概率加起来是1,它们把全部的可能性100%进行了不均等的概率分配,从中还可以看出,要想摸出“6个全红”或“6个全白”的可能性仅为0.1%,相当于1000次中只有1次会赢100元,这是一个概率很小的事件,根据实际推断原理,在一次摸取中,基本上是不会发生的,而摸到3红3白的可能性为43.2%,即几乎每两次就有一次可能出现,几乎有一半的机会输掉100元,这就是摸得越多,输得越多的原因.为了进一步分析,我们设随机变量η表示赢的钱数,则η的分布列应为
|
η |
100 |
50 |
20 |
-100 |
|
P |
0.002 |
0.078 |
0.488 |
0.432 |
表1-33
所以,我们赢钱的数学期望为

=2×(0.1+1.95+4.88)-43.2
=-29.34.
由期望的实际意义可知,我们每摸一次,平均就输掉29.34元.
事实上,这种摸彩是一种“机会游戏”,它不过是概率论这门学科的低极表现形式而已,并不是什么新鲜的玩意儿,但若涉及到金钱,它就变成了赌搏.这就告诉我们,遇到诱惑时要谨慎行事,一般来说,诱惑越大的游戏,就越能使人输钱,以至于倾家荡产.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com