
8.如果ξ服从0-1分布,又知ξ取1的概率为它取0的概率的两倍,写出它的分布列和分布函数.
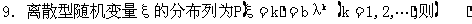
A.b>0 B.λ>0

7.用随机变量来描述掷一枚硬币的试验结果,写出它的概率分布(概率函数)和分布函数.
6.同时掷三个骰子,观察它们出现的点数,求三个骰子出现的最大点数X的分布列.
5.口袋里装有5个白球和3个黑球,任意取一个,如果是黑球则不放回,而另外放入一个白球,这样继续下去,直到取出的球是白球为止,求直至取到白球所需的抽取次数X的概率分布.
4.某种零件共12个,其中9个正品,3个次品.从中抽取一件,遇次品不再放回,继续取一件.直至取出正品为止.求在取出正品以前已取出次品数的概率分布.
3.对某一目标进行射击,直至击中为止,如果每次射击命中率为p,求射击次数的概率分布.
2.六张卡片上,分别写有号码1,2,3,4,5,6.从中随机地同时取其中三张,设随机变量X表示取出的三张卡片上的最大号码,求X的分布列.
1.设在15个同类型的零件中有2个是次品,在其中取3次,每次任取1个,作不放回抽样,以X表示取出次品的个数.
(1)求X的分布列.
(2)画出分布列的图形.
8.如何作到真正的随机抽取?
在简单随机抽样的过程中,我们采用了随机抽取的办法.所谓的随机抽取就是要求在抽样过程中各个个体被抽到的概率都相等.但是,如何保证我们的抽取过程是真正随机的呢?
在本书中,我们不能随便地使用“随机”这个词,读者可能已经猜到了“随机”这个词是什么意思.然而仔细研究这个问题以后,就会清楚地知道“随机性”不总是容易得到的,并且它实际上也不可能被验证.
例如,有这样一个问题,我们想从一群人中选择一个人,检查他有无癌症.假定要你从1000人中随机选出一个人,你怎么选法呢?要知道,如果选取是真正随机的,每一个人被选中的概率必须相等.
你可以采用的一种方法是:把每个人的名字(假定1000人中没有重名的)写在一张小纸片上,然后把所有的纸片放在一个大容器中搅抖均匀.让一个蒙住眼睛的小姑娘(她肯定是不作弊的)从中抽取一张.这个办法最明显的问题是搅拌均匀的问题.果真能把1000张写有名字的小纸片搅拌均匀吗?有大量证据说明,搅拌均匀的困难远比一般所想像到的要大得多.
另一种办法是做一个旋子,它上面有一个可以旋转的箭头,箭头的一端能在10个数字中的任何一个数字上停下来.然后将这1000个人从000到999编上号.转动旋子3次所得到的三位数字表明选中了哪个人.例如,旋转结果的顺序是3,2,3.则选中了编号为323的那个人.我们用的旋子如图1-3所示.
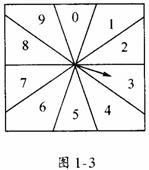
如果下一个被选中的人是333号.你可以怀疑这个旋子不正吗?旋子是否在3这个位置上被什么东西卡住了呢?(某些街头猜奖的小贩会在特定的数字下放一块磁铁来吸引指针指向这个数字)是这样的,如果旋子没有缺陷,333应该和其他数字出现的可能性相同.显然,这种办法的主要困难在于做一个完好无缺的旋子.
还有哪些别的办法,能“公平地”或真正随机地从1000个人中选出一个人来呢?我们知道,现在利用计算机运行一种“随机数发生器”的程序就可以产生随机数.但如果你有一定的编程知识的话就会知道,任何“随机数发生器”都依靠-个“种子”值来产生-系列“随机的”数字,我们通常称之为“伪随机数”.计算机作为一种有限状态的机器,是不可能产生真正随机的数字序列的.
在学过统计学的科学家中,现在通用的办法是使用随机数表.(如课本附录中所列)随机数表是这样一个数字列,使每一个数字在任何一个位置出现的可能性都相同,即都是 .随机数表在实际的构造中是非常困难的,需要有专门的技术并进行大量的工作.下面所列就是
.随机数表在实际的构造中是非常困难的,需要有专门的技术并进行大量的工作.下面所列就是
一张简单的随机数表.
列
|
行 |
|
|
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
|
||
|
1 |
|
9 |
5 |
8 |
3 |
2 |
|
7 |
6 |
1 |
4 |
5 |
|
|||
|
2 |
9 |
9 |
8 |
1 |
3 |
4 |
4 |
6 |
3 |
1 |
||||||
|
3 |
7 |
7 |
2 |
1 |
0 |
3 |
1 |
1 |
4 |
8 |
||||||
|
4 |
1 |
3 |
2 |
6 |
8 |
0 |
2 |
6 |
0 |
9 |
|
|||||
|
5 |
4 |
4 |
2 |
8 |
5 |
7 |
1 |
7 |
3 |
5 |
||||||
|
6 |
7 |
0 |
5 |
2 |
6 |
4 |
5 |
9 |
5 |
3 |
||||||
|
7 |
8 |
8 |
3 |
8 |
6 |
1 |
1 |
2 |
2 |
2 |
||||||
|
8 |
8 |
3 |
1 |
6 |
1 |
7 |
3 |
9 |
9 |
4 |
||||||
|
9 |
5 |
0 |
2 |
1 |
4 |
7 |
1 |
7 |
2 |
1 |
|
|||||
|
10 |
9 |
7 |
6 |
8 |
9 |
2 |
9 |
3 |
4 |
1 |
||||||
表1-20
我们利用上表来从1000个人中选择一个人,继续采用上面对人的编号,于是采用表中第-行第1,2,3列上的数字,我们就随机地抽出一个编号为958的人.如果我们要选择一个四人委员会,那么第二人该是327号,第三人是614号,第四人是599号.在这个抽取三位数的过程中,如果某个三位数第二次出现,就略去这个数字,而往下再取一个三位数,因为一个人不能担任四人委员会的两个成员.如果不是选择四人委员会,而是发放四份奖金.并且允许-个人拿到两份或多份奖金,那么就不能略去第二次出现的那个三位数,而是应该把两份奖金发给以它为编号的那个人.
假定我们要在本季度的首轮球赛中将八个球队分成四组.将八个球队从1到8编上号,从随机数表的第二行第三列开始(从表中第一个例子结束的地方开始),把8队和1队分成一组,3队和4队分成一组,(跳过第7列的数字4,因为不能把4队分到两个组中),6队和7队分成一组,最后2队和5队分成一组.当然,前三组分好后,最后-组也就确定出来了.如果在表中出现了数字0或9,就直接跳过它,因为0和9不是球队的编号.
还可以用随机数表决定某个球队是主队还是客队,考虑这个球队过去的成绩就可以做到这一点.
假定在上一赛季中8队赢了15场,1队赢了5场.我们希望在第-场比赛中1队成为主队的机会大于8队,并希望这个机会与它们过去的成绩有关,我们用数字00到14表示1队成为主队,数字15到19表示1队成为客队.在随机数表中上例结束处开始,即从第3行第2列开始,得到数字72,因为72是一个与本问题无关的数字,舍弃它.再查下两个数字,得到10,于是1队在第一场比赛中应为主队.
上面讨论了随机数表在随机抽取中的一些应用.使用随机数表应该从左到右读完-行后再读下一行,行间的空隙只是为了便于看清表中数字的位置.另外,从哪一个位置开始读取表中的数字,有时是有一些窍门的,如果正规地使用这个表,应该从头开始,用完之后做下记号,下-次再接着往下用.但是如果试验者用完这个表后注意到下面几个数字,而在下一次试验中又将它回忆起来,那就有可能破坏试验的客观性.同样,在全班都使用随机数表再将结果合并起来时,如果班上所有同学都从表中同一处开始,那么合并的结果就不是随机的了.正确的方法是各人开始于不同的地方,而各人选择起始点时应该采用随机数表进行随机选取.
让我们看一下下面的例题.
例 下表表示上一赛季10个篮球队获胜的场数,利用随机数表将这些队在下一赛季的第一轮比赛进行分组,在每一组中指定一个队为“主队”或“客队”,使得成绩较差的队比战绩较好的队成为主队的可能性比较大,叙述你所采用的分组及指定“主队”和“客队”的方法.比赛结果见下表.
|
球队 |
上一赛季获胜的场数 |
|
A B C D E F G H I J |
8 15 19 7 4 5 19 20 3 0 |
表1-21
思路启迪 先将10个球队A、B、C、D、E、F、G、H、I、J从0到9编号.即A队编为0号,B队编为1号,C队编为2号,依此类推,J队被编为第9号.利用上面提供的随机数
表,对这10个球队进行分组.从表的第一行第一列开始,得到5个数对,分别为:9和5;8和3;2和7;6和1;4和5;在上述五个数对中,将对应的数字换成表示球队的字母就得到了一种对10个球队随机分组的方法,即J队和F队为一组,I队和D队为一组,C队和H队分为一组,G队和B队分为一组,剩下的E队和A队分成一组,注意最后一组数中重复出现了数字5,我们将其直接去掉,又因为前4组已分好,故这样做不会影响我们对各组的划分.
在每组中指定主队和客队的方法为:以第一组J队和F队为例,因为F队在上一赛季赢了5场而J队则一场也没赢,故我们希望J队获得主场的机会比F队获得主场的机会大.我们用数字0到4表示“J队成为主队”,那么从随机数表的第2行开始,前三个数字9,9,8不在0到4之间,我们跳过这三个数字,第四个数字为1,在0到4之间,故让J队成为主队.再以第2组即I队和D队这一组为例:因为I队在第一赛季中赢了3场而D队在第一赛季中赢了7场,故划分时用数字0到数字6代表“1队成为主队”,而以数字7到数字9代表“D队成为主队”.从随机数表的第2行第5列(即上面用到的数字1后的数字)开始选数字,选到的数字为3.在0到6之间,故令I队成为主队.其他组的主队与客队的划分方法类似,请读者自行决定.
规范解法 略.
7.离散型随机变量的期望和方差是如何计算的?
离散型随机变量的数学期望和方差的计算主要有以下三种方法.
方法一:用定义求出.
先来回顾一下期望和方差的定义:设η为离散型随机变量,其分布列为:
 |
 |
 |
 |
 |
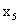 |
… |
 |
… |
|
P |
 |
 |
 |
 |
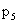 |
… |
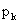 |
… |
表1-16
若和式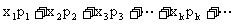 可以计算,则称之为随机变量η的数学期望,记作
可以计算,则称之为随机变量η的数学期望,记作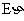 ,即
,即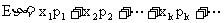 [注:我们一般见到的分布列都为有限项,所以其期望值都是可以计算的.对于无限项的分布列,在计算时要用到级数和极限的内容,我们这里暂不作介绍.]
[注:我们一般见到的分布列都为有限项,所以其期望值都是可以计算的.对于无限项的分布列,在计算时要用到级数和极限的内容,我们这里暂不作介绍.]
若随机变量η的数学期望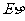 存在,且
存在,且 也存在(这里的
也存在(这里的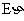 是一个常数),则称
是一个常数),则称 为η的方差,记为
为η的方差,记为 .即
.即 ,显然
,显然 .根据上述期望的定义可得方差的计算公式为:
.根据上述期望的定义可得方差的计算公式为: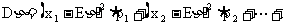
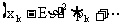 ,计算随机变量的方差除用上述定义之外,最常用的是下面的简化公式:
,计算随机变量的方差除用上述定义之外,最常用的是下面的简化公式:
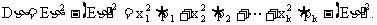
来看下面的例题:
例1 有3只球和4只盒子,盒子的编号为1,2,3,4.将球逐个独立地、随机地放入四个盒子中去.以η表示其中至少有-只球的盒子的最小号码(例如事件{η=3}表示第1号,第2号盒子都是空的,第3号盒子中至少有-只球),试求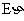 .
.
思路启迪 因为用公式计算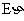 时必须知道随机变量η的分布列.所以该题的第一步是计算η的分布列.由题述,显然η的可能取值为1,2,3,4.再来看η取各值的概率.当η=1时,表示第1号盒子中至少有一只球,其球的放法共有
时必须知道随机变量η的分布列.所以该题的第一步是计算η的分布列.由题述,显然η的可能取值为1,2,3,4.再来看η取各值的概率.当η=1时,表示第1号盒子中至少有一只球,其球的放法共有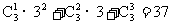 种,这是因为第l号盒子仅有一只球的放法为
种,这是因为第l号盒子仅有一只球的放法为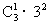 种,有两只球的放法共有
种,有两只球的放法共有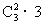 种,有3只球的放法共有
种,有3只球的放法共有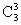 种.
种.
当η=2时,表明1号盒子为空,第2号盒子至少有一个球.其球的放法总数有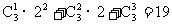 种.这是因为第2号盒子只有一只球的放法有
种.这是因为第2号盒子只有一只球的放法有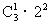 种,有两只球的放法有
种,有两只球的放法有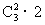 种,有三只球的放法共有
种,有三只球的放法共有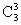 种.
种.
当η=3时,表示第1号,第2号盒子均为空,第3号盒子中至少有一只球,其球的放法有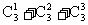 =7种,这是因为第3只盒子只有一只球、两只球、三只球的放法分别为:
=7种,这是因为第3只盒子只有一只球、两只球、三只球的放法分别为: 种.
种.
当η=4时,表明第1、2、3号盒子都为空,第4号盒子定有3个球,球的放法只有一种.
而3只球,放入4只盒子,盒子装球的个数不限,共有 种放法,所以
种放法,所以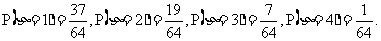
规范解法 由上面分析可得η的分布列为
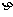 |
1 |
2 |
3 |
4 |
|
P |
37/64 |
19/64 |
7/64 |
1/64 |
表1-17
因此,按照期望的计算公式可得:
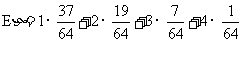
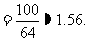
例2 从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,且概率都是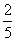 .设随机变量η表示途中遇到红灯的次数,求η的分布列和数学期望.
.设随机变量η表示途中遇到红灯的次数,求η的分布列和数学期望.
思路启迪 因为在每个交通岗只会发生两件事“遇到红灯”与“不遇到红灯”,且两事件相互矛盾,因此遇到红灯的次数η是一随机变量且服从二项分布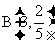 .
.
规范解法 随机变量η服从二项分布,即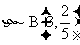 ,η的可能取值为0,1,2,3,易求得:
,η的可能取值为0,1,2,3,易求得:

于是所求的分布列为:
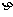 |
0 |
1 |
2 |
3 |
|
P |
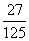 |
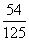 |
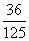 |
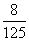 |
表1-18
η的数学期望为
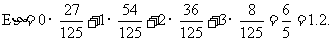
方法二:利用常见离散型随机变量的数字特征公式求之.
为了方便应用,下面将几种常见离散型随机变量的期望和方差列成表,以备查用.希望读者熟记表中所列的期望和方差的计算公式.
|
分布名称 |
分布列 |
期望 |
方差 |
|
0-1分布 |
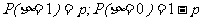 |
P |
P·(1-P) |
|
二项分布 |
 |
n·p |
np·(1-p) |
|
几何分布 |
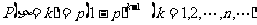 |
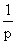 |
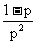 |
表1-19
[注:计算期望和方差时,应先考查其分布是否是常见分布.属常见分布,其方差与期望可直接利用公式求之.不必像例1那样先求分布列,再用定义计算,那样太麻烦,且容易算错.]
例3 某人掷不均匀钱币,出现反面的概率为P,(0<P<1),求在两次出现反面之间出现正面的次数的概率分布和数学期望.
思路启迪 设随机变量η表示两次出现反面之间出现正面的次数,则η的一切可能值为一切非负整数,即0,1,2,…,n,….设出现m次正面后出现反面,则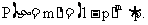
规范解法 设η表示两次出现反面之间出现正面的次数,则η服从几何分布,参数为P,由上表可知η的率分布为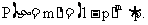 其数学期望为
其数学期望为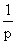 .
.
例4 设一次试验成功的概率为p,进行100次独立重复试验.当P=( )时,成功次数的标准差的值最大,其最大值为( ).
思路启迪 设100次独立重复试验中的成功次数为随机变量η.所以η服从二项分布,即η-B(100,P),根据上表中所列公式可得随机变量η的方差为:
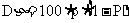 .
.
规范解法 设随机变量η表示100次试验中成功的次数,很明显η-B(100,P),所以η的标准差为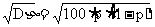 因
因

显然当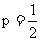 时,100p·(1-p)达到最大,即
时,100p·(1-p)达到最大,即 的值最大.其最大值为
的值最大.其最大值为
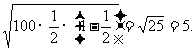
[注:常将p(1-p)配成完全平方式: 来讨论服从二项分布的随机变量其方差的大小问题.]
来讨论服从二项分布的随机变量其方差的大小问题.]
方法三:随机变量分解法.
将随机变量η分解成若干个随机变量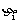 之和,把求Eη转化为
之和,把求Eη转化为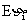 :
:
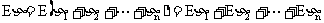
若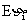 易于求出,则Eη的计算就非常简便,这种处理方法称为随机变量分解法.
易于求出,则Eη的计算就非常简便,这种处理方法称为随机变量分解法.
例5 设随机变量η-B(n,p)试求Eη和Dη.
思路启迪 因为η-B(n,p)设

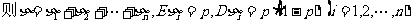
规范解法
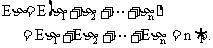

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com