22．掷20个骰子，求这20个骰子出现的点数之和的数学期望．

21．已知随机变量X服从二项分布B(n，p)，证明：EX＝np,DX＝npq (q＝1－p)．

20．设盒中放有五个球，其中两个白球，三个黑球．现在从盒中一次抽取三个球，记随机变量X、Y分别表示取到的三个球中的白球数与黑球数，试计算EX，DX；EY，DY．

18．假定有n＝5个工人独立地工作，假定每个工人在一小时内平均有12分钟需要电力．

(1)求在同一时刻有3个工人需要电力的概率．

(2)如果最多只能供应3个人需要的电力，求超过负荷的概率．

17．已知n只电容器中有一只已被击穿，为把这只被击穿了的电容器挑出，我们逐只作检验，以ξ表示需作检验的次数，求ξ的概率分布．

16．设ξ的概率分布为求C值及概率P(ξ＝3)，

P(ξ<3)，P{(ξ＝2)∪(ξ＝3)}．

14．将一枚硬币扔三次，设ξ为三次中出现正面的次数，求P(ξ＝k)，k＝0，1，2，3，P(ξ≤1)，P(0<ξ<3)．

13．随机变量X的概率密度函数如图1-17所示

(1)求其概率密度函数f(x)．

(2)求其分布函数F(x)．

(3)求X落在[0.2，1.2]内的概率．

12．设随机变量X的所有可能值为1，2，…，n，且已知概率P(X＝k)与k成正比，即P(X＝k)＝a·k (k＝1，2，…，n)．求常数a的值．

10．已知离散型随机变量X只取－1，0，1，四个值，相应概率为1/(2C)，3/(4C)，5/(8C)，7/(16C)，计算概率P(|X|≤1|≥0)．

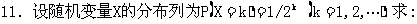
(1)P(X＝偶数)．

(2)P(X≥5)．

(3)P(X＝3的倍数)．