
19. (本小题满分13分)
已知动圆过定点 ,且与定直线
,且与定直线 相切.
相切.
(1)求动圆圆心的轨迹C的方程;
(2)若 、
、 是轨迹C上的两不同动点,且
是轨迹C上的两不同动点,且 .
分别以
.
分别以 、
、 为切点作轨迹C的切线,设其交点Q,证明
为切点作轨迹C的切线,设其交点Q,证明 为定值.
为定值.
18.(本小题满分12分)
某篮球职业联赛的总决赛在甲队与乙队间角逐,采用五局三胜制,即若一队先胜三场,则此队获胜,比赛结束,雅创教育网因两队实力相当,每场比赛获胜的可能性相等,据以往资料统计,第一场比赛组织者可获门票收入30万元,以后每场比赛门票收入都比上一场增加10万元,问:
⑴组织者在此次总决赛中获得门票收入不少于180万元的概率是多少?
⑵用 表示组织者在此次总决赛中的门票收入,求
表示组织者在此次总决赛中的门票收入,求 的数学期望?
的数学期望?
17.(本小题满分12分)
设集合 .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
16.(本小题满分12分)在 ,已知
,已知 ,求角A,B,C的大小。
,求角A,B,C的大小。
15、在 上的可导函数
上的可导函数 ,当
,当 时取得极大值,当
时取得极大值,当 时取得极小值,则
时取得极小值,则 的范围是___________
的范围是___________
14. 已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为
 且
且 ,则
,则 的最小值是
.
的最小值是
.
13. 已知实数 满足
满足 ,则
,则 的最小值是 .
的最小值是 .
12.已知函数 的图象恒过定点A. 若点A在直线mx+ny+1=0上,其中mn>0,当
的图象恒过定点A. 若点A在直线mx+ny+1=0上,其中mn>0,当 有最小值时,椭圆
有最小值时,椭圆 的离心率为
。
的离心率为
。
11. 设向量 ,若向量
,若向量 与向量
与向量 共线,
共线,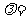 .
.
10. 设 R,
R, 是函数
是函数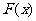 的单调递增区间,将
的单调递增区间,将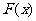 的图象按向量
的图象按向量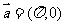 平移得到一个新的函数
平移得到一个新的函数 的图象,则
的图象,则 的一个单调递减区间是
的一个单调递减区间是
A. B.
B. C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com