
1.(2009上海八校联考) 是无穷数列,已知
是无穷数列,已知 是二项式
是二项式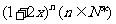 的展开式各项系数的和,记
的展开式各项系数的和,记 ,则
,则 _______________。
_______________。
答案 
19、(2009上海普陀区)设数列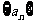 的前
的前 项和为
项和为 ,
, . 对任意
. 对任意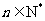 ,向量
,向量 、
、 都满足
都满足 ,求
,求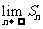 .
.
解 因为 ,所以由条件可得
,所以由条件可得 ,
,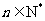 .
.
即数列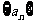 是公比
是公比 的等比数列.
的等比数列.
又 ,所以,
,所以, .
.
9月份更新
18、(2009冠龙高级中学3月月考)由函数 确定数列
确定数列 ,
, ,函数
,函数 的反函数
的反函数 能确定数列
能确定数列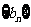 ,
, ,若对于任意
,若对于任意 ,都有
,都有 ,则称数列
,则称数列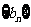 是数列
是数列 的“自反数列”。
的“自反数列”。
(1)若函数 确定数列
确定数列 的自反数列为
的自反数列为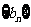 ,求
,求 的通项公式;
的通项公式;
(2)在(1)条件下,记 为正数数列
为正数数列 的调和平均数,若
的调和平均数,若 ,
,
 为数列
为数列 的前
的前 项和,
项和, 为数列
为数列 的调和平均数,求
的调和平均数,求 ;
;
(3)已知正数数列 的前
的前 项之和
项之和 。求
。求 的表达式。
的表达式。
解 (1) 由题意的:f –1(x)= = f(x)=
= f(x)= ,所以p = –1,所以an=
,所以p = –1,所以an=
(2) an= ,dn=
,dn= =n,
=n,
Sn为数列{dn}的前n项和,Sn= ,又Hn为数列{Sn}的调和平均数,
,又Hn为数列{Sn}的调和平均数,
Hn= =
= =
=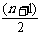
 =
= =
=
(3) 因为正数数列{cn}的前n项之和Tn= (cn+
(cn+ ),
),
所以c1= (c1+
(c1+ ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
当n≥2时,cn = Tn–Tn–1,所以2Tn = Tn–Tn–1
+ ,
,
Tn +Tn–1 =  ,即:
,即: = n,
= n,
所以, = n–1,
= n–1, = n–2,……,
= n–2,……, =2,累加得:
=2,累加得:
 =2+3+4+……+ n,
=2+3+4+……+ n,  =1+2+3+4+……+ n =
=1+2+3+4+……+ n = ,Tn=
,Tn=
17、(2009宣威六中第一次月考) = .
= .
答案 -3
16、(2009上海九校联考)设常数 >0,
>0,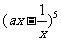 的展开式中,
的展开式中, 的系数为
的系数为 ,
,
则
答案 
15、 (2009上海闸北区)若
(2009上海闸北区)若 展开式的第9项的值为12,则
展开式的第9项的值为12,则
 = .
= .
答案 2
14、(2009张家界市11月考)已知 ,则
,则 =
(其中
=
(其中 为
为
虚数单位)
答案 1-i.

13. (湖北省2009年3月高三八校第二次联考理科) 设 是
是 的展开式中
的展开式中 项的系
项的系
数( 、
、 、
、 、…),则
、…),则 ________.
________.
答案 18
12、(2009厦门一中)若函数 在
在 处的
处的 ,则
,则 等于_______________
等于_______________
答案 -2
11. (北京市丰台区2009年3月高三统一检测理) 设等比数列 的前
的前 项和为
项和为 ,若
,若
 ,则
,则 = 。
= 。
答案 4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com