
16、解:(1)因为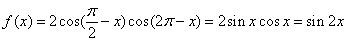 ………4分
………4分
所以函数 的最小正周期为
的最小正周期为 .……………………………………………6分
.……………………………………………6分
(2)因为 ……………8分
……………8分
由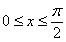 ,得
,得 ,从而
,从而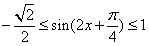 ……………10分
……………10分
所以当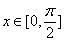 时,
时,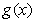 的最大值为
的最大值为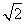 ,最小值为-1.………………12分
,最小值为-1.………………12分
(17)(本小题共12分)
解答:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE 平面CDB1,AC1
平面CDB1,AC1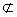 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
18(本题满分12分)、
解:(1)∵函数 的图象经过点
的图象经过点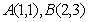 ,则
,则
 ,解得
,解得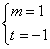 ,∴
,∴ ,得
,得
则
(2)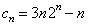 ,
,
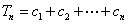 =
=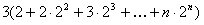

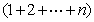
令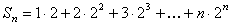 …①
…①
 …②
…②
①- ②: 
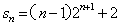

15、 1
13、 14、
14、
11、2 12、7
9、
 10、
10、 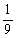
21、(本题满分13分)
已知函数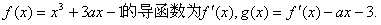
(I)当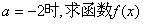 的单调区间;
的单调区间;
(II)若对满足 的取值范围;
的取值范围;
(III)若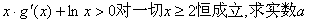 的取值范围。
的取值范围。
2010 届 高 三 三 校 联 考 试 题
数学答题卷(文史类)
20、(本题满分13分)
某种出口产品的关税税率t,市场价格x(单位:千元)与市场供应量p(单位:万件)之间近似满足关系式: ,其中k,b均为常数。当关税税率为75﹪时,若市场价格为5千元,则市场供应量均为1万元;若市场价格为7千元,则市场供应量约为2万件。
,其中k,b均为常数。当关税税率为75﹪时,若市场价格为5千元,则市场供应量均为1万元;若市场价格为7千元,则市场供应量约为2万件。
(I)试确定k、b的值;
(II)市场需求量q(单位:万件)与市场价格x近似满足关系式:q=2-x.p=q时,市场价格称为市场平衡价格。当市场平衡价格不超过4千元时,试确定关税税率的最大值。
19、(本题满分13分)
已知函数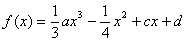 (a、c、d∈R)满足
(a、c、d∈R)满足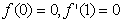 且
且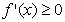 在R上恒成立。
在R上恒成立。
(I)求a、c、d的值;
(II)若 ,解不等式
,解不等式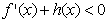 ;
;
18、(本题满分12分)
已知函数 的图象经过点
的图象经过点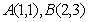 及
及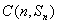 ,
, 为数列
为数列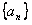 的前
的前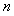 项和,
项和,
(I)求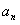 及
及 ;
;
(II)若数列 满足
满足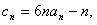 求数列
求数列 的前项和
的前项和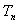
16、(本小题满分12分)
已知函数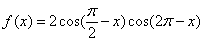 .
.
(I)求函数 的最小正周期;
的最小正周期;
(II)当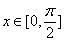 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
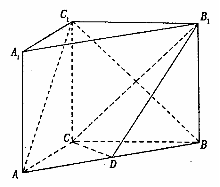
(17)、(本小题共12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4, 点D是AB的中点,
点D是AB的中点,
(I)求证:AC⊥BC1;
(II)求证:AC 1//平面CDB1;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com