
17、(2006年全国Ⅱ理18)某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.
解(1.) 




所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
|
P |
 |
 |
 |
 |
 的数学期望E(
的数学期望E( )=
)=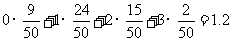
(2)P( )=
)=
16、(2006北京卷)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(Ⅰ) 应聘者用方案一考试通过的概率
p1=P(A·B· )+P(
)+P( ·B·C)+P(A·
·B·C)+P(A· ·C)+P(A·B·C)
·C)+P(A·B·C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.03+0.27+0.18+0.27=0.75.
(Ⅱ) 应聘者用方案二考试通过的概率
p2=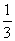 P(A·B)+
P(A·B)+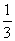 P(B·C)+
P(B·C)+ 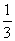 P(A·C)
P(A·C)
=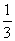 ×(0.5×0.6+0.6×0.9+0.5×0.9)=
×(0.5×0.6+0.6×0.9+0.5×0.9)=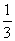 ×1.29=0.43
×1.29=0.43
15、(2007重庆理)某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆 元的保险金,对在一年内发生此种事故的每辆汽车,单位可获
元的保险金,对在一年内发生此种事故的每辆汽车,单位可获 元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为
元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为 ,
, ,
, ,且各车是否发生事故相互独立,求一年内该单位在此保险中:
,且各车是否发生事故相互独立,求一年内该单位在此保险中:
(Ⅰ)获赔的概率;
(Ⅱ)获赔金额 的分布列与期望.
的分布列与期望.
(18)(本小题13分)
解:设 表示第
表示第 辆车在一年内发生此种事故,
辆车在一年内发生此种事故, .由题意知
.由题意知 ,
, ,
, 独立,
独立,
且 ,
, ,
, .
.
(Ⅰ)该单位一年内获赔的概率为
 .
.
(Ⅱ) 的所有可能值为
的所有可能值为 ,
, ,
, ,
,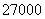 .
.
 ,
,



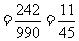 ,
,
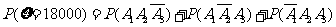


 ,
,

 .
.
综上知, 的分布列为
的分布列为




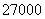



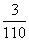

求 的期望有两种解法:
的期望有两种解法:
解法一:由 的分布列得
的分布列得

 (元).
(元).
解法二:设 表示第
表示第 辆车一年内的获赔金额,
辆车一年内的获赔金额, ,
,
则 有分布列
有分布列






故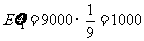 .
.
同理得 ,
,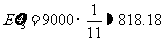 .
.
综上有 (元).
(元).
14、(2007年全国Ⅱ文19)从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.
(1)求从该批产品中任取1件是二等品的概率 ;
;
(2)若该批产品共100件,从中任意抽取2件,求事件 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率 .
.
(1)记 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,  表示事件“取出的2件产品中恰有1件二等品”. 则
表示事件“取出的2件产品中恰有1件二等品”. 则 互斥,且
互斥,且 ,故
,故


于是 . 解得
. 解得 (舍去).
(舍去).
(2)记 表示事件“取出的2件产品中无二等品”, 则
表示事件“取出的2件产品中无二等品”, 则 .
.
若该批产品共100件,由(1)知其中二等品有 件,故
件,故 .
.

13、(2007年福建文)甲、乙两名跳高运动员一次试跳 米高度成功的概率分别是
米高度成功的概率分别是 ,
, ,且每次试跳成功与否相互之间没有影响,求:
,且每次试跳成功与否相互之间没有影响,求:
(Ⅰ)甲试跳三次,第三次才成功的概率;
(Ⅱ)甲、乙两人在第一次试跳中至少有一人成功的概率;
(Ⅲ)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
解:记“甲第 次试跳成功”为事件
次试跳成功”为事件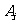 ,“乙第
,“乙第 次试跳成功”为事件
次试跳成功”为事件 ,依题意得
,依题意得 ,
,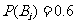 ,且
,且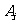 ,
, (
( )相互独立.
)相互独立.
(Ⅰ)“甲第三次试跳才成功”为事件 ,且三次试跳相互独立,
,且三次试跳相互独立,
 .
.
答:甲第三次试跳才成功的概率为 .
.
(Ⅱ)“甲、乙两人在第一次试跳中至少有一人成功”为事件 .
.
解法一: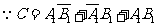 ,且
,且 ,
, ,
, 彼此互斥,
彼此互斥,



 .
.
解法二: .
.
答:甲、乙两人在第一次试跳中至少有一人成功的概率为 .
.
(Ⅲ)设“甲在两次试跳中成功 次”为事件
次”为事件 ,
,
“乙在两次试跳中成功 次”为事件
次”为事件 ,
,
 事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为
事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为 ,且
,且 ,
, 为互斥事件,
为互斥事件,
 所求的概率为
所求的概率为




答:甲、乙每人试跳两次,甲比乙的成功次数恰好多一次的概率为 .
.
12、(2008年全国Ⅱ理18)购买某种保险,每个投保人每年度向保险公司交纳保费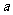 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有
10
000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为 .
.
(Ⅰ)求一投保人在一年度内出险的概率 ;
;
(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50 000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元).
解:各投保人是否出险互相独立,且出险的概率都是 ,记投保的10 000人中出险的人数为
,记投保的10 000人中出险的人数为 ,则
,则 .
.
(Ⅰ)记 表示事件:保险公司为该险种至少支付10 000元赔偿金,则
表示事件:保险公司为该险种至少支付10 000元赔偿金,则 发生当且仅当
发生当且仅当 ,
,

 ,
,
又 ,故
,故 .
.
(Ⅱ)该险种总收入为 元,支出是赔偿金总额与成本的和.
元,支出是赔偿金总额与成本的和.
支出
 ,
,
盈利
 ,
,
盈利的期望为  ,
,
由 知,
知, ,
,

 .
.



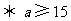 (元).
(元).
故每位投保人应交纳的最低保费为15元.
11、(2008年全国Ⅱ理理18)购买某种保险,每个投保人每年度向保险公司交纳保费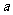 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为 .
.
(Ⅰ)求一投保人在一年度内出险的概率 ;
;
(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50 000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元).
解:各投保人是否出险互相独立,且出险的概率都是 ,记投保的10 000人中出险的人数为
,记投保的10 000人中出险的人数为 ,则
,则 .
.
(Ⅰ)记 表示事件:保险公司为该险种至少支付10 000元赔偿金,则
表示事件:保险公司为该险种至少支付10 000元赔偿金,则 发生当且仅当
发生当且仅当 , 2分
, 2分


 ,
,
又 ,故
,故 .········································································ 5分
.········································································ 5分
(Ⅱ)该险种总收入为 元,支出是赔偿金总额与成本的和.
元,支出是赔偿金总额与成本的和.
支出
 ,
,
盈利
 ,
,
盈利的期望为  ,················································· 9分
,················································· 9分
由 知,
知, ,
,

 .
.



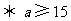 (元).
(元).
故每位投保人应交纳的最低保费为15元.……………………………………………… 12分
10、(2005年全国Ⅱ理15)设 为平面上过点
为平面上过点 的直线,
的直线, 的斜率等可能地取
的斜率等可能地取 ,用
,用 表示坐标原点到
表示坐标原点到 的距离,则随机变量
的距离,则随机变量 的数学期望
的数学期望 。
。
答案 
[解析]随机变量可能的取值为x1= ,x2=
,x2= ,x3=
,x3= ,x4=1,它们的概率分别为p1=
,x4=1,它们的概率分别为p1= ,p2=
,p2= ,p3=
,p3= ,p4=
,p4=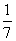 ,∴随机变量ζ的数学期望Eζ=
,∴随机变量ζ的数学期望Eζ= =
=
9、(2007年全国Ⅱ理14)在某项测量中,测量结果x服从正态分布N(1,s2)(s>0),若x在(0,1)内取值的概率为0.4,则x在(0,2)内取值的概率为 。
答案 0.8
[解析]在某项测量中,测量结果x服从正态分布N(1,s2)(s>0),正态分布图象的对称轴为x=1,x在(0,1)内取值的概率为0.4,可知,随机变量ξ在(1,2)内取值的概率于x在(0,1)内取值的概率相同,也为0.4,这样随机变量ξ在(0,2)内取值的概率为0.8。
8、(2007年湖北理)某篮运动员在三分线投球的命中率是 ,他投球10次,恰好投进3个球的概率 .(用数值作答)
,他投球10次,恰好投进3个球的概率 .(用数值作答)
答案 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com