
5、(2008年东北三省三校高三第一次联合模拟考试)
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号。若拿出球的标号是3的倍数,则得1分,否则得 分。
分。
(1)求拿4次至少得2分的概率;
(2)求拿4次所得分数 的分布列和数学期望。
的分布列和数学期望。
解(1)设拿出球的号码是3的倍数的为事件A,则 ,
, ,拿4次至少得2分包括2分和4分两种情况。
,拿4次至少得2分包括2分和4分两种情况。
 ,
, ,
,
(2) 的可能取值为
的可能取值为 ,则
,则
 ;
; ;
;
 ;
; ;
; ;
;
 分布列为
分布列为
|
P |
-4 |
-2 |
0 |
2 |
4 |
 |
 |
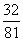 |
 |
 |
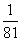 |

4、(2007石景山区高三二轮复习)一次单元测试由50个选择题构成,每个选择题有4个选项,其中恰有一个是正确的答案,每题选择正确得3分,不选或选错得0分,满分150分.学生甲选对任一题的概率为0.8,则该生在这次测试中成绩的期望值是_________,标准差是_____________.
答案 120 
3、(2008滨海高校月考)某人5上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已
知这组数据的平均数为10,方次差为2,则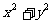 的值为
.
的值为
.
答案 208
2、(2007潍坊高三二轮复习)已知 ={(x,y)|x+y
={(x,y)|x+y 6,x
6,x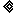 0,y
0,y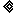 0},A={(x,y)|
x
0},A={(x,y)|
x 4,y
4,y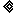 0,x-2y
0,x-2y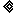 0},若向区域
0},若向区域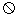 上随机投一点
上随机投一点 , 则点
, 则点 落入区域
落入区域 的概率为 ( )
的概率为 ( )
A.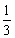 B.
B.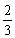 C.
C. D.
D.
答案 D
1、(2007南京模拟)6件产品中有4件合格品, 2件次品.为找出2件次品,每次任取一个检验,检验后不再放回,恰好经过4次检验找出2件次品的概率为 ( )
A.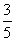 B.
B.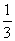 C.
C. D.
D.
答案 C
10、(2009上海九校联考)学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,
求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,
该小组没有参加过数学研究性学习活动的同学个数 是一个随机变量,
是一个随机变量,
求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
解:(1)记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的 ,
,
则其概率为 ………4分
………4分
答:恰好选到1个曾经参加过数学研究性学习活动的同学的概率为 ………5分
………5分
(2)随机变量
 ……6分
……6分
 ………8分
………8分
 ………10分
………10分
∴随机变量 的分布列为
的分布列为
 |
2 |
3 |
4 |
|
P |
 |
 |
 |
∴ ……12分
……12分
2007-2008年联考题
9、(2009上海卢湾区一模)(理)袋中有同样的球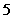 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机且不返回地摸球,每次摸
个黄色,现从中随机且不返回地摸球,每次摸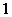 个,当两种颜色的球都被摸到时,即停止摸球,记随机变量
个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:.
为此时已摸球的次数,求:.
(1)随机变量 的概率分布律;(2)随机变量
的概率分布律;(2)随机变量 的数学期望与方差.
的数学期望与方差.
(文)袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机地摸
个黄色,现从中随机地摸 球,求:
球,求:
(1)红色球与黄色球恰好相等的概率(用分数表示结果)
(2)红色球多于黄色球的不同摸法的和数.
(理)解:(1)随机变量 可取的值为
可取的值为



得随机变量 的概率分布律为:
的概率分布律为:
 |
2 |
3 |
4 |
 |
 |
 |
 |
(2)随机变量 的数学期望为:
的数学期望为: ;
;
随机变量 的方差为:
的方差为:
(文)解:(1)
(2) .
.
8、(2009上海卢湾区4月模考)袋中有8个颜色不同,其它都相同的球,其中1个为黑球,3个为白球,4个为红球
(1)若从袋中一次摸出2个球,求所摸出的2个球恰为异色球的概率;
(2)若从袋中一次摸出3个球,且所摸得的3球中,黑球与白球的个数都没有超过红球的个数,记此时得到红球的个数为 ,求随机变量
,求随机变量 的概率分布律,并求
的概率分布律,并求 的数学期望
的数学期望 和方差
和方差 .
.
解:(1)摸出的2个球为异色球的不同摸法种数为 种,从8个球中摸出2个球的不同摸法种数为
种,从8个球中摸出2个球的不同摸法种数为 ,故所求概率为
,故所求概率为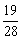 ; (6分)
; (6分)
(2)符合条件的摸法包括以下三种:一种是所摸得的3球中有1个红球,1个黑球,1个白球,共有 种不同摸法,一种是所摸得的3球中有2个红球,1个其它颜色球,共有
种不同摸法,一种是所摸得的3球中有2个红球,1个其它颜色球,共有 种不同摸法,一种是所摸得的3球均为红球,共有
种不同摸法,一种是所摸得的3球均为红球,共有 种不同摸法,故符合条件的不同摸法共有
种不同摸法,故符合条件的不同摸法共有 种.
种.
由题意随机变量 的取值可以为
的取值可以为 ,
, ,
, . 得随机变量
. 得随机变量 的概率分布律为:
的概率分布律为:
 |
1 |
2 |
3 |
||
 |
 |
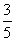 |

|
 ,
(13分)
,
(13分)
 .
(14分)
.
(14分)
7、(2009上海青浦区)市场上有一种“双色球”福利彩票,每注售价为2元,中奖概率为6.71%,一注彩票的平均奖金额为14.9元.如果小王购买了10注彩票,那么他的期望收益是 元.
答案  元
元
6、(2009上海普陀区)正方体骰子六个表面分别刻有 的点数. 现同时掷了两枚骰子,则得到的点数之和大于10的概率为
.
的点数. 现同时掷了两枚骰子,则得到的点数之和大于10的概率为
.
答案  ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com