7.[答案]C

[解析]由于水平面光滑,所以拉力F即为合外力,F随位移X的变化图象包围的面积即为F做的功, 设x₀处的动能为E_K由动能定理得: E_K-0===　 答案:C

6.[答案]BD

[解析]设月球引力对探测器做的功为W₁，

根据动能定理可得：－W+W₁＝0－E_k，

，可知，F_地＞F_月，

由W=Fs 虽然F是变力,但通过的距离一样,所以W＞W₁，E_k ＝W-W₁ < W　 故B选项正确。由于探测器在从地球到月球的过程中，地球引力越来越小，此过程中克服地球引力做的功为W，在从地球到达地月连线中点的过程中，探测器克服地球引力做的功要远大于1/2 W，而月球引力对探测器做的功很小，探测器的初动能若为1/2 W ，则到不了地月连线中点速度即减为0，所以探测器一定不能到达月球。 D选项也正确。

5.[答案]BC

[解析]O→C 由动能定理　 F_合S= 1/2 mv₁² = E_K1

A→C 由动能定理　 F_合S/2= 1/2 mv_A² = E_KA　

由功能关系得：E_K1 = 1/2 mv₁² =mgSsinθ+ Q

A点的势能为　　 E_PA= 1/2 mgSsinθ

E_KA=E_K1 / 2

∴　 E_KA> E_PA

4.[答案]D

[解析]在滑动的过程中，人受三个力重力做正功，势能降低B错；支持力不做功，摩擦力做负功，所以机械能不守恒，AC皆错，D正确。

3.[答案]A

[解析]上升的过程中,重力做负功,阻力做负功,由动能定理得

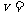
,,求返回抛出点的速度由全程使用动能定理重力做功为零,只有阻力做功为有,解得,A正确。

2.[答案]C

[解析]因为杆在转动，所以很多同学能分析到a球受到重力和杆对a的作用力，并习惯认为杆对a的作用力指向圆心O，与运动方向垂直，对小球a、b都不做功，而错选A、B。若我们能从整个系统去分析，会发现杆绕O点在竖直平面内无摩擦地转动，没有能量的损失，所以a、b和杆组成的系统机械能守恒。杆对a、b球的作用力是内力，a球下降过程中，b球的重力势能和动能都增加，所以b球的机械能增加，且b球重力对b球做负功，所以可以判断杆对b球做正功，b球的机械能才增加，从中可以判定B、D是错的。再由系统机械能守恒，b球的机械能增加，则a球的机械能减少，且a球重力对a球做正功，则杆对a球做负功，故A错。正确答案：C。

1.[答案]AD

[解析]重物从A点运动到B点，高度降低，重物的重力势能减少，因此很多同学只注意到重物从A运动到B时，重物速度增加，即重物的功能增加，故认为动能的增加量与重力势能的减少量相当，而判断重物机械能不变，错选C。若从整个系统去仔细分析会发现重物下降过程中，重物的动能增加，重力势力能减少，弹簧的弹性势能增加；而且在整个过程中，只有重力和弹簧弹力做功，重物与弹簧组成的系统机械能守恒。以B点为零势能点，则在A点系统的机械能只有重力势能，在B点系统的机械能为重物的动能和弹簧的弹性势能，且两处的机械能相等，所以可以判断重物的机械能减少，即C错，正确答案：A、D。

17.如图所示，在长为L的轻杆中点A和端点B各固定一质量均为m的小球，杆可绕无摩擦的轴O转动，使杆从水平位置无初速释放摆下。求当杆转到竖直位置时，轻杆对A、B两球分别做了多少功?

答案与解析

16.半径的竖直放置的圆轨道与水平直轨道相连接。如图所示。质量为的小球A以一定的初速度由直轨道向左运动，并沿圆轨道的内壁冲上去，如果A经过N点时的速度A经过轨道最高点M时对轨道的压力为，取．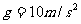

求：小球A从N到M这一段过程中克服阻力做的功W．

15.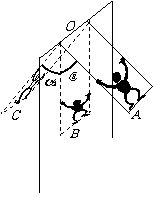如图是打秋千的示意图，最初人直立站在踏板上(A点所示)，绳与竖直方向成角，人的重心到悬点O的距离为；从A点向最低点B运动过程中，人由直立状态自然下蹲，在B点人的重心到悬点O的距离为；在最低点处，人突然由下蹲变成直立状态(人的重心到悬点O的距离恢复为)且保持该状态到最高点C.设人的质量为m，踏板和绳的质量不计，空气阻力不计.求：

　(1)人刚到最低点B还处于下蹲状态时，两根绳中的总拉力F为多大？

(2)人到达左端最高点C时，绳与竖直方向的夹角为多大？(用反三角函数表示)