
3.(2009福州三中)已知等差数列{an}的前n项和为Sn,若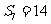 ,则
,则 的值为( )
的值为( )
A.2 B.4 C.7 D.8
答案 B
2. (北京市西城区2009年4月高三一模抽样测试理) 若数列 是公比为4的等比数列,且
是公比为4的等比数列,且 ,则数列
,则数列 是( )
是( )
A.
公差为2的等差数列
B. 公差为 的等差数列
的等差数列 
C.
公比为2的等比数列
D. 公比为 的等比数列
的等比数列
答案 A
1.(北京市朝阳区2009年4月高三一模理)各项均不为零的等差数列 中,若
中,若 ,则
,则 等于 ( )
等于 ( )
A.0 B.2 C.2009 D.4018
答案 D
2009年联考题
27.(2005福建)已知{ }是公比为q的等比数列,且
}是公比为q的等比数列,且 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{ }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
解:(Ⅰ)由题设
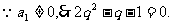

(Ⅱ)若
当 故
故
若
当
故对于
26.(2005北京)数列{an}的前n项和为Sn,且a1=1, ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II) 的值.
的值.
解:(I)由a1=1, ,n=1,2,3,……,得
,n=1,2,3,……,得
 ,
, ,
, ,
,
由 (n≥2),得
(n≥2),得 (n≥2),
(n≥2),
又a2= ,所以an=
,所以an= (n≥2),
(n≥2),
∴ 数列{an}的通项公式为
25..(2008湖北).已知数列 和
和 满足:
满足:
 ,
, 其中
其中 为实数,
为实数, 为正整数.
为正整数.
(Ⅰ)对任意实数 ,证明数列
,证明数列 不是等比数列;
不是等比数列;
(Ⅱ)试判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)设 ,
, 为数列
为数列 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有
 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
本小题主要考查等比数列的定义、数列求和、不等式等基础知识和分类讨论的思想,考查综合分析问题的能力和推理认证能力,(满分14分)
(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
 矛盾.
矛盾.
所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1( an-2n+14)
an-2n+14)
= (-1)n·(an-3n+21)=-
(-1)n·(an-3n+21)=- bn
bn
又b1x-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18) ≠0,由上可知bn≠0,∴ (n∈N+).
(n∈N+).
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,- 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn=
-(λ+18)·(- )n-1,于是可得
)n-1,于是可得
Sn=-
要使a<Sn<b对任意正整数n成立,
即a<- (λ+18)·[1-(-
(λ+18)·[1-(- )n]〈b(n∈N+)
)n]〈b(n∈N+)
 ①
①
当n为正奇数时,1<f(n)
∴f(n)的最大值为f(1)= ,f(n)的最小值为f(2)=
,f(n)的最小值为f(2)=  ,
,
于是,由①式得 a<-
a<- (λ+18),<
(λ+18),<
当a<b 3a时,由-b-18
3a时,由-b-18 =-3a-18,不存在实数满足题目要求;
=-3a-18,不存在实数满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<2.
24.(2008江西卷)数列 为等差数列,
为等差数列, 为正整数,其前
为正整数,其前 项和为
项和为 ,数列
,数列 为等比数列,且
为等比数列,且 ,数列
,数列 是公比为64的等比数列,
是公比为64的等比数列, .
.
(1)求 ;
;
(2)求证 .
.
解:(1)设 的公差为
的公差为 ,
, 的公比为
的公比为 ,则
,则 为正整数,
为正整数,
 ,
,
依题意有 ①
①
由 知
知 为正有理数,故
为正有理数,故 为
为 的因子
的因子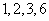 之一,
之一,
解①得
故
(2)
∴


23.(2008四川卷). 设数列 的前
的前 项和为
项和为 ,已知
,已知
(Ⅰ)证明:当 时,
时,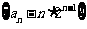 是等比数列;
是等比数列;
(Ⅱ)求 的通项公式
的通项公式
解 由题意知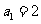 ,且
,且

两式相减得
即 ①
①
(Ⅰ)当 时,由①知
时,由①知
于是

又 ,所以
,所以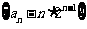 是首项为1,公比为2的等比数列。
是首项为1,公比为2的等比数列。
(Ⅱ)当 时,由(Ⅰ)知
时,由(Ⅰ)知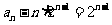 ,即
,即
当 时,由由①得
时,由由①得



因此

得
22.(2006湖南)数列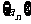 满足:
满足: ,2,3….则
,2,3….则 .
.
答案 
解析 数列 满足:
满足:
 ,2,3…,该数列为公比为2的等比数列,
,2,3…,该数列为公比为2的等比数列,
 ∴
∴  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com