
1.( 上海市部分重点中学高三第一次联考)
等差数列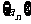 的前n项和
的前n项和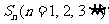 当首项
当首项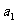 和公差d变化时,若
和公差d变化时,若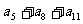 是一个定值,则下列各数中为定值的是―――――――――( )
是一个定值,则下列各数中为定值的是―――――――――( )
A、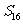 B.
B. S
S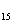 C、
C、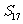 D、
D、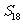
答案 B
3.(2009上海八校联考)已知点列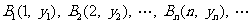
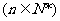 顺次为直线
顺次为直线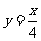 上的点,点列
上的点,点列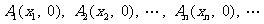
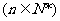 顺次为
顺次为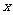 轴上的点,其中
轴上的点,其中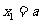
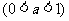 ,对任意的
,对任意的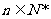 ,点
,点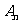 、
、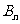 、
、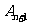 构成以
构成以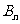 为顶点的等腰三角形。
为顶点的等腰三角形。
(1)证明:数列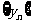 是等差数列;
是等差数列;
(2)求证:对任意的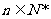 ,
, 是常数,并求数列
是常数,并求数列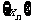 的通项公式;
的通项公式;
(3)对上述等腰三角形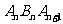 添加适当条件,提出一个问题,并做出解答。
添加适当条件,提出一个问题,并做出解答。
(根据所提问题及解答的完整程度,分档次给分)
解: (1)依题意有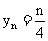 ,于是
,于是 .
.
所以数列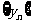 是等差数列.
是等差数列.
 .4分
.4分
(2)由题意得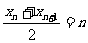 ,即
,即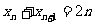 , (
, (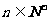 )
①
)
①
所以又有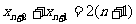 .
②
.
②
由②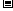 ①得:
①得: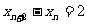 , 所以
, 所以 是常数.
是常数.  6分
6分
由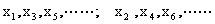 都是等差数列.
都是等差数列.
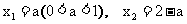 ,那么得
,那么得  ,
,
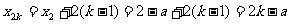 . (
. (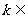
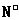
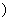
 8分
8分
故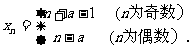
 10分
10分
(3) 提出问题①:若等腰三角形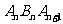 中,是否有直角三角形,若有,求出实数
中,是否有直角三角形,若有,求出实数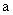
提出问题②:若等腰三角形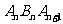 中,是否有正三角形,若有,求出实数
中,是否有正三角形,若有,求出实数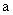
解:问题①  11分
11分
当 为奇数时,
为奇数时,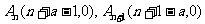 ,所以
,所以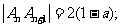
当 为偶数时,
为偶数时,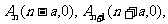 所以
所以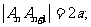
作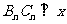 轴,垂足为
轴,垂足为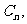 则
则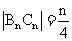 ,要使等腰三角形
,要使等腰三角形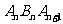 为直角三角形,必须且只须:
为直角三角形,必须且只须: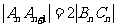 .
.
 13分
13分
当 为奇数时,有
为奇数时,有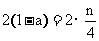 ,即
,即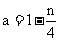 ①
①
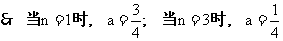 , 当
, 当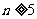 ,
, 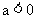 不合题意.
不合题意. 15分
15分
当 为偶数时,有
为偶数时,有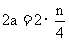 ,
,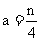 ,同理可求得
,同理可求得 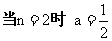
当 时,
时,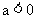 不合题意.
不合题意.  17分
17分
综上所述,使等腰三角形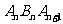 中,有直角三角形,
中,有直角三角形,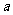 的值为
的值为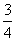 或
或 或
或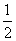 .
.
 18分
18分
解:问题②  11分
11分
当 为奇数时,
为奇数时,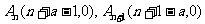 ,所以
,所以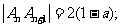
当 为偶数时,
为偶数时,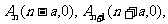 所以
所以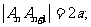
作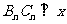 轴,垂足为
轴,垂足为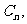 则
则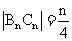 ,要使等腰三角形
,要使等腰三角形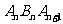 为正三角形,必须且只须:
为正三角形,必须且只须: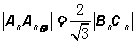 .
.
 13分
13分
当 为奇数时,有
为奇数时,有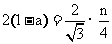 ,即
,即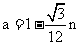 ①
①
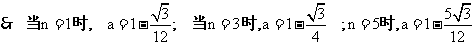 , 当
, 当 时,.
时,. 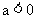 不合题意.
不合题意.  15分
15分
当 为偶数时,有
为偶数时,有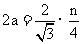 ,
,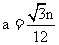 ,同理可求得
,同理可求得 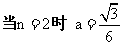 .
.
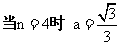 ;
;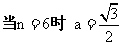 ;当
;当 时,
时,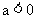 不合题意.
不合题意. 17分
17分
综上所述,使等腰三角形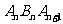 中,有正三角形,
中,有正三角形,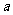 的值为
的值为
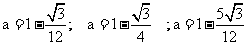 ;
;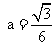 ;
;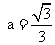 ;
;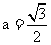
 18分
18分
2007--2008年联考题
即- <λ<1,又λ≠0,λ为整数,
<λ<1,又λ≠0,λ为整数,
∴λ=-1,使得对任意n∈N*,都有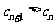 . 12分
. 12分
2.(2009上海青浦区)设数列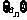 的前
的前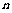 和为
和为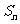 ,已知
,已知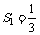 ,
,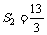 ,
,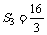 ,
,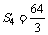 ,
,
一般地,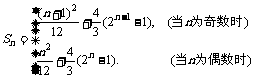 (
(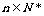 ).
).
(1)求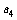 ;
;
(2)求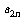 ;
;
(3)求和: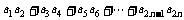 .
.
(1)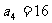 ;
……3分
;
……3分
(2)当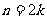 时,(
时,(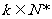 )
)
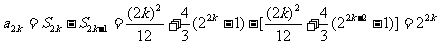 , ……6分
, ……6分
所以,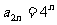 (
(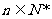 ).
……8分
).
……8分
(3)与(2)同理可求得: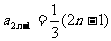 ,
……10分
,
……10分
设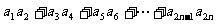 =
= ,
,
则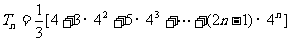 ,(用等比数列前n项和公式的推导方法)
,(用等比数列前n项和公式的推导方法)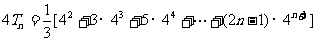 ,相减得
,相减得
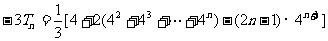 ,所以
,所以
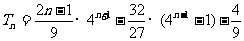 .
……14分
.
……14分
1.(2009滨州一模)已知曲线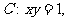 过
过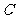 上一点
上一点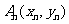 作一斜率为
作一斜率为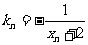 的直线交曲线
的直线交曲线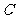 于另一点
于另一点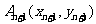 ,点列
,点列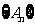 的横坐标构成数列
的横坐标构成数列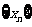 ,其中
,其中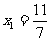 .
.
(I)求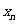 与
与 的关系式;
的关系式;
(II)令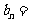
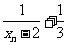 ,求证:数列
,求证:数列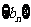 是等比数列;
是等比数列;
(III)若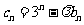 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立。
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立。
(1) 解:过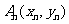 的直线方程为
的直线方程为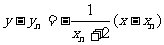
联立方程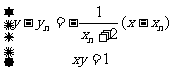 消去
消去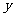 得
得
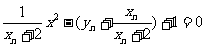
∴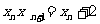
即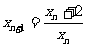
(2)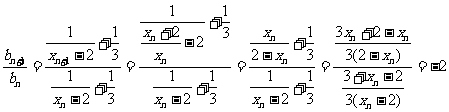
∴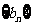 是等比数列
是等比数列
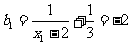 ,
,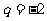 ;
;
(III) 由(II)知,
由(II)知,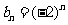 ,要使
,要使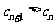 恒成立由
恒成立由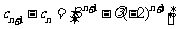
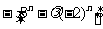 =
=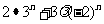 >0恒成立,
>0恒成立,
即(-1)nλ>-( )n-1恒成立.
)n-1恒成立.
ⅰ。当n为奇数时,即λ<( )n-1恒成立.
)n-1恒成立.
又( )n-1的最小值为1.∴λ<1. 10分
)n-1的最小值为1.∴λ<1. 10分
ⅱ。当n为偶数时,即λ>-( )n-1恒成立,
)n-1恒成立,
2.((2009上海八校联考)在数列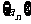 中,
中,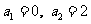 ,且
,且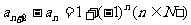 ,
,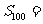 _________。
_________。
答案 2550
1.(2009上海十四校联考)若数列 为“等方比数列”。则“数列
为“等方比数列”。则“数列 是等方比数列”是“数列
是等方比数列”是“数列 是等方比数列”的
条件
是等方比数列”的
条件
3.(2009聊城一模)两个正数a、b的等差中项是5,等比例中项是4,若a>b,则双曲线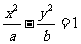 的离心率e等于 ( )
的离心率e等于 ( )
A. B.
B.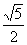 C.
C.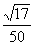 D.
D.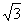
答案B
2.(2009上海十四校联考)无穷等比数列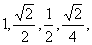 …各项的和等于 ( )
…各项的和等于 ( )
A.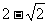 B.
B.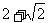 C.
C.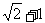 D.
D.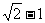
答案B
1.(2009滨州一模)等差数列 中,
中,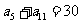 ,
,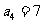 ,则
,则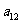 的值为
的值为
A.15 B.23 C.25 D.37
答案 B
14.(2009常德期末)已知数列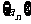 的前n项和为
的前n项和为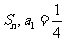 且
且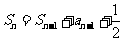 ,数列
,数列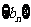 满足
满足 且
且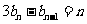
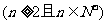 .
.
(1)求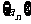 的通项公式;
的通项公式;
(2)求证:数列 为等比数列;
为等比数列;
(3)求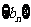 前n项和的最小值.
前n项和的最小值.
解: (1)由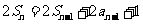 得
得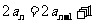 ,
,  ……2分
……2分
∴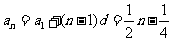 ……………………………………4分
……………………………………4分
(2)∵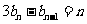 ,∴
,∴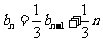 ,
,
∴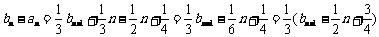 ;
;
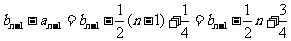
∴由上面两式得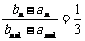 ,又
,又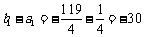
∴数列 是以-30为首项,
是以-30为首项,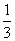 为公比的等比数列.…………………8分
为公比的等比数列.…………………8分
(3)由(2)得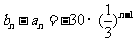 ,∴
,∴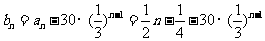
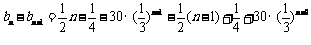
=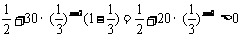 ,∴
,∴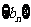 是递增数列 ………11分
是递增数列 ………11分
当n=1时,  <0;当n=2时,
<0;当n=2时, 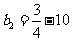 <0;当n=3时,
<0;当n=3时, 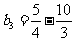 <0;当n=4时,
<0;当n=4时, 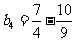 >0,所以,从第4项起的各项均大于0,故前3项之和最小.
>0,所以,从第4项起的各项均大于0,故前3项之和最小.
且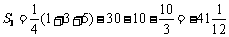 …………………………13分
…………………………13分
9月份更新
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com