
1、一艘小船沿一定航向渡河,由于水流的作用,此时小船恰能沿垂直河岸方向抵达对岸。今保持小船的航向和动力的大小不变,则: ( )
A.若水流速度减小,则小船抵达对岸时将偏向下游
B.若水流速度减小,则小船的合速度增大
C.若水流速度增大,则小船抵达对岸时间减少
D.若水流速度增大,则小船的合速度不变
9. 如图甲所示,质量分别为m=1kg,M=2kg的A、B两个小物块用轻弹簧相连而静止在光滑水平面上,在A的左侧某处另有一个质量也为m=1kg的小物块C以v0=4m/s的速度正对A向右匀速运动,一旦与A接触就将粘合在一起运动,若在C与A接触前,使A获得一初速度vA0,并从此时刻开始计时,向右为正方向,其速度随时间变化的图像如图乙所示(C与A未接触前),弹簧始终未超过弹簧性限度。
⑴在C与A接触前,当A的速度分别为6m/s、2m/s、–2m/s时,求对应状态下B的速度,并在此基础上在图乙中粗略画出B的速度随时间变化图像;
⑵若C在A的速度为vA时与A接触,在接触后的运动过程中弹簧弹性势能的最大值为Ep,求EP的变化范围。
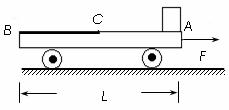
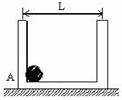
8. 如图所示,光滑水平地面上停着一辆平板车,其质量为2m,长为L,车右端(A点)有一块静止的质量为m的小金属块.金属块与车间有摩擦,以中点C为界, AC段与CB段动摩擦因数不同,分别为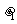 、
、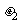 。现给车施加一个向右的水平恒力,使车向右运动,同时金属块在车上开始滑动,当金属块滑到中点C时,即撤去这个力。已知撤去力的瞬间,金属块的速度为v0,车的速度为2v0,最后金属块恰停在车的左端(B点)。求
。现给车施加一个向右的水平恒力,使车向右运动,同时金属块在车上开始滑动,当金属块滑到中点C时,即撤去这个力。已知撤去力的瞬间,金属块的速度为v0,车的速度为2v0,最后金属块恰停在车的左端(B点)。求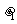 与
与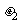 的比值。
的比值。
7. 航天飞机,可将物资运送到空间站,也可维修空间站出现的故障。
(1)若已知地球半径为R,地球表现重力加速度为g,某次维修作业中,与空间站对接的航天飞机的速度计显示飞机的速度为v,则该空间站轨道半径R′为多大?
(2)为完成某种空间探测任务,在空间站上发射的探测器通过向后喷气而获得反冲力使其启动。已知探测器的质量为M,每秒钟喷出的气体质量为m,为了简化问题,设喷射时探测器对气体做功的功率恒为P,在不长的时间内探测器的质量变化较小,可以忽略不计。求喷气t秒后探测器获得的动能是多少?
6.电动机通过一绳子吊起质量为8 kg的物体,绳的拉力不能超过120 N,电动机的功率不能超过1200 W,要将此物体由静止起用最快的方式吊高90m(已知此物体在被吊高接近90 m时,已开始以最大速度匀速上升)所需时间为多少?(g=10 m/s2)
5. 在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率Vc=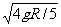 ,则下述正确的是 ( )
,则下述正确的是 ( )
A.此球的最大速率是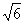 Vc
Vc
B.小球到达C点时对轨道的压力是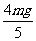
C.小球在任一直径两端点上的动能之和相等
D.小球沿圆轨道绕行一周所用的时间小于π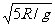
4. 子弹在射入木块前的动能为E1,动量大小为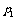 ;射穿木板后子弹的动能为E2,动量大小为
;射穿木板后子弹的动能为E2,动量大小为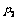 。若木板对子弹的阻力大小恒定,则子弹在射穿木板的过程中的平均速度大小为( )
。若木板对子弹的阻力大小恒定,则子弹在射穿木板的过程中的平均速度大小为( )
A.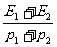 B.
B.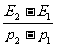 C.
C.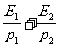 D.
D.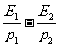
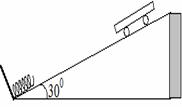
3. 如图为某探究活动小组设计的节能运动系统。斜面轨道倾角为30°,质量为M的小车与轨道的动摩擦因数为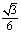 。小车在轨道顶端时,自动装货装置将质量为m的货物装入小车,然后小车载着货物沿轨道无初速滑下,将轻弹簧压缩至最短时,自动卸货装置立即将货物卸下,然后小车恰好被弹回到轨道顶端,之后重复上述过程。根据以上条件,下列选项正确的是( )
。小车在轨道顶端时,自动装货装置将质量为m的货物装入小车,然后小车载着货物沿轨道无初速滑下,将轻弹簧压缩至最短时,自动卸货装置立即将货物卸下,然后小车恰好被弹回到轨道顶端,之后重复上述过程。根据以上条件,下列选项正确的是( )
A.m=M
B.m=2M
C.小车不与弹簧接触时,上滑的加速度大于下滑的加速度
D.在小车与货物从顶端滑到最低点的过程中,减少的重力势能全部转化为弹簧的弹性
2.从空中A点以E1 = 1J的初动能水平抛出一小球,小球刚要落地时的动能E2 = 5J,落地点在B点。不计空气阻力,则A、B两点的连线与水平面间的夹角为( )
A.30° B.37° C.45° D.60°
点评:
本题考点: 功能关系
思路分析: 受力分析然后做功分析再找出功与能量的关系
例题2如图所示,两根间距为L=1m的金属导轨MN和PQ,电阻不计,左端向上弯曲,其余水平,水平导轨左端有宽度为d=2m,方向竖直向上的匀强磁场i,右端有另一磁场ii,其宽度为d,但方向竖直向下,两者B均为1T,有两根质量均为m=1kg,电阻均为R=1Ω,的金属棒a与b与导轨垂直放置,b棒置于磁场ii中点C,D处,导轨除C,D外(对应距离极短)其余均为光滑,两处对棒可产生总的最大静摩擦力为自重的0.2倍,a棒从弯曲导轨某处由静止释放,当只有一根棒做切割磁感线运动时,它速度的减小量与它在磁场中通过的距离成正比,即Δv∝Δx(1)若棒a从某一高度释放,则棒a进入磁场i时恰能使棒b运动,判断棒b运动方向并求出释放高度;(2)若将棒a从高度为0.2m的某处释放结果棒a以1m/s的速度从磁场i中穿出求两棒即将相碰时棒b所受的摩擦力; (3)若将棒a从高度1.8m某处释放经过一段时间后棒a从磁场i穿出的速度大小为4m/s,且已知棒a穿过磁场时间内两棒距离缩短2.4m,求棒a从磁场i穿出时棒b的速度大小及棒a穿过磁场i所需的时间(左为a,右为b)

解析:
⑴由右手定则可以得到棒a的在靠近我们一侧,所以棒b的电流向里。由左手定则可以得到棒b受到的安培力向左,则b要动也得向左动。
对b:BIL=μmg I=E/2R
对a:E=BLV
由上面三个式子得到:V=4m/s
对a下落动能定理: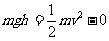 得到h=0.8m
得到h=0.8m
⑵现在高度为0.2m小于第一问中的0.8m,即棒a进入磁场i的速度达不到让棒b运动的情况,所以相碰之前b一直没有动。
对a下落动能定理: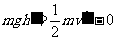 得到v=2m/s
得到v=2m/s
对a下落动能定理: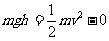 得到h=0.8m
得到h=0.8m
对a穿过磁场i:Δv=kΔx 得到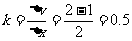
对a进入磁场ii到相碰:Δv/=kΔx/得到碰时速度V/为0.5m/s
此时算出电动势0.5V、电流0.25A、安培力0.25A最终得到静摩擦力为0.25N
⑶现在高度为1.8m大于第一问中的0.8m,即棒a进入磁场i的速度达到让棒b运动的情况,所以b动了。题中说“已知棒a穿过磁场时间内两棒距离缩短2.4m”推出b向左运动了0.4m
对a下落动能定理: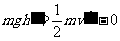 得到
得到 =6m/s
=6m/s
对a对穿越磁场i过程动能定理: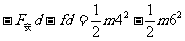
对b运动过程动能定理: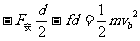
解得:vb=2m/s
对a对穿越磁场i过程动量定理: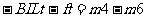
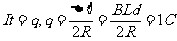 得t=0.5s
得t=0.5s
例题3 如图所示,水平面放一质量为0.5kg的长条形金属盒,盒宽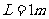 ,它与水平面间的动摩擦因数是0.2,在盒的A端有一个与盒质量相等的小球。球与盒无摩擦,现在盒的A端迅速打击一下金属盒,给盒以
,它与水平面间的动摩擦因数是0.2,在盒的A端有一个与盒质量相等的小球。球与盒无摩擦,现在盒的A端迅速打击一下金属盒,给盒以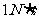 的向右的冲量,设球与盒间的碰撞没有能量损失,且碰撞时间极短,求球与盒组成的系统从开始运动到完全停止所用时间。(
的向右的冲量,设球与盒间的碰撞没有能量损失,且碰撞时间极短,求球与盒组成的系统从开始运动到完全停止所用时间。(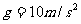 )
)
解析:
设打击后金属盒的速度为v0,由I=mv0解得: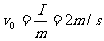
由于盒子与球碰撞时间极短,因而盒子与球组成的系统动量应该守恒,则有:
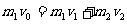
由于碰撞过程没有能量损失,则有:
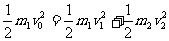
且有: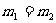
解得: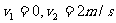 (即质量相同的两个物体发生弹性碰撞时速度互换)
(即质量相同的两个物体发生弹性碰撞时速度互换)
球在盒子内做匀速运动,经时间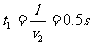 在盒子右端与盒子相碰,由动量守恒定律和能量守恒定律可得碰撞后盒子的速度为:
在盒子右端与盒子相碰,由动量守恒定律和能量守恒定律可得碰撞后盒子的速度为:
盒子克服摩擦做功,则由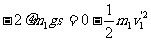 ,即有:
,即有: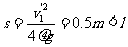 ,说明盒子停下之前球不再与盒子相碰,设盒子滑行的时间为
,说明盒子停下之前球不再与盒子相碰,设盒子滑行的时间为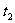 ,由动量定理有:
,由动量定理有:
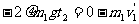
则可知:
球与盒组成的系统从开始运动到完全停止所用时间为:

例题4如图所示,一物块以6 m/s的初速度从曲面A点下滑,运动到B点速度仍为6 m/s;若物体以5 m/s的初速度仍由A点下滑,则它运动到B点时的速度( )
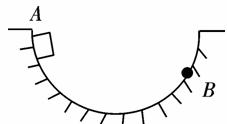
A.大于5 m/s
B.等于5 m/s
C.小于5 m/s
D.条件不足,无法计算
解析:
物块由A点运动到B点,重力做正功,摩擦力做负功,由动能定理有: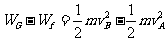
当物块初速度为6 m/s时,物块由A点运动到B点的过程,速度大小不变,动能变化为零,WG=Wf。由于物块做圆周运动,速度越大,所需向心力越大,曲面对物块的支持力越大,摩擦力越大,在相同路程的条件下,摩擦力的功越大,所以,当物块初速度为5 m/s时,摩擦力的功比初速度为6 m/s时要小,WG>Wf ,到达B点的速度将大于5 m/s.
点评:
重力做功与路径无关,只与物体所处的初末位置有关.摩擦力做功与物体表面粗糙程度、正压力大小、路径有关,当物体运动路程一定时,对同一路面,在相同路程的条件下,曲面对物块的支持力越大,摩擦力越大,摩擦力的功越大。
例题5一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的。今把质点从O点的正上方离O点的距离为8R/9的o1点以水平的速度v0=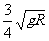 抛出,如图所示。试求;
抛出,如图所示。试求;
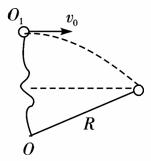
(1)轻绳即将伸直时,绳与竖直方向的夹角为多少?
(2)当质点到达O点的正下方时,绳对质点的拉力为多大?
解析:
第一过程:质点做平抛运动.设绳即将伸直时,绳与竖直方向的夹角为θ,如题图所示,
则:v0t=Rsinθ,gt2/2=8R/9-Rcosθ其中v0=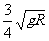
联立解得θ=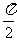 ,t=
,t=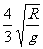 .
.
第二过程:绳绷直过程.绳绷直时,绳刚好水平,如图所示。
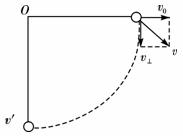
由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度v⊥,且v⊥=gt= 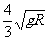
第三过程:小球在竖直平面内做圆周运动。设质点到达O点正下方时,速度为v′,根据机械能守恒定律有:mv/2/2=mv⊥2/2+mg·R
设此时绳对质点的拉力为T,则T-mg=m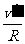 ,联立解得:T=43mg/9.
,联立解得:T=43mg/9.
答案:(1)90° (2)T=43mg/9.
点评:
质点的运动可分为三个过程:质点做平抛运动;绳绷直过程;小球在竖直平面内做圆周运动。解答时容易忽视在绳被拉直瞬时过程中机械能的瞬时损失。
针对性训练:
1、物体在运动过程中重力做了-10J功,则可以得出( )
A.物体克服重力做功10J B.物体的重力势能一定增加10J
C.物体的动能一定增加10J D.物体的机械能一定不变
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com