
2、什么叫做映射?
|
3、举例说明什么叫一一映射。 4、映射和函数有什么样的关系? 课堂练习: 下列哪些对应是从集合A到集合B的映射? (1)A={P | P是数轴上的点},B=R,对应关系f:数轴上的点与它所代表的实数对应; (2)A={ P | P是平面直角体系中的点},B={(x,y)| x∈R,y∈R},对应关系f:平面直角体系中的点与它的坐标对应; (3)A={三角形},B={x | x是圆},对应关系f:每一个三角形都对应它的内切圆; (4)A={x | x是新华中学的班级},B={x | x是新华中学的学生},对应关系f:每一个班级都对应班里的学生. 教材P36练习A 1、 |
|
学习方法指导: 通过本节课同学们应该充分了解映射和函数的从属关系,“函数是特殊的映射”或者从集合的角度看,函数是映射的子集。只有更深层次的了解映射,才能在今后做综合习题时做到成竹在胸。 |
|
课后作业:P36练习B 3、4、5 |
|
学生作业后的反思与体会: |
18.已知全集U=R,集合A=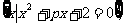
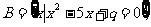
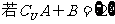 ,试用列举法表示集合A
,试用列举法表示集合A
19 .已知全集U={x|x
.已知全集U={x|x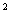 -3x+2≥0},A={x||x-2|>1},B=
-3x+2≥0},A={x||x-2|>1},B=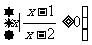 ,求C
,求C A,C
A,C B,A∩B,A∩(C
B,A∩B,A∩(C B),(C
B),(C A)∩B
A)∩B
20 .关于实数x的不等式
.关于实数x的不等式 与x
与x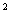 -3(a+1)x+2(3a+1)≤0
-3(a+1)x+2(3a+1)≤0
(a∈R)的解集依次为A,B 求使
求使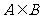 成立的实数a的取值范围
成立的实数a的取值范围
17.已知集合A=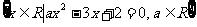
1)若A是空集,求a的取值范围;
2)若A中只有一个元素,求a的值,并把这个元素写出来;
3)若A中至多只有一个元素,求a的取值范围
15.已知集合A= 用列举法表示集合A= 
16 已知U=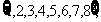
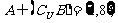
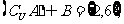
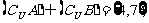 则集合A=
则集合A=

14.不等式|x-1|>-3的解集是 
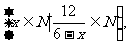
13.集合P=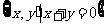 ,Q=
,Q=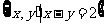 ,则A∩B=
,则A∩B= 
12.定义A-B={x|x A且x
A且x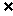 B}, 若A={1,2,3,4,5},B={2,3,6},
B}, 若A={1,2,3,4,5},B={2,3,6},
则A-(A-B)等于( )
(A)B (B)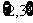 (C)
(C) 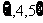 (D)
(D) 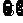
11、如右图,那么阴影部分所表示的集合是( )
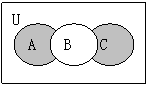 (A)
(A)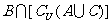 (B)
(B)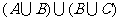
(C)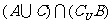 (D)
(D)
10、满足条件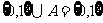 的所有集合A的个数是( )
的所有集合A的个数是( )
(A)1个 (B)2个 (C)3个 (D)4个
9、已知集合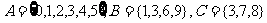 ,则
,则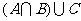 等于
等于
(A){0,1,2,6} (B){3,7,8,}
(C){1,3,7,8} (D){1,3,6,7,8}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com