
4、函数的零点的性质:
(1)如果函数的图象是连续的,当它通过零点(不是二重零点)时,函数值 ;
(2)如果函数的图象是连续的,那么相邻两个零点之间的所有函数值 ;
(3)如果函数y=f(x)在一个区间[a,b]上的图象连续不间断,并且在它的两个端点处的函数值异号,即f(a)f(b)<0,则这个函数在这个区间上
,即存在一点
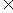 [a,b]使
,这样的零点常称作
,有时函数通过零点时不变号,这样的零点称作
;
[a,b]使
,这样的零点常称作
,有时函数通过零点时不变号,这样的零点称作
;
3、函数的零点也可以理解为 ;
2、确定函数y=f(x)的零点,就是 ;
1、一般地,如果函数y=f(x)在实数x=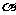 处的值
,即
,则
处的值
,即
,则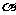 叫做这个函数的零点。
叫做这个函数的零点。
2、体会函数的零点的实质及图象穿过和不穿过的两种情形。
尝试练习:
2、理解掌握二次函数的零点指的什么,二重零点又指的什么;
3.判断函数单调性的方法步骤
例1.证明函数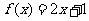 ,在
,在 上是增函数.
上是增函数.
例2证明函数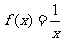 ,在区间
,在区间 和
和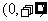 上分别是减函数
上分别是减函数
练习:46页练习A
|
学习方法指导:函数的单调性一般是先根据图象判断,再利用定义证明.画函数图象通常借助计算机,求函数的单调区间时必须要注意函数的定义域,单调性的证明一般分五步: 取 值 → 作 差 → 变 形 → 定 号 → 下结论 |
|
课后作业: 52页 6 |
|
学生作业后的反思与体会: |
2.函数的单调性定义
1.增函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com