4．多面体中表面上两点的最短距离。

多面体中表面上两点的最短距离，就是其平面展开图中，连结这两点的线段长度，这是立体几何中求最短距离的基本依据(球面上两点间的距离除外)。

3．正棱锥的侧面积与底面积的关系。

正棱锥：S_底=S_侧cosα

2．正棱锥的计算问题。应抓住四个直角三角形和两个角。四个直角三角形，即正棱锥的高、侧棱及其在底面上的射影、斜高及其在底面上的射影、底面边长的一半组成的四个直角三角形。两个角，即侧棱与底面所成的线面角，侧面与底面所成的二面角。四个直角三角形所围成的几何体称之为“四直角四面体”，它是解决棱锥计算问题的基本依据，必须牢固掌握。

1．割补法。它是通过“割”与“补”等手段，将不规则的几何体转化为规则的几何体，是一种常用的转化方法。

4．球

S_球=4πR²　 V_球=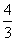πR³

3．棱柱、棱锥的侧面积与体积

S_正棱柱侧=Ch′　　 S_正棱锥侧= 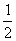Ch′　 V_柱体=S h′　　 V_锥体=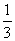Sh′

2．棱锥

1．棱柱

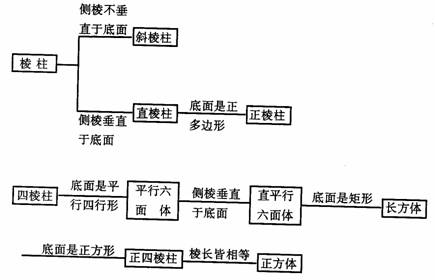
3．了解多面体的概念，能正确画出棱柱、正棱锥的直观图。

对于截面问题，只要求会解决与几种特殊的截面(棱柱、棱锥的对角面，棱柱的直截面，球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题。

1．理解棱柱、棱锥、球及其有关概念和性质。

掌握直棱柱、正棱锥、球的表面积和体积公式，并能运用这些公式进行计算。