
8.设地球半径为R,在北纬30°圈上有甲、乙两地,它们的经度差为120°,那么这两地间的纬线之长为( )
A.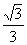 πR B.
πR B. πR C.πR D.2πR
πR C.πR D.2πR
7.图8-23中多面体是过正四棱柱的底面正方形ABCD的顶点A作截面AB1C1D1而截得的,且B1B=D1D。已知截面AB1C1D1与底面ABCD成30°的二面角,AB=1,则这个多面体的体积为( )
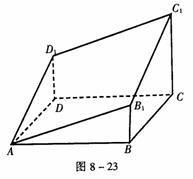
A.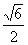 B.
B.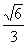 C.
C. D.
D.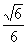
6.棱锥被平行于底面的平面所截,当截面分别平分棱锥的侧棱、侧面积、体积时,相应的截面面积分别为S1、S2、S3,则( )
A.S1<S2<S3 B.S3<S2<S1 C.S2<S1<S3 D.S1<S3<S2
5.把一个半径为R的实心铁球熔化铸成两个小球(不计损耗),两个小球的半径之比为1∶2,则其中较小球半径为( )
A.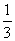 R B.
R B.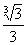 R C.
R C.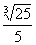 R D.
R D.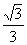 R
R
4.长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,则这个球面的表面积为( )
A.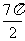 B.56π C.14π D.64π
B.56π C.14π D.64π
3.一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面( )
A.必定都不是直角三角形 B.至多有一个直角三角形
C.至多有两个直角三角形 D.可能都是直角三角形
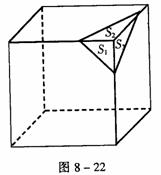
2.如图8-22,用一个平面去截一个正方体,得到一个三棱锥。在这个三棱锥中,除截面外的三个面的面积分别为S1、S2、S3,则这个三棱锥的体积为( )
A.V=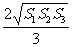 B.V=
B.V=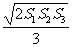
C.V=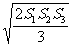 D.V=
D.V=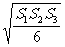
1.如果一个圆锥的侧面展开图恰是一个半圆,那么这个圆锥轴截面三角形的顶角为( )
A.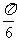 B.
B.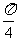 C.
C.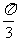 B.
B.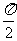
6.关于等积变换问题。
等积变换的依据是等底等高的棱锥体积相等。
等积变换求体积或求点到平面的距离,都是在基本几何体--四面体和平行六面体中进行的。这是因为这些几何体变换底面后,计算体积的方法不变,几何体仍为四面体和平行六面体,这样,我们就可以选择适当的面为底面,使计算简单、易行。
若几何体本身不是四面体或平行六面体,则需先将其分成几个四面体或平行六面体之后,再施行等积变换。
用等积变换求点到平面的距离,是用两种不同的体积计算方法,来建立所求距离的方程,使问题得解。
异面直线间的距离,可转化为点到平面的距离,因此也可用等积变换求解。
用等积变换求距离,可绕过距离的作图,从而降低了题目的难度。
[例题解析]
例1 如图8-1,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=30°,侧面A1ABB1是边长为a的菱形,且垂直于底面,∠A1AB=60°,E、F分别是AB1、BC的中点。
(1)求证:EF∥侧面A1ACC1;
(2)求四棱锥A--B1BCC1的体积;
(3)求EF与侧面A1ABB1所成角的大小。
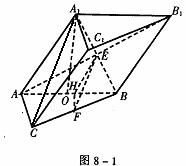
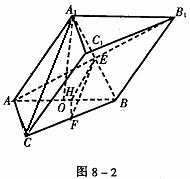
(1)连结A1B、A1C
∵A1ABB1是菱形,且E是AB1的中点,
∴E是A1B的中点。
又F是BC的中点,
∴EF∥A1C。
又A1C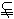 平面A1ACC1,
平面A1ACC1,
EF 平面A1ACC1,
平面A1ACC1,
∴EF∥面A1ACC1。
(2)∵平面A1ABB1⊥平面ABC,交线为AB,
∴在平面A1ABB1内,过A1作A1O⊥AB于O,则A1O⊥平面ABC,且h=A1O=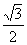 a,
a,
又∵AC⊥CB,∠ABC=30°,∴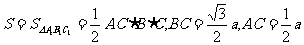 ,
,
∴V A-C CBB
CBB
=V柱-V A-A B
B C
C
=Sh - 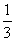 Sh=
Sh=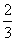 Sh=
Sh=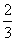 ·
·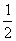 ·AC·BC·A1O
·AC·BC·A1O
=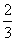 ·
·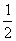 ·
·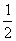 a·
a·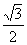 a·
a·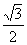 a =
a =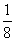 a3
a3
(3)在平面ABC内,过F作FH⊥AB于H,则FH⊥侧面A1ABB1。
连结EH,则∠HEF为EF与侧面A1ABB1所成的角。
∵在Rt△FHB中,FH=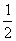 BF=
BF=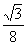 a,BH=
a,BH=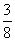 a;
a;
在△HEB中,HE=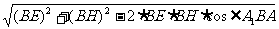
=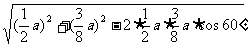
=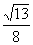 a,
a,
∴在Rt△EHF中,tan∠HEF=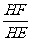 =
=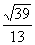 ,
,
∴∠HEF=arctan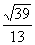 。
。
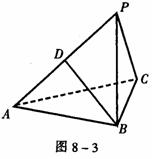
例2 如图8-3,三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB=2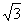 。
。
(1)求证:AC⊥BD;
(2)求BD与底面ABC所成的角(用反正弦表示);
(3)求三棱锥P-ABC的体积。
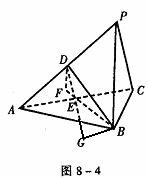
解 (1)如图8-4,取AC中点E,连DE、BE,则DE∥PC,∵PC⊥AC,∴DE⊥AC。
∵△ABC是正三角形,∴BE⊥AC。
又DE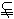 平面DEB,BE
平面DEB,BE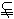 平面DEB,DE∩BE=E,∴AC⊥平面DEB。
平面DEB,DE∩BE=E,∴AC⊥平面DEB。
∵DB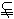 平面DEB,∴AC⊥DB。
平面DEB,∴AC⊥DB。
(2)法一:∵AC⊥平面DEB,AC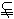 底面ABC,∴平面DEB⊥底面ABC,∴EB是DB在底面ABC内的射影,∠DBE是BD与底面ABC所成的角。
底面ABC,∴平面DEB⊥底面ABC,∴EB是DB在底面ABC内的射影,∠DBE是BD与底面ABC所成的角。
又∵DE⊥AC,BE⊥AC,∴∠DEB即为二面角P-AC-B的平面角。
在△DEB中,∵DE=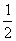 PC=1,BE=
PC=1,BE=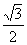 AB=3,
AB=3,
∴由余弦定理,得 BD2=12+32 –
2×1×3cos120°=13,BD=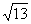 ,
,
∴由正弦定理,得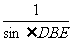 =
= ,
,
解得sin∠DBE=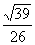 ,即BD与底面ABC所成的角为arcsin
,即BD与底面ABC所成的角为arcsin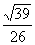 。
。
法二:∵AC⊥平面DEB,AC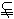 平面ABC。∴平面DEB⊥平面ABC,作DF⊥平面ABC,F为垂足,则F在BE的延长线上,∠DBF是BD与平面ABC所成的角。∵DE⊥AC,BE⊥AC,∴∠DEB是二面角P-AC-B的平面角。在Rt△DBF中,DE=
平面ABC。∴平面DEB⊥平面ABC,作DF⊥平面ABC,F为垂足,则F在BE的延长线上,∠DBF是BD与平面ABC所成的角。∵DE⊥AC,BE⊥AC,∴∠DEB是二面角P-AC-B的平面角。在Rt△DBF中,DE=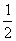 PC=1,BE=
PC=1,BE=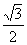 AB=3,
AB=3,
∠DEB=120°,∠DEF=60°,DF=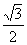 。
。
∴在△DEB中,由余弦定理得BD=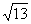 ,
,
∴sin∠DBF= =
=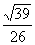 ,故BD与底面ABC所成的角为arcsin
,故BD与底面ABC所成的角为arcsin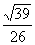 。
。
(3)∵AC⊥平面DEB,AC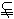 平面PAC,
平面PAC,
∴平面DEB⊥平面PAC,∴过点B作平面PAC的垂线段BG,垂足G在DE的延长线上。
∵在Rt△BEG中,∠BEG=60°,BE=3,∴BG= ,
,
∴VP-ABC=VB-PAC=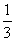 S△PAC×BG=
S△PAC×BG=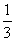 ×
×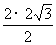 ×
× =3。
=3。
例3 如图8-5,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,PA、BC的公垂线DE=h,求三棱锥P-ABC的体积。
分析:思路一直接求三棱锥P-ABC的体积比较困难。考虑到DE是棱PA和BC的公垂线,可把原棱锥分割成两个三棱锥P-EBC和A-EBC,利用PA⊥截面EBC,且△EBC的面积易求,从而体积可求。
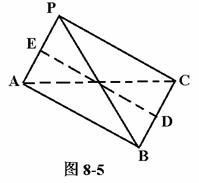
解 如图8-5-1,连结BE,CE。∵DE是PA、BC的公垂线,∴PA⊥DE。又PA⊥BC,∴PA⊥截面EBC。∴VP-EBC=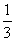 S△EBC·PE,VA-EBC=
S△EBC·PE,VA-EBC=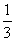 S△EBC·AE。∵DE⊥BC,∴S△EBC=
S△EBC·AE。∵DE⊥BC,∴S△EBC=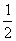 BC·DE=
BC·DE=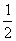 lh,∴VP-ABC=VP-EBC+VA-EBC=
lh,∴VP-ABC=VP-EBC+VA-EBC=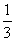 S△EBC·(PE+AE)=
S△EBC·(PE+AE)=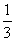 PA·S△EBC=
PA·S△EBC=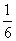 l2h。
l2h。
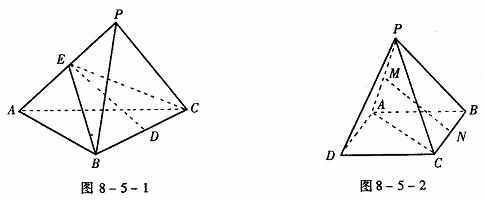
注 本例的解法称为分割法,把原三棱锥分割为两个三棱锥,它们有公共的底面△EBC,而高的和恰为PA,因而计算简便。
思路二 本题也可用补形法求解。
解 如图8-5-2,将△ABC补成平行四边形ABCD,连结PD,则PA⊥AD,且BC∥平面PAD,故C到平面PAD的距离即为BC和平面PAD的距离。
∵MN⊥PA,又MN⊥BC,BC∥AD,∴MN⊥AD, MN⊥平面PAD。
故 VP-ABC=VP-ADC=VC-PAD=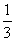 S△PAD·MN=
S△PAD·MN=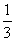 (
(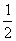 ·PA·AD)·MN=
·PA·AD)·MN=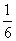 l2h。
l2h。
注 本题的解法称为补形法,将原三棱锥补形成四棱锥,利用体积互等的技巧进行转换,以达到求体积的目的。
本题也可将三棱锥补成三棱柱求积。想一想,怎样做?
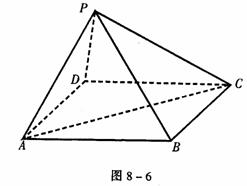
例4 如图8-6,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,并且PD=a, PA=PC=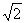 a。
a。
(1)求证:PD⊥平面ABCD;
(2)求异面直线PB与AC所成的角;
(3)求二面角A-PB-D的大小;
(4)在这个四棱锥中放入一个球,求球的最大半径。
解 (1)PC=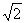 a,PD=DC=a,
a,PD=DC=a,
∴△PDC是Rt△,
且PD⊥DC。
同理,PD⊥AD。
而AD∩DC=D,∴PD⊥平面ABCD。
(2)如图8-7,连BD,∵ABCD是正方形,
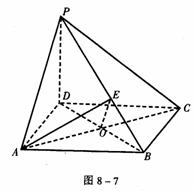
∴BD⊥AC。
又∵PD⊥平面ABCD。
∴BD是PB在平面ABCD上的射影。
由三垂线定理,得PB⊥AC。
∴PB与AC成90°角。
(3)设AC∩BD=O,作AE⊥PB于E,连OE。
∵AC⊥BD,又PD⊥平面ABCD,AC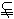 平面ABCD。
平面ABCD。
∴PD⊥AC。
而PD∩BD=D,∴AC⊥平面PDB,
则OE是AE在平面PDB上的射影。
由三垂线定理逆定理知OE⊥PB,
∴∠AEO是二面角A-PB-D的平面角。
∵PD⊥平面ABCD,DA⊥AB。∴PA⊥AB。
在Rt△PAB中,AE·PB=PA·AB。又AB= a
,AP=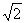 a,PB=
a,PB=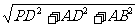 =
=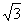 a,
a,
∴AE=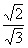 a。 又AO=
a。 又AO=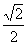 a
a
∴sin∠AEO=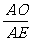 =
=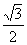 ,∠AEO=60°
,∠AEO=60°
∴二面角A-PB-D的大小为60°。
(4)设此球半径为R,最大的球应与四棱锥各个面相切,球心为S,连SA、SB、SC、SD、SP,则把此四棱锥分为五个小棱锥,它们的高均为R。
由体积关系,得
VP-ABCD=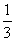 R(S△PDC+ S△PDA+ S△PBC+
S△PAB+ S正方形ABCD)
R(S△PDC+ S△PDA+ S△PBC+
S△PAB+ S正方形ABCD)
=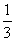 R(
R(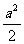 +
+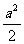 +
+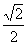 a2+
a2+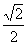 a2 + a2)。
a2 + a2)。
又∵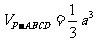 ,
,
∴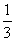 R(2a2+
R(2a2+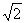 a2)=
a2)= 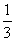 a3
a3
∴R=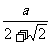 =
=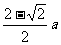 。
。
例5 如图8-8,已知长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心。求:
(1)二面角C-EB-O1的正切值;
(2)异面直线EB与O1F所成角的余弦值;
(3)三棱锥O1-BEF的体积。
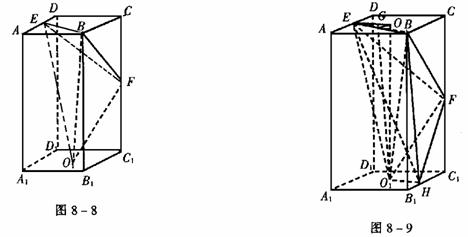
解 如图8-9,(1)取上底面的中心O, OG⊥EB于G,连OO1和GO1。由长方体的性质得OO1⊥平面ABCD,则由三垂线定理得O1G⊥EB,
则∠OGO1为二面角C-EB-O1的平面角。由已知可求得EB=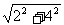 =2
=2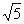 。
。
利用△ABE∽△GEO(图8-10),可求得OG=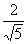 。
。
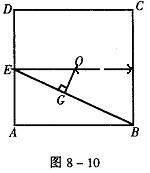
在Rt△O1OG中,tan∠O1GO=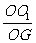 =4
=4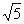 。
。
(2)在B1C1上取点H,使B1H=1,连O1H和FH。
易证明O1H∥EB,则∠FO1H为异面直线EB与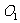 所成角。
所成角。
又O1H=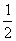 BE=
BE=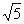 ,HF=
,HF=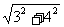 =5,
=5,
O1F=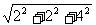 =2
=2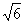 ,
,
∴在△O1HF中,由余弦定理,得
cos∠FO1H= =
=
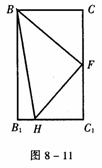
(3)连HB,HE,由O1H∥EB,得O1H∥平面BEF。
∴VO --BEF=VH-BEF=
VE-BHF=
--BEF=VH-BEF=
VE-BHF=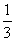 ·S△BHF·AB
·S△BHF·AB
∵S△BHF=32-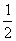 (1×8+3×4+4×4)=14
(1×8+3×4+4×4)=14
 --BEF=
--BEF=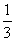 ×14×4=
×14×4=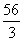
例6 如图8-12,球面上有四个点P、A、B、C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积。
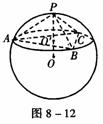
解 如图8-12,设过A、B、C三点的球的截面圆半径为r,圆心为O′,球心到该圆面的距离为d。在三棱锥P-ABC中,
∵PA,PB,PC两两互相垂直,且PA=PB=PC=a,
∴AB=BC=CA=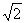 a,且P在△ABC内的射影即是△ABC的中心O′。
a,且P在△ABC内的射影即是△ABC的中心O′。
由正弦定理,得  =2r,∴r=
=2r,∴r=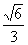 a。
a。
又根据球的截面的性质,有OO′⊥平面ABC,而PO′⊥平面ABC,
∴P、O、O′共线,球的半径R=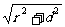 。又PO′=
。又PO′=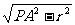 =
=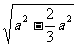 =
=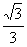 a,
a,
∴OO′=R - 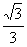 a=d=
a=d= ,(R-
,(R-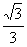 a)2=R2 – (
a)2=R2 – (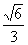 a)2,解得R=
a)2,解得R=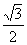 a,
a,
∴S球=4πR2=3πa2。
注 本题也可用补形法求解。将P-ABC补成一个正方体,由对称性可知,正方体内接于球,则球的直径就是正方体的对角线,易得球半径R=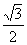 a,下略。
a,下略。
例7 如图8-13所示,四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC的中点,异面直线AD与BE所成的角为arccos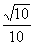 ,求四面体ABCD的体积。
,求四面体ABCD的体积。
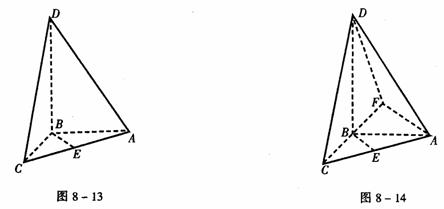
解 如图8-14,过A引BE的平行线,交CB的延长线于F,则∠DAF是异面直线BE与AD所成的角。
∴∠DAF=arccos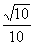
∵E是AC的中点,∴B是CF的中点,且BF=AB=2。∵AB⊥BC=2 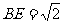
∴AF=2BE=2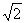
∴DF=DA,∵DB⊥BA,DB⊥BF,BF=BA,
则三角形ADF是等腰三角形,
AD=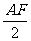 ·
· =
=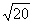 ,BD=
,BD= =4
=4
故四面体VABCD=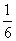 AB×BC×BD=
AB×BC×BD=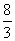 ,因此四面体ABCD的体积是
,因此四面体ABCD的体积是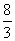 。
。
例8 如图8-15,在平行六面体ABCD-A1B1C1D1中,已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD=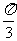 。
。
(1)求证:顶点A1在底面ABCD上的射影O在∠BAD的平分线上;
(2)求这个平行六面体的体积。
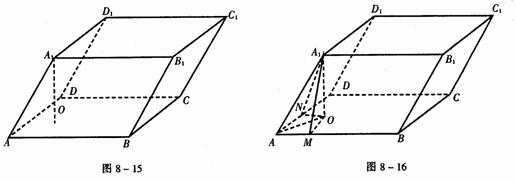
解 (1)如图8-16,连结A1O,则A1O⊥底面ABCD。作OM⊥AB交AB于M,作ON⊥AD交AD于N,连结A1M,A1N。由三垂线定得得A1M⊥AB,A1N⊥AD。∵∠A1AM=∠A1AN,
∴Rt△A1NA≌Rt△A1MA,∴A1M=A1N,
从而OM=ON。 ∴点O在∠BAD的平分线上。
(2)∵AM=AA1cos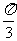 =3×
=3×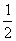 =
=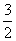
∴AO=AMsec =
=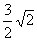 。又在Rt△AOA1中,
。又在Rt△AOA1中,
A1O2=AA12
– AO2=9 -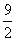 =
=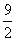 ,∴A1O=
,∴A1O=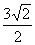 ,
,
∴平行六面体的体积V=5×4×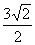 =30
=30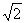 。
。
例9 如图8-17,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成角为45°,AB=a。
(1)求截面EAC的面积;
(2)求异面直线A1B1与AC之间的距离;
(3)求三棱锥B1-EAC的体积。
(1999年全国高考试题)
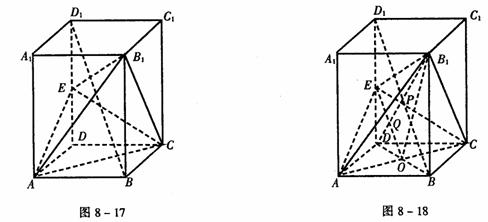
解 (1)如图8-18,连结DB交AC于O,连结EO。
∵底面ABCD是正方形,∴DO⊥AC。又∵ED⊥底面AC,∴EO⊥AC。∴∠EOD就是面EAC与底面AC所成的二面角的平面角,∠EOD=45°。
又DO=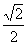 a, AC=
a, AC=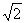 a, EO=
a, EO=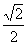 asec45°=a,故S△EAC=
asec45°=a,故S△EAC=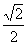 a2。
a2。
(2)由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,A1A⊥AC。又A1A⊥A1B1,∴A1A是异面直线A1B1与AC之间的公垂线。∵D1B∥面EAC,且面D1BD与面EAC交线为EO,∴D1B∥EO。又O是DB的中点,∴E是D1D的中点,D1B=2EO=2a。∴D1D=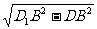 =
=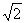 a,即异面直线A1B1与AC之间的距离为
a,即异面直线A1B1与AC之间的距离为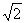 a。
a。
(3)法一:如图8-18,连结D1B,∵D1D=DB=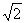 a,∴四边形BDD1B1是正方形。连结B1D交D1B于P,交EO于Q。∵B1D⊥D1B,EO∥D1B,∴B1D⊥EO。又AC⊥EO,AC⊥ED,∴AC⊥面BDD1B1,∴B1D⊥AC,∴B1D⊥面EAC。则B1Q是三棱锥B1-EAC的高。由DQ=PQ得B1Q=
a,∴四边形BDD1B1是正方形。连结B1D交D1B于P,交EO于Q。∵B1D⊥D1B,EO∥D1B,∴B1D⊥EO。又AC⊥EO,AC⊥ED,∴AC⊥面BDD1B1,∴B1D⊥AC,∴B1D⊥面EAC。则B1Q是三棱锥B1-EAC的高。由DQ=PQ得B1Q=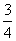 B1D=
B1D=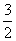 a,∴
a,∴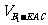 =
=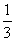 ·
·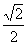 a 2·
a 2·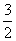 a =
a =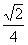 a 3。
a 3。
所以三棱锥B1-EAC的体积是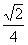 a 3。
a 3。
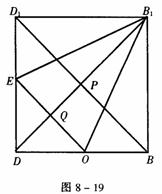
法二:连结B1O,则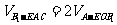 ∵AO⊥面BDD1B1,∴AO是三棱锥A-EOB1的高,且AO=
∵AO⊥面BDD1B1,∴AO是三棱锥A-EOB1的高,且AO=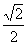 a。在正方形BDD1B1中,E、O分别是D1D、DB的中点(如图8-19),则
a。在正方形BDD1B1中,E、O分别是D1D、DB的中点(如图8-19),则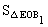 =
=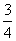 a2。
a2。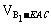 =2×
=2×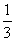 ×
×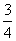 a 2×
a 2×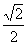 a=
a=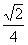 a 3。所以三棱锥B1-EAC的体积是
a 3。所以三棱锥B1-EAC的体积是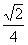 a 3。
a 3。
例10 如图8-20,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点。
(1)证明AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明面AED⊥面A1FD1;
(4)设AA1=2,求三棱锥F-A1ED1的体积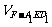 。
。
(1997年全国高考数学试题)
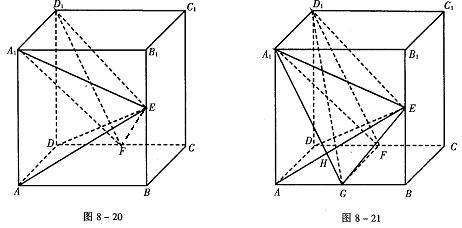
解 (1)∵多面体AC1是正方体,∴AD⊥面DC1。又D1F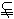 面DC1,∴AD⊥D1F。
面DC1,∴AD⊥D1F。
(2)如图8-21,取AB的中点G,连结A1G,FG。因为F是CD的中点,所以GF、AD平行且相等,又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F。设A1G与AE相交于点H,则∠AHA1是 AE与D1F所成的角。因为E是BB1的中点,所以Rt△A1AG≌Rt△ABE,∠GA1A=∠GAH,从而∠AHA1=90°,即直线AE与D1F所成角为直角。
(3)由(1)知AD⊥D1F,由(2)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED。又因为D1F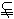 面A1FD1,所以面AED⊥面A1FD1。
面A1FD1,所以面AED⊥面A1FD1。
(4)连结EG,GD1,∵FG∥A1D1,∴FG∥面A1ED1,∴体积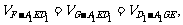
∵AA1=2,∴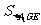 =
=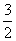 。∴
。∴ =
=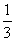 ×A1D1×
×A1D1×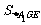 =
=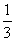 ×2×
×2×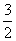 =1。
=1。
5.关于组合体体积的计算问题。
有很多的几何体,都由一些简单几何体所组成,这样的几何体叫做组合体。
构成组合体的方式一般有两种:其一是由几个简单几何体堆积而成,其体积就等于这几个简单几何体体积之和;其二是从一个简单几何体中挖去几个简单几何体而成,其体积就等于这个几何体的体积减去被挖去的几个几何体的体积。
因此,组合体体积的求法,即为“加、减”法,关键是合理的分割,可使计算简化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com