
6.
解析1)金属棒开始下滑的初速为零,由牛顿第二定律,有
mgsinθ-μmgcosθ=ma (2分)
a=4 m/s2 (2分)
(2)设金属棒运动达到稳定时,速度为v、所受安培力为F,棒在沿导轨方向受力平衡mgsinθ-μmgcosθ-F=0 (2分)
此时金属棒克服安培力做功的功率等于电路中电阻消耗的功率
Fv=P
有v=10 m/s (2分)
(3)设电路中电流为I,两导轨间金属棒长为L,磁感应强度为B
则I=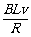 (2分)
(2分)
P=I2R
∴B=0.4 T,方向垂直导轨平面向上 (2分)
5.

4.

3.
解析(1)因a、b在磁场中匀速运动,由能量关系知
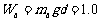 J
(3分)
J
(3分)
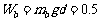 J
(3分)
J
(3分)
(2)b在磁场中匀速运动时:速度为vb,总电阻R1=7.5 Ω
b中的电流Ib=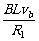 ①
①
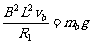 ②
②
同理,a棒在磁场中匀速运动时:速度为va,总电阻R2=5 Ω:
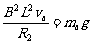 ③
③
由以上各式得: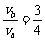 ④(4分)
④(4分)
(3)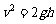 ⑤
⑤
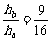 ⑥
⑥
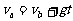 ⑦
⑦
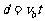 ⑧
⑧
由④⑤⑥⑦⑧得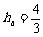 m=1.33 m
m=1.33 m 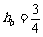 m=0.75
m
(4分)
m=0.75
m
(4分)
2.
解:(1)设金属杆a滑至水平轨道时速率为v1
由机械能守恒,有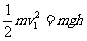 (1分)
(1分)
得: (1分)
(1分)
a进入水平轨道后,发生电磁感应,产生感应电流,使金属杆a、b受到等大反向的安培力,由分析可知,金属杆a、b最终将以相同的速率v2向右运动,把金属杆a、b视为系统,由动量守恒有: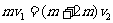 (1分)
(1分)
解得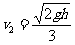 (1分)
(1分)
(2)当金属杆a的速度变为原来的一半,即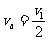 时,设b的速度为vb,由动量守恒,有:
时,设b的速度为vb,由动量守恒,有: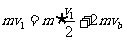 (2分)
(2分)
a棒产生的感应电动势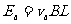 (1分),b棒产生的感应电动势
(1分),b棒产生的感应电动势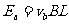 (1分),
(1分),
两电动势方向相反,所以回路总电动势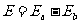 (1分)
(1分)
流过a棒的电流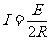 (1分)
(1分)
a棒所受安培力为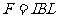 (1分)
(1分)
a棒的加速度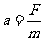 (1分)
(1分)
以上各式联立解得: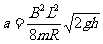 (2分)
(2分)
1.
解:(1) 金属棒在上升的过程,切割磁感线产生的感应电动势为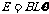 ,
,
回路的总电阻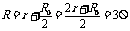 (1分),回路中的感应电流
(1分),回路中的感应电流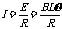
金属棒受到平行于导轨向下的安培力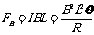 (2分)
(2分)
金属棒还受到平行于导轨向下的力有mgsinθ、滑动摩擦力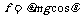
由牛顿运动定律可知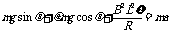 (2分)
(2分)
金属棒上升过程中的最大加速度对应的是金属棒的最大速度,金属棒上升过程做减速运动,所以金属棒上升过程中的最大加速度就是速度为υ0的瞬间
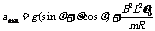
代入数据后得最大加速度amax=10.3m/s2(2分)
(2)金属棒上升到最高点的过程中,通过上端电阻的电量Δq=0.1C,即金属棒中通过的电量为2Δq,设金属棒中的平均电流为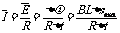 通过金属棒的电量
通过金属棒的电量
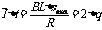 (2分)
(2分)
金属棒沿导轨上升的最大距离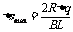 代入数据后得
代入数据后得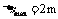 (1分)
(1分)
上端电阻与下端电阻相等,并联后电阻为1Ω,再与金属棒的电阻r=2Ω串联,外电路是产生的焦耳热为全电路焦耳热的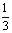 ,上端电阻的焦耳热Q又为外电路焦耳热的
,上端电阻的焦耳热Q又为外电路焦耳热的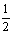 ,全电路产生的焦耳热为6Q.由能量守恒可知
,全电路产生的焦耳热为6Q.由能量守恒可知
 (2分)
(2分)
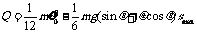
代入数据后得Q=5J(2分)
11.B 12.B 13.BC 14.D
1.D 2.A 3.B 4.AD 5.D 6.AC 7.A 8.D 9.BCD 10.AD
3.(二校联考) 如图所示,电阻忽略不计的、两根平行的光滑金属导轨竖直放置,其上端接一阻值为3 Ω的定值电阻R. 在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B、磁场区域的高度为d=0.5 m. 导体棒a的质量ma-0.2 kg,电阻Ra=3 Ω;导体棒b的质量mb=0.l 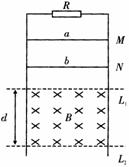 kg,电阻Rb=6 Ω.它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当b刚穿出磁场时a正好进入磁场. 设重力加速度为g=l0
m/s2. (不计a、b之间的作用,整个运动过程中a、b棒始终与金属导轨接触良好)求:
kg,电阻Rb=6 Ω.它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当b刚穿出磁场时a正好进入磁场. 设重力加速度为g=l0
m/s2. (不计a、b之间的作用,整个运动过程中a、b棒始终与金属导轨接触良好)求:
(1)在整个过程中,a、b两棒克服安培力分别做的功;
(2)a进入磁场的速度与b进入磁场的速度之比;
(3)分别求出M点和N点距L1的高度.
(湖师大附中6)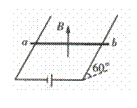 4.如图所示,在与水平方向成60°角的光滑金属导轨间连一电源,在相距 lm的平行导轨上放一重为3N的金属棒
4.如图所示,在与水平方向成60°角的光滑金属导轨间连一电源,在相距 lm的平行导轨上放一重为3N的金属棒 ,棒上通过3A的电流,磁场
,棒上通过3A的电流,磁场
方向竖直向上,这时棒恰好静止,求:
(1)匀强磁场’,嵫感应强度;
(2) 棒对导轨的压力;
棒对导轨的压力;
(3)若要使B取值最小,其方向应如何调整?并求出最小值.
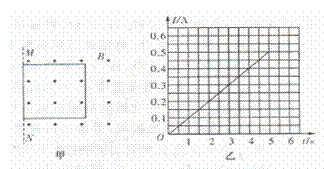 (湖师大附中6)5. 如图甲所示,边长为L=2.5m、质M=0.50kg的正方形金属线框放在磁感应强度B=0.80T的匀强磁场中.它的一边与磁场的边界N重合,在力F的作用下由静止开始向左运动,测得金属框中的电流随时间变化的图象如图乙所示.已知金属线框的总电阻R=4.0
(湖师大附中6)5. 如图甲所示,边长为L=2.5m、质M=0.50kg的正方形金属线框放在磁感应强度B=0.80T的匀强磁场中.它的一边与磁场的边界N重合,在力F的作用下由静止开始向左运动,测得金属框中的电流随时间变化的图象如图乙所示.已知金属线框的总电阻R=4.0 .
.
(1)试判断_金属线框从磁场中拉出的过程中,线框中感应电流的方向;
(2)求t=2.0s时金属线框的速度和力F的大小;
(3)已知在5.0s内,力F做功1.92J.求5.0s内,线框产生的热量.

(湖师大附中5)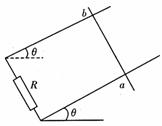 6.如图,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1 m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻,匀强磁场方向与导轨平面垂直,质量为0.2 kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
6.如图,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1 m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻,匀强磁场方向与导轨平面垂直,质量为0.2 kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8 W,求该速度的大小;
(3)在上问中,若R=2 Ω,金属棒中的电流方向由a→b,求磁感应强度的大小和方向.(g=10 m/s2,sin37°=0.6,cos37°=0.8)
 (岳阳一中)7.如图10甲所示,空间存在B=0.5T、方向竖直向下的匀强磁场,MN、PQ是放在同一水平面内的粗糙平行长直导轨,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,对ab施加一个大小为F=0.45N,方向水平向左的恒定拉力,使其从静止开始沿导轨运动,此过程中棒始终保持与导轨垂直且良好接触,图乙是棒的运动速度――时间图象,其中AO是图象坐标原点0点时刻的切线(切线的斜率即为棒在0时刻的加速度),AB是图象的渐近线,除R外其余部分的电阻不计。
(岳阳一中)7.如图10甲所示,空间存在B=0.5T、方向竖直向下的匀强磁场,MN、PQ是放在同一水平面内的粗糙平行长直导轨,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,对ab施加一个大小为F=0.45N,方向水平向左的恒定拉力,使其从静止开始沿导轨运动,此过程中棒始终保持与导轨垂直且良好接触,图乙是棒的运动速度――时间图象,其中AO是图象坐标原点0点时刻的切线(切线的斜率即为棒在0时刻的加速度),AB是图象的渐近线,除R外其余部分的电阻不计。
⑴求R的阻值。
⑵当棒的位移为100m时,其速度已经达到10m/s,
求此过程中电阻上产生的热量。
湖南省2009届高三物理模拟试题专题精编
2.(长沙一中)如图所示,两根金属轨道之间的距离为L,轨道水平部分有竖直向上的匀强磁场B,一质量为m的金属杆a在离地h的高处从静止开始沿弧形轨道下滑,一根质量为2m的金属杆b原来静止放置在水平轨道上,水平轨道足够长,设金属杆a、b不会相碰,金属杆a、b的电阻都是R,其它电阻不计,不计任何摩擦,求: .
. .
.
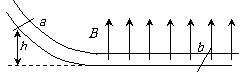 (1)a和b的最终速度是多大?
(1)a和b的最终速度是多大? .
. .
.
(2)当a的速度变为进入磁场时的一半时,a的加速度是多大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com