19、(本题满分12分)

如图，在四棱锥S-ABCD中，底面ABCD是边长为1的菱形，，

SA=2，M为SA上的中点，N在线段BC上。

(I)当为何值时，MN//平面SCD(说明理由)；

(II)求MD和平面SCD所成角的正弦值。

18、(12分)设函数．

(1)求函数的最小正周期和单调递增区间；

(2)当时，的最大值为2，求的值，并求出的对称轴方程．

17、(12分)不等式选讲：

求|2x-3|+|3x+2|的最小值。

16、如图所示，圆O的直径AB＝6，C为圆周上一点，BC＝3，过C作圆的切线，则点A到直线的距离AD为　　　　 .

15、已知点满足条件

的最大值为8，　 则　　　 .

14、设点P、Q、R是线段AB的四等分点，则有　　　　 　

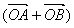
13、=　　　　　　 。

12、对于函数f(x)=e^x,定义域中任意x₁,x₂(x₁≠x₂)有如下结论：

①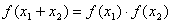　 ②

③　　　　　 ④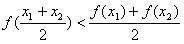

上述结论中正确的结论个数是……………………………………………………………(　　 )

A．1　　　　　　 　　 B．2　　　　　 　　 　　C．3　　　 　　　 　 D．4

第Ⅱ卷(非选择题　 共90分)

11、下图是2009年举行的某次民族运动会上，七位评委为某民族舞蹈打出的分数的茎叶统

计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为……………(　　 )

A．，　　　 B．，　　 C．，　　　 D．，　

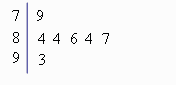
10、设奇函数在上为增函数，且，则不等式的解集为…………………………………………………………………………………………(　　 )

A．　　　　　　　　 　　　 B．

C．　　　　　　 　　　 D．