1.三角函数恒等变形的基本策略。

(1)常值代换：特别是用“1”的代换，如1=cos²θ+sin²θ=tanx·cotx=tan45°等。

(2)项的分拆与角的配凑。如分拆项：sin²x+2cos²x=(sin²x+cos²x)+cos²x=1+cos²x；配凑角：α=(α+β)－β，β=－等。

(3)降次与升次。即倍角公式降次与半角公式升次。

(4)化弦(切)法。将三角函数利用同角三角函数基本关系化成弦(切)。

(5)引入辅助角。asinθ+bcosθ=sin(θ+)，这里辅助角所在象限由a、b的符号确定，角的值由tan=确定。

(6)万能代换法。巧用万能公式可将三角函数化成tan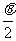的有理式。

10.反三角函数中的关系式

(1)arcsin(－x)=－arcsinx

(2)arccos(－x)= π－arccosx

(3)arctan(－x)=－arctanx

(4)arccot(－x)=π－arccotx

(5)arcsinx+arccosx=

(6)arctanx+arccotx=

9.三角形中的公式

(1)正弦定理： ===2R

(2)余弦定理：a²+b²－c²=2abcosC

b²+c²－a²=2bccosA

c²+a²－b²=2cacosB

正弦定理、余弦定理沟通了角与边的关系，可使边转化为角，也可使角化为边。

(3)三角形的面积公式，设△ABC的面积为△，则

△=ab·sinC=bc·sinA=ac·sinB

=2R²sinA·sinB·sinC=

==p·r

其中p为△ABC周长的一半，即p=(a+b+c),R与r分别为△ABC的外接圆与内切圆的半径。

(4)若在△ABC中，三边a、b、c成等差数列，则有下列结论：

①a+c=2b

②sinA+sinC=2sinB

③cos=2cos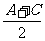

(4)tan·tan=

(5)0<B≤

(6)cot,cot,cot成等差数列。

8.在△ABC中常用的恒等式

(1)tanA+tanB+tanC=tanA·tanB·tanC

(2)cotA·cotB+cotB·cotC+cotC·cotA=1

(3)tantan+tantan+tantan=1

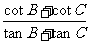(4)++=1

(5)sinA+sinB+sinC=4coscoscos

(6)cosA+cosB+cosC=1+4sinsinsin

7.常用的三角恒等式

(1)sin²α－sin²β=sin(α+β)sin(α－β)

(2)cos²α－cos²β=sin(β－α)sin(β+α)

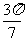(3)cos+cos+cos=

(4)sin3α=3sinα－4sin³α

(5)cos3α=4cos³α－3cosα

(6)sin²(α+β)=cos²α+cos²β－2cosαcosβ·cos(α+β)

(7)sinα+sin(α+π)+sin(α+)=0

(8)sin²α+sin² (α+π)+sin² (α+)=

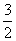
(9)sin³α+sin³ (α+π)+sin³ (α+)= －sin3α

(10)cos³α+cos³ (α+π)+cos³ (α+)=cos3α

(11)sin⁶α+cos⁶α=+cos4α

(12)sin(α－β)·sin(δ－γ)+sin(β－γ)·sin(δ－θ)+sin(γ－α) ·sin(δ－β)=0

(13)sinα+sinβ+sinγ－sin(α+β+γ)

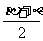　 =4sin·sin·sin

(14)cosα+cosβ+cosγ+cos(α+β+γ)

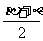　 =4cos·cos·cos

(15)tanα·tan2α+tan2α·tan3α+…+tan(n－1)αtannα=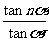－n

6.三角函数公式内在联系

5.函数图像变换理论

(1)函数y=f(－x)的图像与函数y=f(x)的图像关于y轴对称；

(2)函数y=－f(x)的图像与函数y=f(x)的图像关于x轴对称；

(3)函数x=f(y)的图像与函数y=f(x)的图像关于直线y=x对称；

(4)函数x=－f(－y)的图像与函数y=f(x)的图像关于直线y=－x对称；

(5)函数y=－f(－x)的图像与函数y=f(x)的图像关于原点(0，0)对称；

(6)函数y=f(x+p)(p>0)的图像是将函数y=f(x)的图像向左平移p个单位而得；

(7)函数y=f(x－p)(p>0)的图像是将函数y=f(x)的图像向右平移p个单位而得；

(8)函数y=f(x)+q的图像是将函数y=f(x)的图像向上或向下平移|q|个单位而得，当q>0时，向上，q<0时向下；

(9)函数y=f(px)(p>0)的图像是将函数y=f(x)的图像上各点的横坐标变为原来的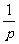(纵坐标不变)；

(10)函数qy=f(x)(q>0)即y=f(x)的图像是将函数y=f(x)的图像上各点的纵坐标变为原来的(横坐标不变)。

4.函数y= Asin(ωx+)(A，ω>0)的性质

(1)定义域是R；

(2)值域[－A，A]；

(3)单调区间：在区间[，](k∈Z)上是增函数；在区间[，](k∈Z)上是减函数；

(4)奇偶性：当=kπ+时是偶函数，当=kπ时是奇函数，当≠时是非奇非偶函数(k∈Z)；

(5)周期性：是周期函数且最小正周期为T=；

(6)对称性：关于点(，0)中心对称，关于直线x=轴对称。

3.三角函数线

三角函数线是通过有向线段直观地表示出角的各种三角函数值的一种图示方法。利用三角函数线在解决比较三角函数值大小、解三角方程及三角不等式等问题时，十分方便。

2.终边相同的角、区间角与象限角

(1)终边相同的角是指与某个角α具有同终边的所有角，它们彼此相差2kπ(k∈Z)，即β∈{β|β=2kπ+α，k∈Z}，根据三角函数的定义，终边相同的角的各种三角函数值都相等。

(2)区间角是介于两个角之间的所有角，如α∈{α|≤α≤}=[，]。

(3)象限角，α的终边落在第几象限，就称α是第几象限角。

(4)α、、2α之间的关系。若α终边在第一象限则终边在第一或第三象限；2α终边在第一或第二象限或y轴正半轴。

若α终边在第二象限则终边在第一或第三象限；2α终边在第三或第四象限或y轴负半轴。

若α终边在第三象限则终边在第二或第四象限；2α终边在第一或第二象限或y轴正半轴。

若α终边在第四象限则终边在第二或第四象限；2α终边在第三或第四象限或y轴负半轴。