
1.史书记载“水激轮转,众筒兜水,次第下倾于岸上,以灌稻田,日夜不息,绝胜人力。”这种利用水力的灌溉工具是 ( )
A.水排 B.耧车 C.翻车 D.筒车
 2.中
国古代君主有颁布《罪己诏》的传统。其内容一般是君主反省自己的德行和政策。唐德宗曾颁《罪己大赦诏》曰:“天谴于上而朕不悟,人怨于下而朕不知”。与上述思想有关的派别是 ( )
2.中
国古代君主有颁布《罪己诏》的传统。其内容一般是君主反省自己的德行和政策。唐德宗曾颁《罪己大赦诏》曰:“天谴于上而朕不悟,人怨于下而朕不知”。与上述思想有关的派别是 ( )
A.儒家 B.道家
C.法家 D.墨家
22.(本题满分15分)
已知函数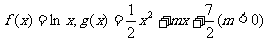 ,
,
(I)若直线l与函数 的图象都相切,且与函数
的图象都相切,且与函数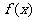 的图像的切点的横坐标为1,求直线l的方程及m的值;
的图像的切点的横坐标为1,求直线l的方程及m的值;
(II)若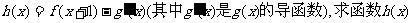 的最大值;
的最大值;
(III)当
21.(本题满分15分)
如图△ABC为直角三角形, 点M在y轴上,且
点M在y轴上,且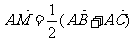 ,点C在x轴上移动,
,点C在x轴上移动,
(I)求点B的轨迹E的方程;
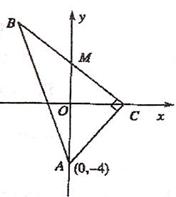
(II)过点 的直线l与曲线E交于P、Q两点,设
的直线l与曲线E交于P、Q两点,设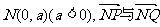 的夹角为
的夹角为 的取值范围;
的取值范围;
 (III)设以点N(0,m)为圆心,以
(III)设以点N(0,m)为圆心,以 为半径的圆与曲线E在第一象限的交点H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求实数m的值。
为半径的圆与曲线E在第一象限的交点H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求实数m的值。
20.(本题满分14分)
有10张形状大小完全相同的卡片,其中2张写着数字0,另外5张写着数字1,余下3张上写着数字2。从中随机取出1张,记下它的数字后原样放回,重复取2次,记ξ为2次数字之和。
(I)求概率 ;
;
(II)求随机变量ξ的分布列及数学期望。
19.(本题满分14分)
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD//BC//EF,AB⊥AD,M为EC的中点,AF=AB=BC=FE= AD。
AD。
(I)求异面直线BF与DE所成的角的大小;
 (II)证明平面AMD
(II)证明平面AMD 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
18.(本题满分14分)
设函数
(I)求函数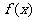 的最小正周期及函数的单调递增区间 ;
的最小正周期及函数的单调递增区间 ;
(II)若 ,是否存在实数m,使函数
,是否存在实数m,使函数 ?若存在,请求出m的取值;若不存在,请说明理由。
?若存在,请求出m的取值;若不存在,请说明理由。
16.使不等式 都成立的最小正整数
都成立的最小正整数 的值为
。
的值为
。
 17.如图,平面
17.如图,平面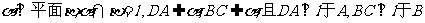 ,AD=4,BC=8,AB=6,在平面
,AD=4,BC=8,AB=6,在平面 上的动点P,记PD与
上的动点P,记PD与
平面 所成角为
所成角为 ,PC与平面
,PC与平面 ,若
,若 ,
,
则△PAB的面积的最大值是 。
15.将数字1,2,3,4,5,6按第一行1个数,第二行2个数,第三行3个数的形式随机排列,设 行中最大的数,则满足
行中最大的数,则满足 的所有排列的个数是 。(用数字作答)
的所有排列的个数是 。(用数字作答)
14.已知钝角三角形ABC的最大边长为4,其余两边长分
别为x,y,那么以 为坐标的点所表示的平面区
为坐标的点所表示的平面区
域的面积是 。
13.已知 展开式中常数项为1120,
展开式中常数项为1120,
则此展开式中各项系数的和等于 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com