
5. 深圳市农科集团第二次在全市范围内公开征集的包括紫叶生菜、孔雀草等多种生物育种材料随“神舟飞船”在大空邀游110多个小时后返回地面,由此该集团又确立了一批太空农业项目。下列有关生物技术及原理,说法正确的是
A.返回地面后,孔雀草开出不常见的墨色花,其根本原因最可能是发生了基因重组
B.如果在孔雀草的种植过程中发现开出了不常见的墨色花时,为了快速大量生产,宜采用植物组织培养技术
C.在培育转基因抗虫孔雀草时,获取目的基因用的工具酶有限制酶、DNA连接酶和运载体
D.在太空环境条件(失重、强辐射等)下,孔雀草种子不可能发芽
4. Ⅰ.某植物块根的颜色由两对自由组合的基因共同决定。只要基因R存在,块根必为红色,rrYY或rrYy为黄色,rryy为白色;在基因M存在时果实为复果型,mm为单果型。现要获得白色块根、单果型的三倍体种子。
(1)请写出以二倍体黄色块根、复果型(rrYyMm)植株为原始材料,用杂交育种的方法得到白色块根、单果型三倍体种子的主要步骤。
①
②
③
④
(2)如果原始材料为二倍体红色块根、复果型的植株,你是否一定能通过杂交育种的方法获得白色块根、单果型的三倍体种子?
II.芽的分生组织细胞发生变异后,可表现为所长成的枝条和植株性状改变,称为芽变。
(1)为确定某果树枝条的芽变是否与染色体数目变异有关,可用 _______________ 观察正常枝条与芽变枝条的染色体数目差异。
(2)桃树可发生芽变。已知桃树株型的高株(D)对矮株(d)为显性,果型的圆(A)对扁(a)为显性,果皮毛的有毛(H)对无毛(h)为显性,现从高株圆果有毛的桃树(DdAaHh)中,选到一株高株圆果无毛的芽变个体(这一芽变是由一对等位基因中一个基因突变造成的)。在不考虑再发生其他突变的情况下,未芽变桃树(DdAaHh)测交后代发生分离的性状有 _______________ ,原因是_______________;芽变桃树测交后代发生分离的性状有 _______________ ,原因是 _______________。
(3)上述桃树芽变个体用枝条繁殖,所得植株群体性状表现型为 _______________ 请用细胞分裂的知识解释原因 ___________________________ 。
3.江西省农科院水稻研究所专家成功培育出一种名为 “傻瓜水稻”的新品种。这种新品种类似于韭菜,割完后的稻在第二二年还能再生长,并能收获种子。右图是“傻瓜水稻”产生图。(野生稻是于1978年在江西省东乡县发现的,是多年生草本植物,能在自然条件下越冬)。请据图分析并回答:

(1)完成过程①②所依据的遗传学原理是_______ 。
(2)割完后的稻茬第二年还能再生长,并能收获种子,这种生殖方式的意义是_________________ 。
II.人的耳垢有油性和干性两种,是受单基因(A、a)控制的。有人对某一社区的家庭进行了调查,结果如下表:
|
组合序号 |
双亲性状 |
家庭数日 |
油耳男孩 |
油耳女孩 |
干耳男孩 |
干耳女孩 |
|
一 |
♂油耳×油耳♀ |
195 |
90 |
80 |
10 |
15 |
|
二 |
♂油耳×干耳♀ |
80 |
25 |
30 |
15 |
10 |
|
三 |
♂干耳×油耳♀ |
60 |
26 |
24 |
6 |
4 |
|
四 |
♂干耳×干耳♀ |
335 |
0 |
0 |
160 |
175 |
|
合计 |
670 |
141 |
134 |
191 |
204 |
(1)控制该相对性状的基因位于___________ 染色体上,判断的依据是 _________。
(2)一对油耳夫妇生了一个千耳儿子,推测母亲的基因型是____________,这对夫妇生一个油耳女儿的概率是__________。
(3)从组合一的数据看,子代性状没有呈典型的孟德尔分离比(3∶1),其原因是 _______。
(4)若一对干耳夫妇生了一个左耳是干性的、右耳是油性的男孩,出现这种情况的原因可能是_____________。
2. 用生长素处理获得无籽番茄和用多倍体育种获得无籽西瓜, 下列有关的叙述正确的是 ( )
A.生长素处理获得番茄无籽的变异属于不能遗传的变异
B.无籽番茄植株扦插后长出的植株仍结无籽果实
C.三倍体西瓜无籽的变异属于不能遗传的变异
D.无籽番茄属于单倍体植物
1.下列关于育种原理的几种说法,不正确的是 ( )
A.育种的过程是一个选择的过程,选择方向与自然选择有所不同
B.育种的过程是一个选择的过程,选择方向与自然选择相同
C.能够创造出新品种甚至新类型的重要方法是诱变
D.育种是对变异人工进行定向选择的过程
(二)几种育种方案的比较
(一) 遗传育种是历年高考考查的重点。该部分内容在高考中的主要考点有:
1、杂交育种和诱变育种的优点和局限性
2、遗传和变异规律在改良农作物和培育家畜品种等方面的应用
3、重组DNA技术(又叫基因工程)
4、关注转基因生物和转基因食品的安全性
(二)、
|
育种方式 |
例子 |
原理 |
特点 |
|
诱变育种 |
利用一定剂量的射线处理水稻种子,培育出成熟期提早15天的品种 |
在一定条件下,DNA复制时发生差错,使碱基对的排列顺序发生局部的改变(即基因突变) |
优点:a能加快育种的进程(可以提高变异的频率使后代的变异性状比较快地稳定) b大幅度地改良某些性状。 缺点:诱发产生的突变,有利的个体不多 |
|
杂交育种 |
高秆抗锈病和矮秆易染病的纯种小麦杂交得到F1,Fl自交后在F2中得到矮秆抗锈病的品种。再经过选择培育即可得到符合生产要求的新品种 |
在生物体有性生殖的过程中控制不同性状的基因可以重新组合(即基因重组) |
优点:使两个亲本的优良性状结合在一起 缺点:需要较长时间 |
|
单倍体育种 |
高秆抗锈病和矮秆易染病的纯种小麦杂交得到F1,将F1的花粉离体培养,再用秋水仙素处理它的幼苗,诱导染色体数目加倍从而得到矮秆抗锈病的纯种 |
先采用花药的离体培养的方法获得单倍体,再经人工诱导使它的染色体数目加倍,这样培育出的新植株不仅含有体细胞的染色体数,而且 每对染色体上的成对基因都是纯合的 |
育种年限较短(培育出的植株自交后产生的后代不会发生性状分离) |
|
多倍体育种 |
我国育种专家鲍文奎利用小麦和黑麦杂交得到高度不育的F1(四倍体),再用秋水仙素处理,最终培育出抗寒耐瘠、优质高产的小黑麦(八倍体) |
秋水仙素处理后的细胞在有丝分裂时虽然染色体能复制但纺锤体的形成被抑制,不能形成两个子细胞,从而使细胞的染色体加倍 |
优点:糖分和蛋白质等营养物质含量高 缺点:发育延迟,结实率相对较低 |
|
基因工程育种 |
转基因作物(抗虫棉) |
基因重组 |
打破了物种界限.定向改变生物性状 |
|
细胞工程育种 |
白菜-甘蓝 |
细胞融合 |
打破物种界限 |

(一)、
浅谈基因工程在玉米遗传育种中的应用
育种工作者都希望培育出性状优良的品种,而实现这一目标的关键是得到目的基因和对高产、优质、抗病虫等目标性状的选择。过去人们多借用形态学和同工酶等遗传标记来辅助育种,并已在玉米育种中获得了成功。但由于受环境等因素影响,这些方法要求经验丰富的育种者花费较长的时间。近年来,基因工程在玉米遗传育种中取得了巨大进展。基因工程弥补了玉米遗传资源的不足.并解决了过去不能解决的难题。
1基因工程在玉米遗传育种中的应用现状
1.1基因工程的进展及应用概况
20世纪80年代初,RFLP作为遗传标记构建人类遗传连锁图首次使用,随后各种分子标记技术发展迅速.并在动、植物遗传的研究中得以广泛应用。1983年第一个转基因植物问世,随后基因工程发展日新月异。迄今为止.全世界已分离目的基因100多个,获得转基因植物近200种,有的已进入或正在进入商业开发阶段,植物基因工程对高科技农业发展的重要性举世瞩目。基因工程集现代新技术为一体,如DNA重组技术、分子杂交技术、细胞培养技术、基因转化技术和基因表达调控技术等,使育种途径进入了一个高新技术时代。1988年以前,玉米组织培养只能用愈伤组织再生植株,原生质体再分化植株没有成功。直到1993年,玉米基因工程研究才取得了一系列成绩。在玉米遗传育种中常用的基因工程技术主要有分子标记、DNA重组技术(也称转基因技术)等。转基因技术方法主要有农杆菌、基因枪、PEG介导等方法,到目前为止,在玉米基因工程中应用最多,效果最好的转基因方法就是基因枪法。分子标记自1980年以来发展迅速。多种DNA分子标记技术的应用,解决了许多玉米遗传育种工程技术上的难题。转基因技术、分子标记技术等基因工程技术被广泛应用于玉米自交系的遗传多样性分析,玉米优势群划分,玉米雄性不育系的研究.玉米品质改良,玉米病虫害抗性等方面。
1.2基因转化技术在玉米遗传育种中的应用
玉米转基因技术应用领域十分广泛,主要应用在抗除草剂玉米、特种玉米等方面。抗虫转基因玉米主要应用的是苏云金杆菌分离苏云金杆菌杀虫结晶蛋白基因(简称Bt基因)和从植物中分离出的昆虫蛋白酶抑制基因(广泛应用的是豆胰蛋白酶抑制剂基因CpTL及植物凝集素基因等。目前所发现的Bt基因.可以毒杀鳞翅目、双翅目、鞘翅目的昆虫。CpTL对于许多给农业生产造成重大经济损失的害虫都具有抗性,其中包括玉米螟、鞘翅目的玉米根叶甲、杂拟谷盗、直翅目的蝗虫等。将抗除草剂耐性引入玉米是增加除草剂选择及安全性的一种新途径,BASF公司开发的抗除草剂玉米对于稀禾定具有高度耐受性,使其可以在玉米发芽后喷施,防止所有的禾本科杂草。美国得克萨斯大学试验站的ProdiGene公司把遗传工程玉米天然产生的特别蛋白推向市场。抗冻蛋白(AFP)是具有降低冰点和减少冰晶生长速度的蛋白质.通过电激法人工合成的黄盖鲽AFP基因被导入玉米原生质中并获得了表达。近年来.转基因玉米层出不穷。1998年,转基因玉米占全球转基因作物面积的30%.仅次于转基因大豆.主要是抗虫玉米和耐除草剂玉米。



Mcumullen(1995)等报道抗玉米矮花叶病毒基因mdml被定位于6号染色体短臂上。大量研究表明。玉米抗病虫基因在染色体上聚群存在,这有利于提高抗病基因的克隆效率。利用玉米抗性基因群可以在有抗病基因存在的染色体区段构建高密度的遗传连锁图谱。这种图谱可以用来克隆目标基因。总之,随着大量抗病基因分子标记的不断发掘及精确定位,标记辅助选择必将在常规抗病育种中发挥愈来愈重要的作用。随着分子生物学的发展,一大部分控制重要性状的基因相继被定位到饱和的分子标记图谱上.可利用图谱分离和克隆这些基因,最终用基因工程手段来改良品种。此外,DNA分子标记技术,还用来进行种性和种子质量鉴定,这也为品种知识产权保护和种子质量监测提供了可靠依据。
1.3分子标记技术在玉米遗传育种中的应用
随着分子生物学的发展,开发了一类基于DNA变异的分子标记。目前,已开发了多种分子标记,主要有:限制性片段长度多态性(RFLP)、随机扩增多态DNA(RAPD)、扩增片段长度多态性(AFLP)、简单序列重复(SSR)、序列特异扩增区域(SCAR)、单链构象多态性(SSCP)、单核苷酸多态性(SNP)和数量可变串联重复(VNTR)等。分子标记直接以DNA形式表现,不受环境条件和发育阶段的影响,标记的数目多、多态性高。有许多分子标记表现为共显性.能提供完整的遗传信息。分子标记可用于分子图谱构建、基因定位、DNA指纹库建立等。Helentiaris(1986)等用100多个500-1000bp的简单序列克隆建立了第一张玉米RFLP分子标记遗传图谱.定位于113个位点。到1995年玉米遗传连锁图已经定位了1 168个RFLP标记。根据DNA分子标记、可以准确定位玉米的各种质量性状和数量性状基因,使育种者可更清楚地了解一些重要性状的遗传基础,有助于根据基因间的互作效应,基因与标记间的遗传距离等。决定选用哪种育种方法.配制多少组合及培育多大供选群体,从而制定高效育种计划。1991年,Ottaviano、Reiter和Beavis分别应用RFLP技术,对控制玉米耐热性、低磷环境胁迫和株高3个性状进行了分子标记。到1996年.玉米的株高、穗位高、叶片数、叶面积、雄穗分枝数、吐丝期、抗倒性、抗旱性、穗长、穗粗、穗行数、百粒重、粒深、单株粒重、蛋白质含量、淀粉含量、油脂含量等主要数量性状,都已进行了标记。在辅助选择及杂种优势分析方面.近年来.许多育种者利用DNA分子标记提示的遗传多样性,计算自交系之间的遗传距离.并以此预测杂种优势。Ai- mone(1998)用一次能够标记200多个位点的AFLP技术.分析不同杂种优势群间13个自交系的遗传差异.发现特殊遗传距离与特殊配合力之间具有一定的相关性。Mumm(1994)等和Dubreuil(1996)等成功地利用RFLP标记对欧洲和北美的常用玉米自交系进行了杂种优势群划分。刘新芝等利用RAPD标记首次对我国玉米自交系进行杂种优势群划分。吴敏生(2000)等利用AFLP分子标记技术研究了17个玉米优良自交系的遗传多态性.李新海(2000)等利用SSR标记研究21个玉米自交系的遗传变异,他们的研究结果表明AFLP、SSR可用于玉米自交系遗传变异分析.并可用于杂种优势群划分.这为玉米分子标记辅助育种、选配杂种组合提供了理论依据。分子标记技术近年也已被成功用于玉米抗病虫遗传研究。
2基因工程在玉米遗传育种中的应用展望
2.1基因工程在玉米遗传育种中存在的问题
如前所述转基因中.抗虫的Bt基因潜在问题是害虫可能会产生抗性.解决方法是将遗传工程植株和非工程化植株混种.以保证在繁育群体中保留一部分未经筛选的害虫,或同时使用两种以上Bt基因转化农作物或联合使用Bt基因和其他类型的抗虫基因:CpTL基因要求能够在转基因植物中高效表达,给基因工程带来一定困难。解决这一问题的关键在于对表达的不同调控机理的深入研究上。利用植物凝集素基因进行玉米抗虫基因工程刚刚开始不久,获得的转基因植株是否对人、畜无害,还有待进一步研究证实。另外,广泛种植的转基因Bt花粉能够杀死一种蝴蝶。这种昆虫体表接触到Bt花粉之后.就会逐渐死亡。基因工程与环境关系方面的问题有待加强研究。另一方面,基因工程还存在基因转化率低的问题。目前,已获得的许多植物的转基因植株,实际上都是进行了大量的重复实验而得到的几个转化体克隆。玉米方面高频再生受体系统中的再生频率低,基因型依赖性强。组织培养水平也应随基因工程技术发展而需进一步提高。基因工程与常规育种的结合也应引起高度重视。我国在基因工程技术应用方面,由于财力所限和历史原因,起步较晚,与国际先进水平相比,有明显的差距。
2.2基因工程在玉米遗传育种中的应用展望
在饱和遗传图谱和分子标记的基础上,Pratt(1992)等开展了抗病基因分子标记辅助选择工作。尤其是QTLs的分子标记基因定位,使操作单个QTL成为可能。育种者可从单个主基因或单个QTL直接选择。在抗病基因和外壳蛋白基因克隆方面.利用转座子标记法已得到克隆的玉米抗圆斑病基因Hml、玉米的抗锈病基因RPI、玉米矮花叶病毒外壳蛋白基因相继被克隆。转基因玉米数量也是逐年增多。1998年转基因玉米在全球种植面积为830万hm2.1999年增至1100万hm2。油分含量高、加工品质好、营养丰富,是将来玉米转基因的研究方向。因而转基因研究应从单基因的转化向多基因转化方向发展。加强特种玉米的转基因研究。我国要加强国际间合作,充分利用我国的资源优势和现有成果,用不同的分子标记来实现我们自己的研究目的。利用分子标记.建立我国玉米自交系和杂交种遗传脆弱性监测机制及体系。通过研究遗传多样性,为玉米种质资源收集、保存和利用,为亲本选择、玉米类群的划分和组建提供依据。同时加强基因工程在杂种优势预测方面的研究。使基因工程更好地服务于玉米遗传育种工作。将基因工程与常规育种方法结合起来,可以准确地鉴定基因型。例如,可以先用常规方法把多个抗性基因组装在一起。然后利用分子标记技术快速、准确地鉴定出多抗性基因型。应用基因工程技术与常规育种方法紧密结合是玉米育种的一个突破方向。而实现种间、属间甚至动、植物间的基因流动是另一个突破方向。
目前,发展起来的基因芯片技术弥补了传统核酸印迹杂交技术复杂、自动化程度低、检测目标分子数量少、成本高、效率低等不足,已被广泛应用于基因表达研究、发现新基因等领域,将来有望在玉米遗传育种上发挥其重要作用。
5.算两次
对同一对象从两个不同角度去进行计数,再将两方面计算的结果综合起来,获得所需结论。这样一种处理问题的方法,称之为算两次。
在排列组合中,常对同一问题可有不同的分类办法去解,可得到有关排列数与组合数的不同关系式。
[例题解析]
例1 完成下列选择题与填空题
(1)有三个不同的信箱,今有四封不同的信欲投其中,则不同的投法有 种。
A.81 B.64 C.24 D.4
(2)四名学生争夺三项冠军,获得冠军的可能的种数是( )
A.81 B.64 C.24 D.4
(3)有四位学生参加三项不同的竞赛,
①每位学生必须参加一项竞赛,则有不同的参赛方法有 ;
②每项竞赛只许有一位学生参加,则有不同的参赛方法有 ;
③每位学生最多参加一项竞赛,每项竞赛只许有一位学生参加,则不同的参赛方法有 。
解析 (1)完成一件事是“分步”进行还是“分类”进行,是选用基本原理的关键。将“投四封信”这件事分四步完成,每投一封信作为一步,每步都有投入三个不同信箱的三种方法,因此:N=3×3×3×3=34=81,故答案选A。
本题也可以这样分类完成,①四封信投入一个信箱中,有C31种投法;②四封信投入两个信箱中,有C32(C41·A22+C42·C22)种投法;③四封信投入三个信箱,有两封信在同一信箱中,有C42·A33种投法、,故共有C31+C32(C41·A22+C42C22)+C42·A33=81(种)。故选A。
(2)因学生可同时夺得n项冠军,故学生可重复排列,将4名学生看作4个“店”,3项冠军看作“客”,每个“客”都可住进4家“店”中的任意一家,即每个“客”有4种住宿法。由分步计数原理得:N=4×4×4=64。
故答案选B。
(3)①学生可以选择项目,而竞赛项目对学生无条件限制,所以类似(1)可得
N=34=81(种);
②竞赛项目可以挑学生,而学生无选择项目的机会,每一项可以挑4种不同学生,共有
N=43=64(种);
③等价于从4个学生中挑选3个学生去参加三个项目的竞赛,每人参加一项,故共有
C43·A33=24(种)。
注 本题有许多形式,一般地都可以看作下列命题:
设集合A={a1,a2,…,an},集合B={b1,b2,…,bm},则f:A→B的不同映射是mn,f:B→A的不同映射是nm。
若n≤m,则f:A→B的单值映射是:Amn。
例2 同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则四张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
解法一 由于共四人(用1,2,3,4代表甲、乙、丙、丁四人),这个数目不大,化为填数问题之后,可用穷举法进行具体的填写:

再按照题目要求检验,最终易知有9种分配方法。
解法二 记四人为甲、乙、丙、丁,则甲送出的卡片可以且只可以由其他三人之一收到,故有3种分配方式;以乙收到为例,其他人收到卡片的情况可分为两类:
第一类:甲收到乙送出的卡片,这时丙、丁只有互送卡片1种分配方式;
第二类:甲收到的不是乙送出的卡片,这时,甲收到卡片的方式有2种(分别是丙和丁送出的)。对每一种情况,丙、丁收到卡片的方式只有一种。
因此,根据乘法原理,不同的分配方式数为 3×(1+2)=9。
解法三 给四个人编号:1,2,3,4,每个号码代表1个人,人与号码之间的关系为一对一的关系;每个人送出的贺年卡赋给与其编号相同的数字作为代表,这样,贺年卡的分配问题可抽象为如下“数学问题”:将数字1,2,3,4,填入标号为1,2,3,4的4个方格里,每格填写一个数字,且每个方格的编号与所填数字都不同的填法共有多少种(也可以说成:用数字1,2,3,4组成没有重复数字的4位数,而且每位数字都不等于位数的4位数共有多少个)?
这时,可用乘法原理求解答案:
首先,在第1号方格里填写数字,可填上2、3、4中的任一个数,有3种填法;
其次,当第1号方格填写的数字为i(2≤i≤4)时,则填写第i种方格的数字,有3种填法;
最后,将剩下的两个数填写到空着的两个空格里,只有1种填法(因为剩下的两个数中,至少有1个与空着的格子的序号相同)。
因此,根据乘法原理,得不同填法:
3×3×1=9
注 本题是“乱坐问题”,也称“错排问题”,当元素较大时,必须用容斥原理求解,但元素较小时,应用分步计数原理和分类计数原理便可以求解,或可以穷举。
例3 宿舍楼走廊上有有编号的照明灯一排8盏,为节约用电又不影响照明,要求同时熄掉其中3盏,但不能同时熄掉相邻的灯,问熄灯的方法有多少种?
解法一 我们将8盏灯依次编号为1,2,3,4,5,6,7,8。
在所熄的三盏灯中,若第一盏熄1号灯,第二盏熄3号灯,则第3盏可以熄5,6,7,8号灯中的任意一盏,共有4种熄法。
若第一盏熄1号灯,第2盏熄4号灯,则第3盏可以熄6,7,8号灯中的任意一盏。
依次类推,得若1号灯熄了,则共有4+3+2+1=10种熄法。
若1号灯不熄,第一盏熄的是2号灯,第二盏熄的是4号灯,则第三盏可以熄6,7,8号灯中的任意一盏,共有3种熄法。
依次类推得,若第一盏灯熄的是2号灯,则共有3+2+1=6种熄法。
同理,若第一盏熄的是3号灯,则共有2+1=3种熄法。
同理,若第一盏熄的是4号灯,则有1种熄法。
综上所述共有:10+6+3+1=20种熄法。
解法二 我们可以假定8盏灯还未安装,其中5盏灯是亮着的,3盏灯不亮。这样原问题就等价于:将5盏亮着的灯与3盏不亮的灯排成一排,使3盏不亮的灯不相邻(灯是相同的)。5盏亮着的灯之间产生6个间隔(包括两边),从中插入3个作为熄灭的灯--就是我们经常解决的“相邻不相邻”问题,采用“插入法”,得其答案为C63=20种。
注 解法一是穷举法,将所有可能的情况依次逐一排出。这种方法思路清晰,但有时较繁。方法二从另外一个角度审题,认清其数学本质,抽象成数学模型,解题时有一种豁然开朗的感觉。
例4 已知直线ax+by+c=0中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数。
解 设倾斜角为θ,
由θ为锐角,得tanθ=- >0,即a、b异号。
>0,即a、b异号。
(1)若c=0,a、b各有3种取法,排除2个重复(3x-3y=0,2x-2y=0,x-y=0),故有3×3-2=7(条)。
(2)若c≠0,a有3种取法,b有3种取法,而同时c还有4种取法,且其中任两条直线均不相同,故这样的直线有3×3×4=36条,从而符合要求的直线共有7+36=43条。
注 本题是1999年全国高中数学联赛中的一填空题,据抽样分析正确率只有0.37。错误原因没有对c=0与c≠0正确分类;没有考虑c=0中出现重复的直线。
例5 平面上给定10个点,任意三点不共线,由这10个点确定的直线中,无三条直线交于同一点(除原10点外),无两条直线互相平行。求:(1)这些直线所交成的点的个数(除原10点外)。(2)这些直线交成多少个三角形。
解法一 (1)由题设这10点所确定的直线是C102=45条。
这45条直线除原10点外无三条直线交于同一点,由任意两条直线交一个点,共有C452个交点。而在原来10点上有9条直线共点于此。所以,在原来点上有10C92点被重复计数。
所以这些直线交成新的点是:C452-10C92=630。
(2)这些直线所交成的三角形个数可如下求:因为每个三角形对应着三个顶点,这三个点来自上述630个点或原来的10个点。所以三角形的个数相当于从这640个点中任取三个点的组合,即C6403=43 486080(个)。
解法二 (1)如图对给定的10点中任取4个点,四点连成6条直线,这6条直线交3个新的点。故原题对应于在10个点中任取4点的不同取法的3倍,即这些直线新交成的点的个数是:3C104=630。

(2)同解法一。
注 用排列、组合解决有关几何计算问题,除了应用排列、组合的各种方法与对策之外,还要考虑实际几何意义。
例6 (1)如果(x+ )2n展开式中,第四项与第六项的系数相等。求n,并求展开式中的常数项;
)2n展开式中,第四项与第六项的系数相等。求n,并求展开式中的常数项;
(2)求( -
- )8展开式中的所有的有理项。
)8展开式中的所有的有理项。
解 (1)由C2n3=C2n5,可得3+5=2n
∴ n=4。
设第k+1项为常数项
则 Tk+1=C8k·x8-k·x-k=C8k·x8-2k
∴8-2k=0,即k=4
∴常数项为T5=C84=70。
(2)设第k+1项有理项,则

因为0≤k≤8,要使 ∈Z,只有使k分别取0,4,8
∈Z,只有使k分别取0,4,8
所以所求的有理项应为:
T1=x4,T5= x,T9=
x,T9= x-2
x-2
注 (1)二项式展开中,要注意“系数”与“二项式系数”的区别;
(2)在二项展开式中求得k后,对应的项应该是k+1项。
例7 (1)求4×6n+5n+1被20除后的余数;
(2)7n+Cn17n-1+Cn2·7n-2+…+Cnn-1×7除以9,得余数是多少?
(3)根据下列要求的精确度,求1.025的近似值。①精确到0.01;②精确到0.001。
解 (1)首先考虑4·6n+5n+1被4整除的余数。
∵5n+1=(4+1)n+1=4n+1+Cn+114n+Cn+124n-1+…+Cn+1n·4+1
∴其被4整除的余数为1
∴被20整除的余数可以为1,5,9,13,17
然后考虑4·6n+1+5n+1被5整除的余数。
∵4·6n=4·(5+1)n=4(5n+Cn1·5n-1+Cn2·5n-2+…+Cnn-1·5+1)
∴被5整除的余数为4
∴其被20整除的余数可以为4,9,14,19。
综上所述,被20整除后的余数为9。
(2) 7n+Cn1·7n-1+Cn2·7n-2+…+Cnn-1·7
=(7+1)n-1=8n-1=(9-1)n-1
=9n-Cn1·9n-1+Cn2·9n-2+…+(-1)n-1Cnn-1·9+(-1)nCnn-1
(i)当n为奇数时
原式=9n-Cn1·9n-1+Cn2·9n-2+…+(-1)n-1Cnn-1·9-2
∴除以9所得余数为7。
(ii)当n为偶数时
原式=9n-Cn1·9n-1+Cn2·9n-2+…+(-1)n-1Cnn-1·9
∴除以9所得余数为0,即被9整除。
(3)(1.02)5≈(1+0.02)5
=1+c51·0.02+C52·0.022+C53·0.023+C540.024+C55·0.025
∵C52×0.022=0.004,C53×0.023=8×10-5
∴①当精确到0.01时,只要展开式的前三项和,1+0.10+0.004=1.104,近似值为1.10。
②当精确到0.001时,只要取展开式的前四项和,1+0.10+0.004+0.0008=1.10408,近似值为1.104。
注 (1)用二项式定理来处理余数问题或整除问题时,通常把底数适当地拆成两项之和或之差再按二项式定理展开推得所求结论。
(2)用二项式定理来求近似值,可以根据不同精确度来确定应该取到展开式的第几项。
例8 证明下列不等式:
(1) ≥(
≥(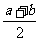 )n,(a、b∈{x|x是正实数},n∈N);
)n,(a、b∈{x|x是正实数},n∈N);
(2)已知a、b为正数,且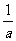 +
+ =1,则对于n∈N有
=1,则对于n∈N有
(a+b)n-an-bn≥22n-2n+1。
证明 (1)令a=x+δ, b=x-δ
则x=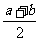
an+bn=(x+δ)n+(x-δ)n
=xn+Cn1xn-1δ+…+Cnnδn+xn-Cn1xn-1δ+…(-1)nCnnδn
=2(xn+Cn2xn-2δ2+Cn4xn-4δ4+…)
≥2xn
即 ≥(
≥(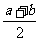 )n
)n
(2)(a+b)n=an+Cn1an-1b+…+Cnnbn
(a+b)n=bn+Cn1bn-1a+…+Cnnan
上述两式相加得:
2(a+b)n=(an+bn)+Cn1(an-1b+bn-1a)+…+Cnk(an-kbk+bn-kak)+…+Cnn(an+bn) (*)
∵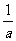 +
+ =1,且a、b为正数
=1,且a、b为正数
∴ab=a+b≥2 ∴ab≥4
∴ab≥4
又∵ an-kbk+bn-kak≥2 =2(
=2( )n(k=1,2,…,n-1)
)n(k=1,2,…,n-1)
∴2(a+b) n≥2an+2bn+Cn12( )n+Cn22(
)n+Cn22( )n+…+Cnn-12(
)n+…+Cnn-12( )n
)n
∴(a+b)n-an-bn
≥(Cn1+Cn2+…+Cnn-1)·( )n
)n
≥(2n-2)·2n
=22n-2n+1
注 利用二项式定理的展开式,可以证明一些与自然数有关的不等式问题。题(1)中的换元法称之为均值换元(对称换元)。这样消去δ奇数次项,从而使每一项均大于或等于零。题(2)中,由由称位置二项式系数相等,将展开式倒过来写再与原来的展开式相加,这样充分利用对称性来解题的方法是利用二项式展开式解题的常用方法。
例9 已知(1-ax)n展开式的第p,p+1,p+2三项的二项式系数构成等差数列,第n+1-p与第n+2-p项的系数之和为0,而(1-ax)n+1展开式的第p+1与p+2项的二项式系数之比为1∶2。
(1)求(1-ax)n+1展开式的中间项;
(2)求(1-ax)n的展开式中系数最大的项。
解 由题设得:

由①得,2Cnp= Cnp+
Cnp+ Cnp
Cnp
两边约去Cnp,可得:
2= +
+
由③得,2Cn+1p= Cn+1p
Cn+1p
约去Cn+1p可得,n=3p+1
解方程组
得:n=7,p=2.
将p=2,n=7代入②得:
C57(-a)5+C76·(-a)6=0
解之得:a=0或3。
若a=0 ,则(1-0·x)8的中间项T5=0,(1-0·x)7展开式中系数最大的项是T1=1。
若a=3,则(1-3x)8的中间项T5=C84·(-3x)4=5670x4,(1-3x)7的展开式中,奇数项系数为正,
令 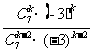 ≥1
≥1
解之得:k≤6。
故(1-3x)7展开式中系数最大的项为
T7=C76·(-3)6·x6=5103x6。
注 一般地,求(a+bx)n展开式中系数绝对值最大的项的方法是:
设第k+1项为系数绝对值最大的项,则由

求出k的取值范围,从而确定第几项最大。
例10 求证下列各式
(1)Cnk+Cnk-1=Cn+1k;
(2)Cn0Cmp+Cn1Cmp-1+…+CnpCm0=Cm+np。
证明 (1)对于给定的n+1个元素,从n+1个元素中任意选出k个元素的不同组合有Cn+1k。另一方面,设a是n+1个元素中的一个。对于a我们这样分类。
(i)若a不选,则在n个元素中选k个,有Cnk种不同的选法。
(ii)若a选,则在n个元素中再选k-1个,有Cnk-1种不同的选法。
故从n+1个元素中选k个元素组成一组的不种选法是:Cnk+Cnk-1。
所以,Cnk+Cnk-1=Cn+1k。
(2)仿(1)我们也用排列组合的知识来证明。事实上右边Cm+np,可看作下列命题:
从m个红球,n个白球中,任选p个球的不同选法是Cm+np种。
另一方面,我们按选红球的个数分类:(i)取p个红球,0个白球;(ii)取p-1个红球,1个白球,…,取0个红球,p个白球,这样的每类选法数为:Cn0Cmp,Cn1Cmp-1,…,CnpCm0
∴由分类计数原理可得:
Cn0Cmp+Cn1Cmp-1+…+CnpCm0=Cm+np
(2)另证:∵(1+x)n(1+x)m≡(1+x)m+n
左边展开式中xp的系数是:
Cn0Cmp+Cn1Cmp-1+…+CnpCm0
右边展开式中xp的系数是:Cm+np
由多项式恒等条件可知
Cn0Cmp+Cn1Cmp-1+…+CnpCm0=Cm+np
注 本题的证明方法称之为算两次,对一个数学模型从不同角度去解,得出两个结果,将这两个结果综合起来,得到我们所需证明的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com