
3.如图(a)所示,质量为m的小球放在光滑水平面上,在界限MN的左方始终收到水平恒力 作用,在MN的右方受
作用,在MN的右方受 外还受到与
外还受到与 在同一条直线上的水平恒力
在同一条直线上的水平恒力 的作用。小球从A点由静止开始运动,运动的
的作用。小球从A点由静止开始运动,运动的 图象如图(b)所示,由图可知下列中说法正确的是 ( )
图象如图(b)所示,由图可知下列中说法正确的是 ( )


A. 与
与 的比值大小为1:2 B.
的比值大小为1:2 B. 的大小为
的大小为
C. s时,小球经过界线MN D.
s时,小球经过界线MN D. s时,小球经过界线MN
s时,小球经过界线MN
2.如图所示,质量为M的物体,在与竖直方向成θ角、
大小为F的恒力作用下,沿竖直墙壁匀速下滑,物体
与墙壁间的动摩擦因数为μ,则无图收到摩擦力的大
小为 ( )
A.Mg-Fcosθ B.μ(Mg+Fcosθ)
C.μFsinθ D.μ(Mg-Fcosθ)
1. 小船横渡一条河,船本身提供的速度大小方向
小船横渡一条河,船本身提供的速度大小方向
都不 变。已知小船的运动轨迹如图所示,
则河水流速 ( )
A.越接近B岸水速越大
B.越接近B岸水速越小
C.由A到B水速先增后减
 D.水流速度恒定
D.水流速度恒定
22.已知函数 ,且
,且
(1) 试用含 的代数式表示b,并求
的代数式表示b,并求 的单调区间;
的单调区间;
(2)令 ,设函数
,设函数 在
在 处取得极值,记点M (
处取得极值,记点M ( ,
,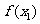 ),N(
),N( ,
, ),P(
),P( ),
),  ,请仔细观察曲线
,请仔细观察曲线 在点P处的切线与线段MP的位置变化趋势,并解答问题:若对任意的m
在点P处的切线与线段MP的位置变化趋势,并解答问题:若对任意的m  (
( , x
, x
 ,线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
,线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;

22 解法一:(Ⅰ)依题意,得
由 .
.
从而
令 21世纪教育网
21世纪教育网 

①当a>1时, 
当x变化时, 与
与 的变化情况如下表:
的变化情况如下表:
|
x |
 |
 |
 |
 |
+ |
- |
+ |
 |
单调递增 |
单调递减 |
单调递增 |
由此得,函数 的单调增区间为
的单调增区间为 和
和 ,单调减区间为
,单调减区间为 。
。
②当 时,
时, 此时有
此时有 恒成立,且仅在
恒成立,且仅在 处
处 ,故函数
,故函数 的单调增区间为R
的单调增区间为R
③当 时,
时, 同理可得,函数
同理可得,函数 的单调增区间为
的单调增区间为 和
和 ,单调减区间为
,单调减区间为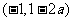 21世纪教育网
21世纪教育网 

综上:①当 时,函数
时,函数 的单调增区间为
的单调增区间为 和
和 ,单调减区间为
,单调减区间为 ;
;
②当 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
③当 时,函数
时,函数 的单调增区间为
的单调增区间为 和
和 ,单调减区间为
,单调减区间为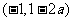 .
.
(Ⅱ)由 得
得 令
令 得
得
由(1)得 增区间为
增区间为 和
和 ,单调减区间为
,单调减区间为 ,所以函数
,所以函数 在处
在处 取得极值,故M(
取得极值,故M( )N(
)N( )。
)。
观察 的图象,有如下现象:
的图象,有如下现象:
①当m从-1(不含-1)变化到3时,线段MP的斜率与曲线 在点P处切线的斜率
在点P处切线的斜率 之差Kmp-
之差Kmp- 的值由正连续变为负。
的值由正连续变为负。
②线段MP与曲线是否有异于H,P的公共点与Kmp- 的m正负有着密切的关联;
的m正负有着密切的关联;
③Kmp- =0对应的位置可能是临界点,故推测:满足Kmp-
=0对应的位置可能是临界点,故推测:满足Kmp- 的m就是所求的t最小值,下面给出证明并确定的t最小值.曲线
的m就是所求的t最小值,下面给出证明并确定的t最小值.曲线 在点
在点 处的切线斜率
处的切线斜率 ;
;
线段MP的斜率Kmp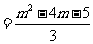 当Kmp-
当Kmp- =0时,解得
=0时,解得
直线MP的方程为 21世纪教育网
21世纪教育网 

令
当 时,
时, 在
在 上只有一个零点
上只有一个零点 ,可判断
,可判断 函数在
函数在 上单调递增,在
上单调递增,在 上单调递减,又
上单调递减,又 ,所以
,所以 在
在 上没有零点,即线段MP与曲线
上没有零点,即线段MP与曲线 没有异于M,P的公共点。
没有异于M,P的公共点。
当 时,
时, .
.
所以存在 使得
使得
即当 MP与曲线
MP与曲线 有异于M,P的公共点21世纪教育网
有异于M,P的公共点21世纪教育网 
 综上,t的最小值为2.
综上,t的最小值为2.
解法二:(1)同解法一.
(2)由 得
得 ,令
,令 ,得
,得
由(1)得的 单调增区间为
单调增区间为 和
和 ,单调减区间为
,单调减区间为 ,所以函数在处取得极值。故M(
,所以函数在处取得极值。故M( ).N(
).N( )
)
(Ⅰ) 直线MP的方程为
由
得
线段MP与曲线 有异于M,P的公共点等价于上述方程在(-1,m)上有根,即函数
有异于M,P的公共点等价于上述方程在(-1,m)上有根,即函数
 上有零点.
上有零点.
因为函数 为三次函数,所以
为三次函数,所以 至多有三个零点,两个极值点.
至多有三个零点,两个极值点.
又 .因此,
.因此,  在
在 上有零点等价于
上有零点等价于 在
在 内恰有一个极大值点和一个极小值点,即
内恰有一个极大值点和一个极小值点,即 内有两不相等的实数根.
内有两不相等的实数根.
等价于 即
即
又因为 ,所以m 的取值范围为(2,3)
,所以m 的取值范围为(2,3)
当 时,
时, .
.
所以存在 使得
使得
即当 MP与曲线
MP与曲线 有异于M,P的公共点21世纪教育网
有异于M,P的公共点21世纪教育网 

综上,t的最小值为2.
21. 设f(x)=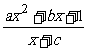 (a>0)为奇函数,且 |f(x)|min=2
(a>0)为奇函数,且 |f(x)|min=2 ,数列{an}与{bn}满足如下关系:
,数列{an}与{bn}满足如下关系:
a1=2,an+1= .
.
(1)求f(x)的解析表达式;
(2)证明:当n∈N+时,有bn≤( )n.
)n.
20.解:(1)m+n=(cosθ-sinθ+ ,cosθ+sinθ),
,cosθ+sinθ),
|m+n|=
=
=
=2
∵θ∈[π,2π],∴ ,∴cos(θ+
,∴cos(θ+ )≤1,|m+n|max=2
)≤1,|m+n|max=2 .
.
(2)由已知|m+n|= ,得cos(θ+
,得cos(θ+ )=
)= .
.
又cos(θ+ )=2cos2(
)=2cos2( )-1,∴cos2(
)-1,∴cos2( )=
)= ,
,
∵θ∈[π,2π],∴ ,∴cos(
,∴cos(
20.已知向量m=(cosθ,sinθ)和n=( -sinθ,cosθ),θ∈[π,2π].
-sinθ,cosθ),θ∈[π,2π].
(1)求|m+n|的最大值;
(2)当|m+n|= 时,求cos(
时,求cos( )的值.
)的值.
19.解:(1)设“取出的2个球颜色相同”为事件A
P(A)= 4(分)
4(分)
(2)
|
ξ |
0 |
1 |
2 |
|
P |
 |
 |
 |
7(分)
Eξ=0× +1×
+1× +2×
+2× =
= 9分
9分
(3)设“取出的2个球中颜色不相同”为事件B,则
P(B)=  11分
11分
∴x2-6x+2>0
∴x>3+ 或x<3-
或x<3- ,x的最小值为6. 14分
,x的最小值为6. 14分
19.(本小题满分14分)
一袋中有m(m∈N*)个红球,3个黑球和2个白球,现从中任取2个球.
(Ⅰ)当m=4时,求取出的2个球颜色相同的概率;
(Ⅱ)当m=3时,设ξ表示取出的2个球中黑球的个数,求ξ的概率分布及数学期望;
(Ⅲ)如果取出的2个球颜色不相同的概率小于 ,求m的最小值.
,求m的最小值.
18. [解析](I)∵ 为锐角,
为锐角,
∴ 

∵ 
∴  …………………………………………7分
…………………………………………7分
(II)由(I)知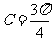 ,∴
,∴ 
由 得
得
 ,即
,即
又∵ 
∴  ∴
∴ 
∴  …………………………………………14分
…………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com