
32.(2009江苏卷) 设向量
(1)若 与
与 垂直,求
垂直,求 的值;
的值;

(2)求 的最大值;
的最大值;
(3)若 ,求证:
,求证: ∥
∥ .
. 
[解析] 本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明得基本能力。满分14分。

31.(2009北京理)(本小题共13分)
在 中,角
中,角 的对边分别为
的对边分别为 ,
, 。
。
(Ⅰ)求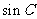 的值;
的值;
(Ⅱ)求 的面积.
的面积.
解析 本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,主要考查基本运算能力.
解(Ⅰ)∵A、B、C为△ABC的内角,且 ,
,
∴ ,
,
∴ .
.
(Ⅱ)由(Ⅰ)知 ,
,
又∵ ,∴在△ABC中,由正弦定理,
,∴在△ABC中,由正弦定理,
∴ .
.
∴△ABC的面积
30.(2009北京文)(本小题共12分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
解析 本题主要考查特殊角三角函数值、诱导公式、二倍角的正弦、三角函数在闭区间上的最值等基础知识,主要考查基本运算能力.
解(Ⅰ)∵ ,
,
∴函数 的最小正周期为
的最小正周期为 .
.
(Ⅱ)由 ,∴
,∴ ,
,
∴ 在区间
在区间 上的最大值为1,最小值为
上的最大值为1,最小值为 .
.
29.(2009全国卷Ⅰ理)在 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、 ,已知
,已知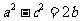 ,且
,且 求b
求b 

分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1)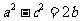 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)
左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)  过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解法一:在 中
中 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有: 化简并整理得:
化简并整理得: .又由已知
.又由已知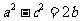
 .解得
.解得 .
. 

解法二:由余弦定理得:  .又
.又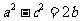 ,
, 。
。
所以 …………………………………①
…………………………………①
又 ,
,
 ,即
,即
由正弦定理得 ,故
,故 ………………………②
………………………②
由①,②解得 。
。
评析:从08年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒:两纲中明确不再考的知识和方法了解就行,不必强化训练。
28.(2009辽宁卷文)已知函数 的图象如图所示,
的图象如图所示,


则 =
=

解析 由图象可得最小正周期为
∴T= Þ ω=
答案 
27.(2009上海卷文)函数 的最小值是
。
的最小值是
。
答案 
解析  ,所以最小值为:
,所以最小值为:
26.(2009年上海卷理)已知函数 .项数为27的等差数列
.项数为27的等差数列 满足
满足 ,且公差
,且公差 .若
.若 ,则当
,则当 =____________是,
=____________是, .
.
答案 14
解析 函数 在
在
 是增函数,显然又为奇函数,函数图象关于原点对称,因为
是增函数,显然又为奇函数,函数图象关于原点对称,因为 ,
,
所以 ,所以当
,所以当 时,
时, .
.
25.(2009年上海卷理)当 ,不等式
,不等式 成立,则实数
成立,则实数 的取值范围是_______________.
的取值范围是_______________.
答案 k≤1
 解析 作出
解析 作出 与
与 的图象,要使不等式
的图象,要使不等式 成立,由图可知须k≤1
成立,由图可知须k≤1
24.(2009年上海卷理)函数 的最小值是_____________________ .
的最小值是_____________________ .
答案 
解析  ,所以最小值为:
,所以最小值为:
23.(2009湖南卷理)若x∈(0,  )则2tanx+tan(
)则2tanx+tan( -x)的最小值为
-x)的最小值为 

答案 
解析 由 ,知
,知 所以
所以 当且仅当
当且仅当 时取等号,即最小值是
时取等号,即最小值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com