
6.已知某射击运动员,每次击中目标的概率都是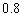 .现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,表示没有击中目标,2,3,4,5,6,,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
.现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,表示没有击中目标,2,3,4,5,6,,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5727 0293 7140 9857 0347 4373 8636 9647 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 6710 4281
据此估计,该射击运动员射击4次至少击中3次的概率为
A.0.85 B.0.8192 C.0.8 D. 0.75
5.下列函数 中,满足 “对
中,满足 “对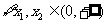 ,当
,当 时,都有
时,都有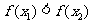 ”的是
”的是
A.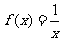 B.
B.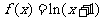 C.
C.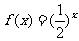 D.
D.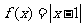
4.下列命题不正确的是
A.如果一个平面内的一条直线垂直于另一个平面内的任意直线,则两平面垂直;
B.如果一个平面内的任一条直线都平行于另一个平面,则两平面平行;
C.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;
D.如果两条不同的直线在一平面内的射影互相垂直,则这两条直线垂直.
3.已知双曲线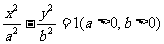 的离心率为
的离心率为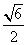 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
A. B.
B.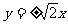 C.
C.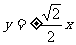 D.
D.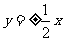
2.已知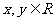 ,则“
,则“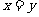 ”是“
”是“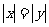 ”的
”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
1.设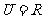 ,
, 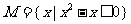 ,函数
,函数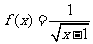 的定义域为
的定义域为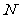 ,则
,则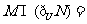
A.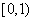 B.
B.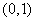 C.
C.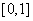 D.
D.
5. 在△ABC中,角A、B、C的对边分别为a、b、c,若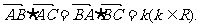
(Ⅰ)判断△ABC的形状; (Ⅱ)若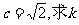 的值.
的值.
解:(I)
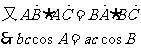
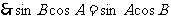
即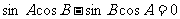
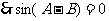
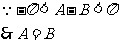
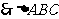 为等腰三角形.
为等腰三角形.
(II) 由(I)知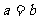
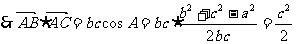

4.(2008年成都名校联盟高考数学冲刺预测卷二)在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(Ⅰ)求角B的大小;
|
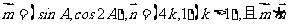 的最大值是5,求k的值.
的最大值是5,求k的值.
解:(I)∵(2a-c)cosB=bcosC,
∴(2sinA-sinC)cosB=sinBcosC
即2sinAcosB=sinBcosC+sinCcosB
=sin(B+C)
∵A+B+C=π,∴2sinAcosB=sinA
∵0<A<π,∴sinA≠0.
∴cosB=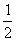
∵0<B<π,∴B=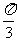
(II)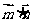 =4ksinA+cos2A
=4ksinA+cos2A
=-2sin2A+4ksinA+1,A∈(0,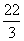 )
)
设sinA=t,则t∈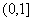 .
.
则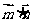 =-2t2+4kt+1=-2(t-k)2+1+2k2,t∈
=-2t2+4kt+1=-2(t-k)2+1+2k2,t∈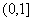
∵k>1,∴t=1时,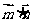 取最大值.
取最大值.
依题意得,-2+4k+1=5,∴k=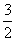
3.(江苏省滨海县08届高三第三次联考数学试卷)在 中,
中,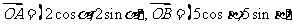 ,若
,若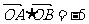 ,
则
,
则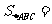 .
.
答案 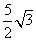
2.(2007届高三数学二轮复习新型题专题训练)已知 中
,角A,B,C的对边分别为a,b,c,AH为BC边上有高,以下结论:①
中
,角A,B,C的对边分别为a,b,c,AH为BC边上有高,以下结论:① ;②
;②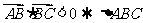 为锐角三角形③
为锐角三角形③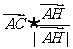
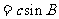 ;④
;④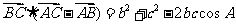 ,其中正确的个数是
,其中正确的个数是
A.1 B.2 C.3 D.4
答案 B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com