
21.(本题满分14分)
已知数列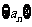 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求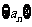 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
2010年佛山市普通高中高三教学质量检测(一)
20.(本题满分14分)
已知点 (
( ),过点
),过点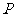 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为 、
、 (其中
(其中 ).
).
(Ⅰ)求 与
与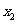 的值(用
的值(用 表示);
表示);
(Ⅱ)若以点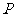 为圆心的圆
为圆心的圆 与直线
与直线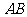 相切,求圆
相切,求圆 面积的最小值.
面积的最小值.
19.(本题满分14分)
某学校拟建一座长 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费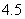 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
18.(本题满分14分)
 如图所示的长方体
如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: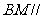 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
17.(本题满分12分)
 某校从参加高一年级期中考试的学生中随机抽出
某校从参加高一年级期中考试的学生中随机抽出 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个
内的频率,并补全这个
频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组
区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中随机抽取
名学生中随机抽取 人,抽到
人,抽到
的学生成绩在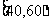 记
记 分,在
分,在 记
记 分,
分,
在 记
记 分,用
分,用 表示抽取结束后的总记分,
表示抽取结束后的总记分,
求 的分布列和数学期望.
的分布列和数学期望.
16.(本题满分12分)
已知向量 ,
, .向量
.向量 ,
, ,
,
且
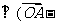
 .
.
(Ⅰ) 求向量 ;
;
(Ⅱ) 若 ,
, ,求
,求 的值.
的值.
(二)选做题(14-15题,考生只能从中选做一题,两题都做记第一题的得分)
14.(坐标系与参数方程)在平面直角坐标系下,曲线
 (
( 为参数),
为参数),
 曲线
曲线
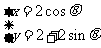 (
( 为参数).若曲线
为参数).若曲线 、
、 有公共点,
有公共点,
则实数 的取值范围____________.
的取值范围____________.
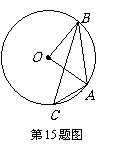
15.(几何证明选讲)如图,点 是圆
是圆 上的点,
上的点,
且 ,则
,则 对应的劣弧长为 .
对应的劣弧长为 .
 (一)必做题(9-13题)
(一)必做题(9-13题)
9. 复数 的值是
.
的值是
.
10.若数列 满足:
满足: ,
,
其前 项和为
项和为 ,则
,则 .
.
11.如图的算法流程图,若输入 ,
,
则运行程序输出的结果为 .
12.若对于任意实数 ,有
,有
 ,
,
则 的值为__________.
的值为__________.
13.将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥
的侧面和底面分别叫直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.
已知直角三角形具有性质:“斜边的中线长等于斜边边长的一半”.仿照此性质写出直角三棱锥具有的性质: .
8.佛山某家电企业要将刚刚生产的100台变频空调送往市内某商场,现有4辆甲型货车和8辆乙型货车可供调配。每辆甲型货车的运输费用是400元,可装空调20台,每辆乙型货车的运输费用是300元,可装空调10台,若每辆车至多运一次,则企业所花的最少运费为
A.2000元 B.2200元 C.2400元 D.2800元
7. 函数
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图像,则只要将
的图像,则只要将 的图像
的图像
A.向右平移 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度
C.向左平移 个单位长度 D.向左平移
个单位长度 D.向左平移 个单位长度
个单位长度
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com