
8.(2009山东卷文)已知定义在R上的奇函数 ,满足
,满足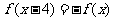 ,且在区间[0,2]上是增函数,则 ( ).
,且在区间[0,2]上是增函数,则 ( ).
A.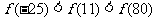 B.
B. 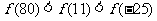
C. 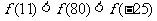 D.
D.
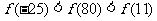
答案 D
解析 因为 满足
满足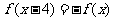 ,所以
,所以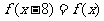 ,所以函数是以8为周期的周期函数, 则
,所以函数是以8为周期的周期函数, 则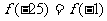 ,
,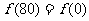 ,
,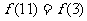 ,又因为
,又因为 在R上是奇函数,
在R上是奇函数,
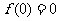 ,得
,得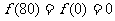 ,
,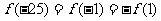 ,而由
,而由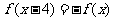 得
得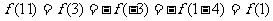 ,又因为
,又因为 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以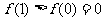 ,所以
,所以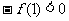 ,即
,即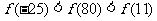 ,故选D.
,故选D.
[命题立意]:本题综合考查了函数的奇偶性、单调性、周期性等性质,运用化归的数学思想和数形结合的思想解答问题.
7. (2009山东卷文)定义在R上的函数f(x)满足f(x)= 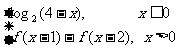 ,
,
则f(3)的值为 ( )
A.-1 B. -2 C.1 D. 2
答案 B
解析 由已知得 ,
,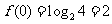 ,
,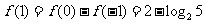 ,
,
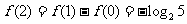 ,
,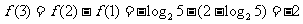 ,故选B.
,故选B.
[命题立意]:本题考查对数函数的运算以及推理过程.
6.(2009山东卷文)函数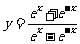 的图像大致为( ).
的图像大致为( ).
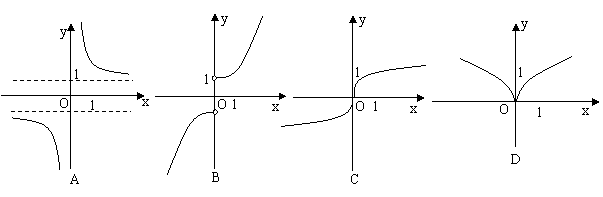

答案 A.
解析 函数有意义,需使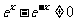 ,其定义域为
,其定义域为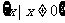 ,排除C,D,又因为
,排除C,D,又因为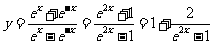 ,所以当
,所以当 时函数为减函数,故选A.
时函数为减函数,故选A.
[命题立意]:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
5.(2009山东卷理)定义在R上的函数f(x)满足f(x)= 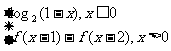 ,
,
则f(2009)的值为 ( )
A.-1 B. 0 C.1 D. 2
答案 C
解析 由已知得 ,
,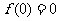 ,
, ,
,
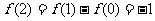 ,
,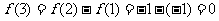 ,
,
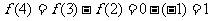 ,
,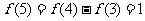 ,
,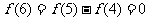 ,
,
所以函数f(x)的值以6为周期重复性出现.,所以f(2009)= f(5)=1,故选C.
[命题立意]:本题考查归纳推理以及函数的周期性和对数的运算.
4.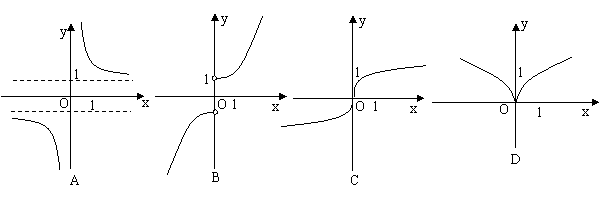 (2009山东卷理)函数
(2009山东卷理)函数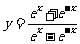 的图像大致为 ( ).
的图像大致为 ( ).
答案 A
解析 函数有意义,需使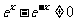 ,其定义域为
,其定义域为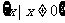 ,排除C,D,又因为
,排除C,D,又因为 ,所以当
,所以当 时函数为减函数,故选A.
时函数为减函数,故选A.
[命题立意]:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
3.(2009浙江文)若函数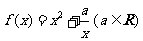 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ,
, 在
在 上是增函数
上是增函数
B. ,
, 在
在 上是减函数
上是减函数
C.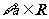 ,
, 是偶函数
是偶函数
D.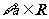 ,
, 是奇函数
是奇函数
答案 C
[命题意图]此题主要考查了全称量词与存在量词的概念和基础知识,通过对量词的考查结合函数的性质进行了交汇设问.
解析 对于 时有
时有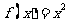 是一个偶函数
是一个偶函数
2.(2009浙江理)对于正实数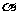 ,记
,记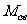 为满足下述条件的函数
为满足下述条件的函数 构成的集合:
构成的集合: 且
且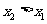 ,有
,有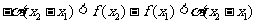 .下列结论中正确的是 ( )
.下列结论中正确的是 ( )
A.若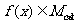 ,
,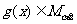 ,则
,则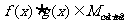
B.若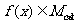 ,
,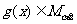 ,且
,且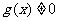 ,则
,则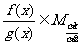
C.若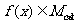 ,
,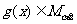 ,则
,则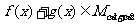
D.若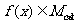 ,
,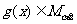 ,且
,且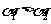 ,则
,则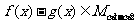
答案 C
解析 对于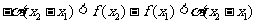 ,即有
,即有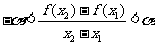 ,令
,令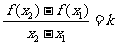 ,有
,有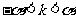 ,不妨设
,不妨设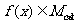 ,
,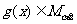 ,即有
,即有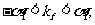
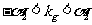 ,因此有
,因此有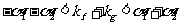 ,因此有
,因此有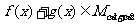 .
.
2009年高考题
1.(2009全国卷Ⅰ理)函数 的定义域为R,若
的定义域为R,若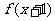 与
与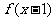 都是奇函数,则( )
都是奇函数,则( )
A. 是偶函数 B.
是偶函数 B. 是奇函数
是奇函数
C. D.
D.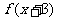 是奇函数
是奇函数
答案 D
解析 
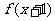 与
与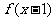 都是奇函数,
都是奇函数,
 ,
,
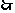 函数
函数 关于点
关于点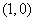 ,及点
,及点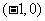 对称,函数
对称,函数 是周期
是周期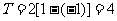 的周期函数.
的周期函数.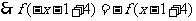 ,
, ,即
,即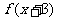 是奇函数。故选D
是奇函数。故选D
16.(2007-2008年吉林质检与邯郸一模改编)设命题P:关于x的不等式ax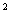 -ax-2a
-ax-2a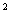 >1(a>0且a≠1)的解集为{x|-a<x<2a};命题Q:y=lg(ax2-x+a)的定义域为R。如果P或Q为真,P且Q为假,求a的取值范围
>1(a>0且a≠1)的解集为{x|-a<x<2a};命题Q:y=lg(ax2-x+a)的定义域为R。如果P或Q为真,P且Q为假,求a的取值范围
简解:P:0<a<1;Q:a>1/2;P、Q中有且仅有一个为真∴0<a≤1/2或a≥1
15.(广东地区2008年01月份期末试题)某医疗研究所为了检验某种血清预防感冒的作用,把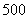 名使用血清的人与另外
名使用血清的人与另外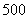 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设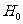 :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用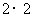 列联表计算得
列联表计算得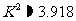 ,经查对临界值表知
,经查对临界值表知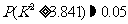 .
.
对此,四名同学做出了以下的判断:
p:有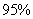 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用”
q:若某人未使用该血清,那么他在一年中有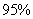 的可能性得感冒
的可能性得感冒
r:这种血清预防感冒的有效率为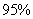
s:这种血清预防感冒的有效率为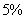
则下列结论中,正确结论的序号是 .(把你认为正确的命题序号都填上)
(1) p∧﹁q ; (2)﹁p∧q ;
(3)(﹁p∧﹁q)∧(r∨s); (4)(p∨﹁r)∧(﹁q∨s)
解析:(1)(4).本题考查了独立性检验的基本思想及常用逻辑用语.由题意,得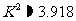 ,
,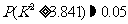 ,所以,只有第一位同学的判断正确,即:有
,所以,只有第一位同学的判断正确,即:有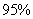 的把握认为“这种血清能起到预防感冒的作用”.由真值表知(1)(4)为真命题.
的把握认为“这种血清能起到预防感冒的作用”.由真值表知(1)(4)为真命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com