
9.(2006年安徽卷)函数 对于任意实数
对于任意实数 满足条件
满足条件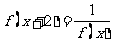 ,若
,若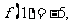 则
则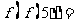 _______________。
_______________。
答案 -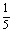
解析 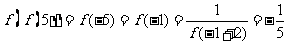 。
。
8.(2007年上海)函数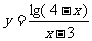 的定义域是
.
的定义域是
.
答案 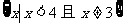
7.(2007上海春季5)设函数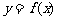 是奇函数. 若
是奇函数. 若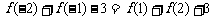
则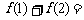 .
.
答案 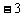
6.(2005年上海13)若函数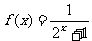 ,则该函数在
,则该函数在 上是 ( )
上是 ( )
A.单调递减;无最小值 B.单调递减;有最小值
C.单调递增;无最大值 D.单调递增;有最大值
答案 A
5.(07安徽)图中的图象所表示的函数的解析式为 ( )
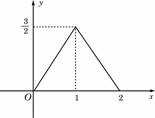 A.
A.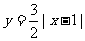 (0≤x≤2)
(0≤x≤2)
B.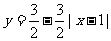 (0≤x≤2)
(0≤x≤2)
C. (0≤x≤2)
(0≤x≤2)
D.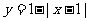 (0≤x≤2)
(0≤x≤2)
答案 B
4.(07重庆)已知定义域为R的函数 在区间
在区间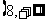 上为减函数,且函数
上为减函数,且函数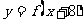 为偶函数,则 (
)
为偶函数,则 (
)
A. B.
B. 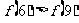
C.
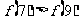 D.
D. 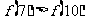
答案 D
3. (07福建)已知函数 为R上的减函数,则满足
为R上的减函数,则满足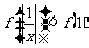 的实数
的实数 的取值范围
的取值范围
是 ( )
A. B.
B.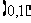
C. D.
D.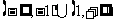
答案 C
2.(07天津)在 上定义的函数
上定义的函数 是偶函数,且
是偶函数,且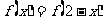 ,若
,若 在区间
在区间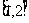 是减函数,则函数
是减函数,则函数 ( )
( )
A.在区间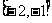 上是增函数,区间
上是增函数,区间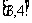 上是增函数
上是增函数
B.在区间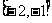 上是增函数,区间
上是增函数,区间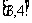 上是减函数
上是减函数
C.在区间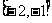 上是减函数,区间
上是减函数,区间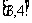 上是增函数
上是增函数
D.在区间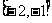 上是减函数,区间
上是减函数,区间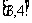 上是减函数
上是减函数
答案 B
1.(2008年山东文科卷)设函数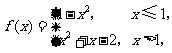 则
则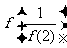 的值为(
)
的值为(
)
A.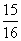 B.
B.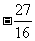 C.
C.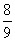 D.
D.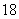
答案 A
50.(2009年上海卷理)已知函数 的反函数。定义:若对给定的实数
的反函数。定义:若对给定的实数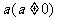 ,函数
,函数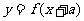 与
与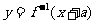 互为反函数,则称
互为反函数,则称 满足“
满足“ 和性质”;若函数
和性质”;若函数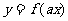 与
与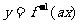 互为反函数,则称
互为反函数,则称 满足“
满足“ 积性质”。
积性质”。
(1)
判断函数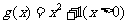 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2) 求所有满足“2和性质”的一次函数;
(3)
设函数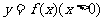 对任何
对任何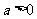 ,满足“
,满足“ 积性质”。求
积性质”。求 的表达式。
的表达式。
解 (1)函数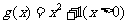 的反函数是
的反函数是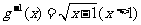
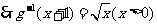
而 其反函数为
其反函数为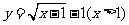
故函数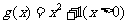 不满足“1和性质”
不满足“1和性质”
(2)设函数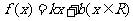 满足“2和性质”,
满足“2和性质”,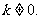
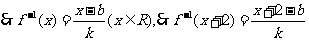 …….6分
…….6分
而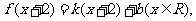 得反函数
得反函数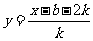 ………….8分
………….8分
由“2和性质”定义可知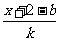 =
=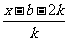 对
对 恒成立
恒成立
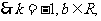 即所求一次函数为
即所求一次函数为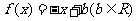 ………..10分
………..10分
(3)设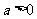 ,
,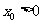 ,且点
,且点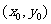 在
在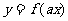 图像上,则
图像上,则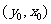 在函数
在函数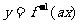 图象上,
图象上,
故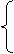
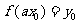 ,可得
,可得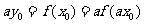 ,
......12分
,
......12分
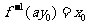
令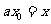 ,则
,则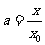 。
。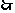
 ,即
,即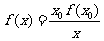 。 ......14分
。 ......14分
综上所述,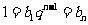
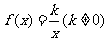 ,此时
,此时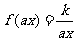 ,其反函数就是
,其反函数就是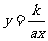 ,
,
而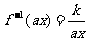 ,故
,故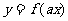 与
与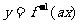 互为反函数 。
互为反函数 。
2005-2008年高考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com